あみだくじの当たりの分布 : 統計学が最強の学問である

西内啓「統計学が最強の学問である」ダイヤモンド社(2013/1)．変なタイトルの本なので図書館で借りてみた．

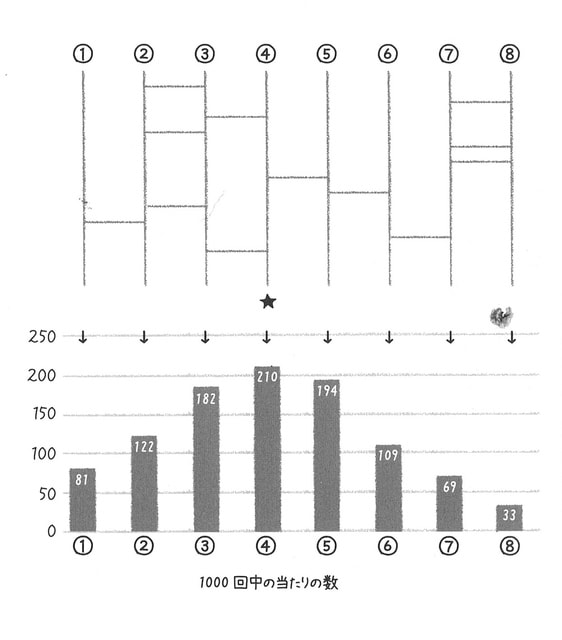
3 ページ，ほとんど冒頭にあみだくじ必勝法が出ている．縦線を (この場合は) ８本引き，当たりに星印をつける．その後 12 本の横線をでたらめに引く．これを 1000 回繰り返すと，縦線毎の当たりの分布は正規分布に近くなる．統計学さえ知っていればあみだくじは有利に引くことができる，というイントロ．

これは「どこが当たりか」がわかっていれば，その当たりに直結している線を選べ，と言っているに過ぎない．どこが当たりか分からなければ統計学は無力である．たとえば右端が当たりで，それを隠して試行すれば，４を選んだら外れる確率が大きい．
普通は下の方を折り返して，どこが当たりか分からないようにして，横線を引くことを始めるのではないか．

あみだくじの横線は，縦線の行き先を 1:1 で交換するに過ぎない．この本の実験が言っているのは，８本の縦線に対して 12 本の横線では本数が少な過ぎて，十分に交換が行われず，最初の設定が履歴として残るということだろう．
「あみだくじには何本の横線が必要か」という問題には発展しそうだが，統計学が最強の学問であることを証明してはいない．

本そのものについては，読了してから...


追記
ネットを漁ったら，同じように考える方が，横線の数を変えて当たり分布をシミュレーションで求めておられた．
Minkyのよもやま日記 あみだくじは公平か？ - 『統計学が最強の学問である』より http://skellington.blog.so-net.ne.jp/2013-07-10である．

Minky さんの結論は*****
- 線を引く本数が少ない場合は、当たりと同じ線上に線を引くというのがよさそうである。
- 線を引く本数が多くなっていった場合、一様分布に近づくので、スタート地点に関係なくなる。
- とはいえ、あみだくじで線を引くのって、せいぜい1本か2本であり、100本も線を引いたりしない。
- となると、当たりがどこにあるのか知っているのと知っていないのでは、公平性に大きく差があるという結果になる。

我が意を得たり !!