惑星とディスクの相互作用からの太陽系外惑星の傾斜の生成

原始惑星系円盤のガス消散とマイグレーションのタイミングが合うと自転軸が傾く場合もある。以下、機械翻訳。
コロンボのトップのダイナミクス：惑星とディスクの相互作用からの太陽系外惑星の傾斜の生成
2020年4月29日に提出
大規模な惑星の自転公転の不整合（傾斜）は、惑星の大気循環と潮汐加熱に強く影響する可能性があります。傾斜を生成するための有望な手段は、自転公転共鳴を経由することです。そこでは、システムが時間とともに進化するにつれて、惑星の自転と公転の歳差運動周波数が互いに交差します。そのようなメカニズムの1つは、内部惑星の軌道歳差運動を駆動する散逸（質量損失）原始惑星系ディスクを含みます。このシナリオでは、このシナリオを分析的に調査し、一般的な初期スピン方向と最終的な傾斜との間のマッピングを取得します。私たちは、（i）断熱進化（すなわち、ディスクが十分に遅い速度で消散する）の下で、初期のスピン方向の関数としての最終的な惑星の傾斜が、共鳴との相互作用によって支配される別個のトラックに分岐することを示します。（ii）非断熱進化の下では、広範囲の傾斜が励起されます。パラメータ空間のさまざまなレジームの最終的な傾斜の分析式を取得します。この論文で研究された動的システムは「コロンボのトップ」の例であり、私たちの分析と結果は他のアプリケーションに適合させることができます。

図1.カッシーニ状態の構成における角度の定義と、伝統的に採用されているθの記号の規則。


図2.ηの関数としてのカッシーニ状態の傾斜
Ｉ= 5°
。 細い縦の破線はηc（= 0.766　Ｉ= 5°）、CS1とCS4がマージして消滅し、
細い水平の破線は、θ= IおよびI − 180°を示します、ηηcのCS 2および3の漸近値。


図3. Hのレベル曲線（φ、cosθ）[Eq。 （15）] I = 5°の場合、暖かい色はより正の値を示します。 黒の固体
lineはセパラトリクスで、η＜ηc= 0.766の場合にのみ存在します。 3つのゾーン（I、II、III）は、セパラトリックスで分割され、ラベルが付けられています。
カッシーニの状態は、塗りつぶされた円で示され、図2と同じ色になります。セパラトリックスの内部、影付き
灰色で、正式にはη＜ηcに対してのみ定義されますが、進化したときにゾーンIIに流れ込むフェーズ空間のポイントを特定できます
時間的に先に進む（ηを断熱的に減少させる）; これは、パネル（a）の影付きの領域で、黒い点線で囲まれています。


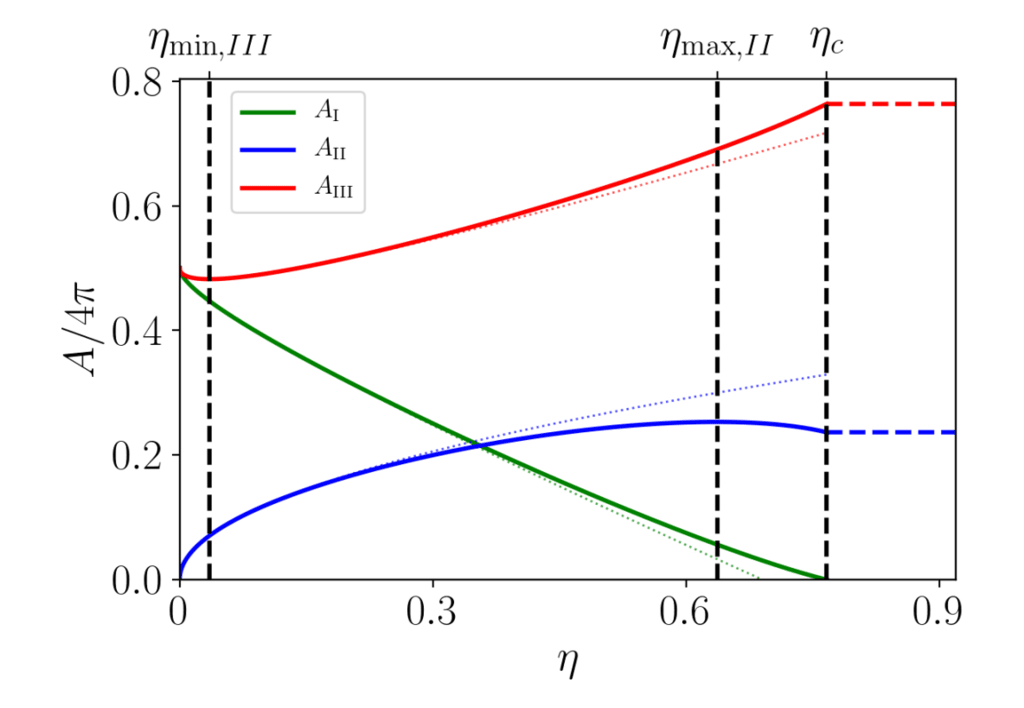
図4.実線は、それぞれの部分領域を示しています
ゾーンのＡＩ（η）/4πは、方程式によって与えられます。 （17）。 着色された
点線は、で使用される小さなη近似に対応しています
付録B.η＞ηcの色付きの破線はη＞ηcのAII、AIIIの有効値。ポイントを示します
それは、断熱的な減少の下でどちらかの領域に流れ込むでしょう
η＞ηc（本文を参照）。 縦の黒い破線η=ηc[式（14）]に対応し、ηの値
AIIが最大化され（ηmax、II）、AIIIが最小化される（ηmin、III、式（30））。

5.まとめ
この論文では、重力相互作用による惑星の傾斜の励起を研究しました。
外部、消散（質量損失）原始惑星系ディスク。
システムが通過するときに斜めの興奮が発生します
スピン歳差運動と軌道の間の永年の共鳴
（節点）歳差運動。このシナリオは最近、Millholland＆Batygin（2019）によって研究されました。
小さな初期の不確実性の特別な場合。対照的に、
このホワイトペーパーでは、任意の初期位置ずれ角度を考慮します。
コア降着は、広範囲の初期スピンにつながる可能性があります
オリエンテーション。結果をマッピングとして表示します
θsd、iからθf、ここでθsd、i初期の位置ずれ角度です
惑星の回転軸と円盤の軌道の間　角運動量軸、およびθf最後の惑星です
傾倒。両方の断熱におけるこのマッピングの動作をキャプチャする分析結果を導出しました
および非断熱限界：1.断熱限界（つまり、ディスクがaで散逸する）十分に遅いレート）、既知の結果を再現θf '90°
θsd、i '0の場合。（数値計算と分析引数を使用して）
非ゼロのθsd、iに対するθfの2値の動作（参照
図5）。正確に両方を分析的に計算します　最終的なθf値と達成の確率
断熱的不変性とセパラトリックス交差ダイナミクスの注意深い計算による各値。
2.ディスクがより速く消散するにつれて、断熱
条件[式（21）]が故障した場合、
広範囲の最終的な不確実性に到達することができます
与えられたθsd、i（図16を参照）。私たちは分析を提供します
θfの境界の式
式で（41）。
セクション1で述べたように、このホワイトペーパーでは、惑星とディスクの相互作用から惑星の傾斜を生成/変更する特定のシナリオを検討しましたが、動的問題はより一般的です（コロンボ
1966; Peale 1969、1974;ワード1975; Henrard＆Murigande 1987）。私たちの仕事はこれらの以前の仕事を超えています
進化への最も一般的な解決策を提供します
システムが「弱い」から進化するにつれて、「コロンボのトップ」の
スピン軌道カップリング」レジーム（η1）から「強いスピン軌道カップリング」レジーム（η1）へ。新しい分析
この論文で提示された結果は、他の
アプリケーション。