
🌬️🪞🌊 0 乗 : 是央 ゼオ 乗 : ゼロ 乗 🌙
;
解放🎵 を急ぐべき、 シナ⚡ による、
桜木 琢磨 市議 らをの 実質 での 拉致⚡ たる 事件ら⚡
;
🦋⛲ 日本医学 ; 和法🎵
三石分子栄養学 ➕ 藤川徳美院長系 ; 代謝医学❗
;
人々の体らの各々の、
構造らや、 機能ら
、 が、
その遺伝子らも含まれてある、
細胞ごとにおいて、
色々な アミノ酸 たちから
特定の、
タンパク質 ✔️ 、 らの各々を、
作らしめる❗
、
遺伝子 らの
日頃の仕事ら、の、
健全性 ✔️ にもよって
、
その、健全性ら、 を、
能 ヨ く、
成し付け得る
、 のに必要な
、
より、 あるべき、 代謝 ✔️
ら、が、
よく、 成し付けられ得てある、
場合らにおいては
、
ケガ 、でも、しない限りは
、
より、 万病を成さず ✔️
に、
人々は、 在り続ける、
が
、
その、 遺伝子 ✔️
ら、が、
老化を、成し、進めたり、
健全性を、 より、 失わされたり、
すると、
より、 万病のどれ彼や、
死を、 その人々に成す向きへ、
余計な、圧力が掛かり、
それらの健全な人々においては、
より、 全く、 軽く済んで、
完治する❗
、
ありふれた、
感染症 ✔️
、 などで、
その人々が、
より、 呆気なく、 死んだり、
ひどく、 重症化したりする、 向きへも、
余計な、 圧力が掛かる。
人々の、
遺伝子 ✔️ ら、や、
体の構造ら、とか、
あり得る、
機能ら、の、健全性ら、 を、
能く、
成し付ける、 のに必要な
、
より、 あるべき、 代謝 ✔️
ら、 を、
能く、 成し付ける
、 には
、
酵素 コウソ 、 としての、
タンパク質 ✔️
、 たちのどれ彼を、
必ず、
その➖方に、 含む
、
あるべき、 代謝員 ✔️
ら、 をの、
飲み食いなどによる、
摂取ら、
が、 必要であり、
その摂取らにおいて、
より、
漏れ、ら、を、成し付けない❗
事が、 必要だ、
が、
代謝 ✔️ らの各々においては
、
タンパク質 ✔️ な、
酵素 コウソ 、 と
、
補酵素 ホコウソ 、
な、
ビタミン ✔️
、らの、どれ彼か
、
補因子 、 な、 ミネラル ✔️
、らのどれ彼かと、
が、
➖定の度合い以上で、
合体 ✔️ する
、
事が、 必要とされてあり、
その度合いが、
➖定 以下である、
場合らにおいては
、
その 代謝 ✔️ 、らは、 成されず ✔️
、
万病 ✔️ への 要因性を、 それ自らに、
帯びる事になる。
他の、 大勢の人々にとっては、
全く、 問題性の無い🎵
、
特定の、 代謝員 ✔️ ら、 をの、摂取ら、の、
成しようら、 が
、
特定の人々には、
その、あるべき、 代謝 ✔️ ら、 での、
不⚡️ 足 ✔️ 性 ら、 を、 成すべくして、 成す
、
不 ✔️ ➕分なものである
事が、 あり得
、
そうした、 考えよう、は
、
ほぼ、 同➖な物らを飲み食いし
、
同じような、 訓練
ら、などでの、
運動性らを成し付けもし
、
同じような、 寮での、
暮らしようらも成し
、
遺伝子らの、
より、 似たり寄ったりな、
同➖な、人種の、 人々
、 などが、
万病の、 どれ彼らを成して、
重症化もし、 死んだりもする、
人々と
、
それらを成しても、
より、
軽く済まして、 完治し得たり、
あるいは、
全く、 それらを成さずに、
その健康性を成し続け得たりする、
人々とに、
分かれる
、
事 などへ宛てて
、
それを構成し得る、
因果 ✔️ 性 などを、
よく、辻褄の合う
形で、
説明し得る、 考えようら
、 への、
照らし合わせの基準系に、 成り得る、
もの、であり
、
現に、
三石分子栄養学 ➕ 藤川院長系 においては、
そう、され得てある。
この、 確率的な、 親和力
ら、 での、
不⚡️ 足 ✔️ 性
ら、 を、
より、
埋め余し得る❗
摂取らの成しようら、
を、
より、
成さなければ、 成さない ✔️ 程に
、
その手の人々は、
健康性や、
完治 ✔️ 、 、 自らを、
より、 遠ざける、 向きへ、
余計な、 圧力らを掛け増す事になる 】
。
🤽🪞🦈 〘 溺れ🌙 得よう、 への 気付き法🌙 ら🌙
https://blog.goo.ne.jp/callthefalcon01/e/b5a87b9651fd4652f3b252d04572741c
🦖🌊🌘 喉 で、 つながり得る⚡️ 、 餅ら ✔️
https://blog.goo.ne.jp/callthefalcon01/e/ce02a3b9abb229022e63a4bc882ed7f1
🦖🌖🏄️ みぞし法🎵 ; ハイムリック法🎵
https://blog.goo.ne.jp/callthefalcon01/e/6ae5ecb970fc0fb9264978f27a3e5388
🦖🌎🏄️ 『 分離🌙 』 性 による、 善悪🌙
https://blog.goo.ne.jp/callthefalcon01/e/8c6cb50f67274210c07446eb80877f52
🌍🌎 『 メチル基 CH3 ➕ B3 』
;
メチル基 CH3 、 の 不足 ✔️
は、
脂肪肝 ✔️ 、により、 生じる❗
;
藤川徳実院長❗
;
・ナイアシン は、
CH3 、を 、 自らの側へ受け容れる、
メチル基 、への、受容体 なので、
理論的には、
メチル基での不足が、起こり得る❗
。
・その場合においては
、
CH3 、を、 自らの側から、他者へ与え付け得る
、
メチル基、 をの、 供与体である
、
レシチン 1200 mg ✖️ 2
、
を併用すれば、
メチル基での不足は、容易に解消できる❗
。
・もしくは、
メチル基 をの供与体 な、 ベタイン 、を併用する。
ナイアシン・アミドで、不調になられる方は、
メチル基 が 不足しやすい ✔️
、
体質の可能性があります。
まず、
高 ✔️ タンパク / 低 ✔️ 糖質 食で、
脂肪肝 ✔️ を改善させる❗
。
そして、
ナイアシン アミド に、
レシチン 1200 mg ✖️ 2
、 を併用する。
当院の患者で、
” レシチン 7000 mg 程度を併用する❗
と、
ナイアシン 、による効果が高まる❗ ”
、
と言っていた人がいます 】
。
🌍🌎 武漢 コロナ ✔️ 、 などに 感染したら、
飲んでは、いけない ✔️ 、 薬ら ;
https://blog.goo.ne.jp/callthefalcon01/e/19dbcde1460060f8ffb5b682fed103e4
🌕🌍 『 レシチン 』
;
【 lecithin
、 は、
グリセロ・リン 脂質 の ➖種。
自然界の動植物において、
すべての細胞らの中に在り
、
生体膜 をの 主要な構成分。
レシチン
、 という名は、
ギリシャ語で、 卵黄🎵 を意味する 、
λέκιθος ( lekithos 、 レキトス )
に由来する。
レシチン 、は、
元は、
リン 脂質 の ➖種類である
、
ホスファチジル コリン
( Phosphatidyl choline ) 、への、
別名であったが
、
現在では
、
リン 脂質 を含む、 脂質 から成る、
製品のことを、 総称して、
レシチン
、 と呼んでいる。
市場 などでは、 原料に、
何を使用しているかで、分類され
、
卵黄 を 原料とするものは、
「 卵黄 レシチン 」
、
大豆を原料とするものは、
「 大豆 レシチン 」
、
と呼ばれ、区別される。
レシチン の 特性として
、
油を、 水に分散させて、
粒の各々を作る
、
『 乳化 力 ✔️ 』
、と
、
皮膚 や 粘膜 から、
物質を透過させて吸収する❗
、
浸透の作用がある。
これらがゆえに、
医薬用な、 リポソーム 、への材料、とか、
静脈への注射用な、 脂肪 乳剤 、に、
痔 や 皮膚病 への 治療薬として、
利用されている。
体内で、
脂肪 ✔️ 、が、
エネルギー として、
利用され、貯蔵される際に
、
タンパク質 、 と結びついて、
『 リポ・タンパク質 』 、 となり
、
血潮らの中を移動する
が、
この、 タンパク質 、と、 脂肪 との結合に、
『 レシチン 』 、を必要とする❗
。
体内の、 レシチン の 総量は、
体重が、 60 Kg
、 の、 ヒトで、
6百 グラム 、程度である。
レシチン の 不⚡ 足
は、
疲労 ✔️ 、 免疫力の低下 ✔️ 、 不眠 ✔️ 、
動脈 硬化 ✔️ 、 糖尿病 ✔️ 、
悪玉 コレステロール の 沈着 ✔️
、
などの、
多くの症状ら、 への、 原因ら、の、
➖定の度合いで、 あり得る 】 ;
。
🦈⛲ 肺 、が、 鼻水のごとき液で、覆われ、固められて、
窒息⚡️ 死 ✔️
https://blog.goo.ne.jp/callthefalcon01/e/fa6f1d716e3be15cd662c640c2b4bda3
🌬️🦅🌊 人々の体で 使い回される、元素 🌙 ら
https://blog.goo.ne.jp/callthefalcon01/e/c917537fcc40713eadcb3c19d859ac45
🌬️🌃🌊 扌工 知惟 テクシー : AI 、 による 概要 🌙
数学では、 0 の 階乗は、 1 と決まっており、
式で表すと
「 0❗️ = 1 」 となります。
また、 10 などの 0 乗 も、 1 です。
0 乗 が、 1 であることを説明する例として、
コピー用紙を折る 問題が挙げられます。
コピー用紙を 1 枚 を 手にして、 何回 を 折れるかに挑戦してみましょう。
そうしたら、 1 回も 折らない 🌙
最初の状態が、 0 回 を 折ることであることを実感してみます。
なるほど、 0 回 を 折ること、 すなわち
0 乗 は、 元からの 厚さ : 存在 の 度合い 、 が
同じ、 すなわち
1 倍 である、 と、 実感できるはずです。
🌬️🚰🌊 空間 情報 クラブ
| インフォマティクス 運営の Web メディア
なぜ、 0 乗 は、 1 なのか❔
2024年1月5日
2³ ( 2 の 3 乗 ) は
2 ✖️ 2 ✖️ 2 のことで、 8 である ことが
分かりやすいのに対して、
2⁰ が、 1 であることは、 イマイチにて
ピンときません。
計算についての説明の前に、 何乗の計算にまつわる
用語の説明をしておきます。
冪 ・冪乗 ・累乗 ・指数 ・底
四則演算である、
たし算 ( 加法 ) 、 ひき算 ( 減法 )、 かけ算 ( 乗法 ) 、
割り算 ( 除法 ) の 計算の結果が、
それぞれにて、 和 、 差 、 積 、 商 です。
ab の 計算結果を、 冪 ( べき ) 、
ab の 演算 を 、 冪乗 、 または
べき乗 、 と呼びます。
冪 ( べき ) とは、 おおい隠す ことです。
冪 = 冖 ( べき ) ➕ 幕 ですが、
「 冖 」 は、 布で 物を覆うこと、
「 幕 」 で おおい隠す
ことを示しています。
略字として、 「 巾 」 と書くこともあります。
累 とは、 かさねることです。
累乗 は、 「 かさねた乗算 」 の意味です。
わが国の教科書では、 累乗 が使われています。
冪 は、 常用漢字・当用漢字には 含まれていません。
そこで、 代わりに使われることになったのが
平仮名の 「 べき 」 と、 「 累 」 です。
もとからの、 冪 と、 後から使われることになる、 累 ですが、
使い方に 違いがあります。
指数 が、 自然数の場合の 冪乗 を
累乗 と区別する 使い方もありますが、
冪乗 ・べき乗 ・累乗 は
ほとんど 同じ 意味 で 使われます。
演算の結果は、 冪 であり、 累 では ありません。
また、 冪級数 ・巾級数 という、 数学用語はありますが、
累級数 とは、 いいません。
🌬️🏜️🌊 Wikipedia 階乗 🌙
数学において、 自然数 n の 階乗
( かいじょう、 英: factorial )
n ❗️ とは、 1 から n までの
全ての 整数の積 🌙 のことである。
例えば、
6❗️ = 6 ✖️ 5 ✖️ 4 ✖️ 3 ✖️ 2 ✖️ 1
= 720
空積の規約の下で、 0❗️ = 1
と定義する。
階乗は、 数学の様々な場面に出現するが、 特に
組合せ論 、 代数学 、 解析学 などが 著しい。
階乗 の 最も基本的な出自は
n 個 の 相異なる対象を 1 列 に並べる 方法
( 対象の置換 オッケ ) の 総数が
n❗️ 通り である
という、 事実である。
🌬️🏇🌊 YouTuber :
奇数 の 2 乗 から、 1 を引いた数は
8 の 倍数になるって 、 マジ❔
9の2乗 ➖ 1 = 80
7の2乗 ➖ 1 = 48
3の2乗 ➖ 1 = 8
5の2乗 ➖ 1 = 24
🌬️🚵🌊 Wikipedia 🌙
🌬️🏄️🌊 帰納 🌙
個別的・特殊的な 事例から
➖般的・普遍的な 規則・法則を見出そうとする
論理的推論の方法
この項目では、
Induction をの訳としての 「 帰納 」 、 特に
枚挙的 帰納法 について 説明しています。
Recursion をの訳としての 「 帰納 」 については
「 再帰 」 をご覧ください。
帰納 ( きのう、 英: Induction、 希: επαγωγή
( エパゴーゲー ) とは、
個別的・特殊的な 事例から、 ➖般的・普遍的な
規則・法則 を見出そうとする 論理的推論の方法のこと。
演繹においては
前提が、 真であれば、 結論も、 必然的に真であるが、
帰納においては
前提が、 真であるからといって
結論が 真である ことは、 保証されない。
なお、 数学的帰納法 ・構造的帰納法 ・整礎帰納法 ・完全帰納法
・累積帰納法 ( 英語版 ) ・超限帰納法 などの 帰納法は、
その名前と違い、 帰納ではなく、 演繹 である。
🌬️🦣🌊 AI による 概要 🌙
演繹 ( えんえき ) とは、
大きな前提から、 結論を推論する思考法で、
論理学の考え方の➖つです。
演繹法 とも呼ばれ、 演繹的 推理 とも呼ばれます。
演繹法では、 ➖般論や 社会通念上のルール、 規則 などの
大前提を基本に、 さらに、 前提を加えて
条件を付けながら、 論理を積み重ねて、 結論を導き出します。
たとえば、
「 A = B 」 と 「 B = C 」 が成り立つ場合
「 A = C 」 であると考えます。
演繹法の特徴は、
➖般の人が納得できる前提を 基本に
論理を展開する ため、
誰でも 納得しやすく、 複雑な 提是 テゼ : テーマ 、でも
論理的な 結論を出せる ことです。
また、 理論的で、 説得力のある 説明ができます。
🌬️🌪️🌊 東大塾長 の 山田 🌙
実際は、 演繹法 である
【 数学的 帰納法 】
証明法を 例題で わかりやすく ( 不等式 など )
東大塾長の山田です。
この 辺辞 ペジ では、 数学 B の
「 数学的 帰納法 」 について解説します。
今回は、 数学的帰納法の考え方・解き方を, 大学受験で頻出の問題
( 等式 ・倍数 ・不等式 ・漸化式 ) を通して
具体的に、 超わかりやすく解説していきます。
1. 数学的帰納法とは❔ 超わかりやすく説明
漸化式では
[1] a1 = 1
[2] an ➕ 1 = an ➕ n
( n = 1, 2, 3, ⋯ )
[1] を もとにして, [2] において
n = 1, 2, 3, ⋯ とすると
a2 = a1 ➕ 1 = 1 ➕ 1 = 2
a3 = a2 ➕ 2 = 2 ➕ 2 = 4
a4 = a3 ➕ 3 = 4 ➕ 3 = 7
⋯⋯⋯
となり,
a1, a2, ⋯, an, ⋯ の値が、 1 通りに 定まります。
つまり,
「 初項 a1 」 と
「 ak から ak ➕ 1 を求める 規則 」 が与えられれば,
すべての自然数 n について,
an を定めることができます。
これと同じような考え方で,
自然数 n に関する 命題 P が
すべての自然数 n について成り立つ ことを証明したいときに
[1] n = 1 のとき 、 P が成り立つ。
[2] n = k のとき 、 P が成り立つ、 と仮定すると,
n = k ➕ 1 のときにも、 P が成り立つ。
この [1], [2] を示す ことによって
[1] から n = 1 のとき、 P は 成り立つ。
① と [2] から
n = 1 ➕ 1 = 2 のときも
P は 成り立つ。
さらに, ② と [2] から
n = 2 ➕ 1 = 3 のときも
P は 成り立つ。
同様に 、 n = 4, 5, 6, ⋯ のときにも
P は 成り立ち, 結局は、
すべての自然数 n について 、 P は、 成り立つ。
ことがいえます。
このような証明法を 数学的 帰納法 といいます。
2. 数学的帰納法 の 等式の証明問題 🌙
例題 1
n が 自然数のとき, 数学的帰納法を用いて、 次の等式を証明せよ。
12 ➕ 22 ➕ 32 ➕ ⋯ ➕ n2
= 16 n ( n ➕ 1 ) ( 2n ➕ 1 ) ⋯①
【 証明 】
[1] n = 1 のとき
( 左辺 ) = 11 = 1
( 右辺 ) = 16 ⋅ 1 ⋅ ( 1 ➕ 1 ) ( 2 ⋅ 1 ➕ 1 )
= 1
よって, n = 1 のとき、 ① は 成り立つ。
[2] n = k のとき,
① が 成り立つ と仮定すると
12 ➕ 22 ➕ 32 ➕ ⋯ ➕ k2
= 16 k ( k ➕ 1 ) ( 2k ➕ 1 ) ⋯②
n = k ➕ 1 のときを考えると, ② から
12 ➕ 22 ➕ 32 ➕ ⋯ ➕ k2 ➕ ( k ➕ 1 )2
= 16 k ( k ➕ 1 ) ( 2k ➕ 1 ) ➕ ( k ➕ 1 )2
= 16 ( k ➕ 1 )
{ k ( 2k ➕ 1 ) ➕ 6 ( k ➕ 1 ) }
= 16 ( k ➕ 1 ) ( 2k2 ➕ 7k ➕ 6 )
= 16 ( k ➕ 1 ) ( k ➕ 2 ) ( 2k ➕ 3 )
= 16 ( k ➕ 1 )
{ ( k ➕ 1 ) ➕ 1 }
{ 2 ( k ➕ 1 ) ➕ 1 }
よって,
n = k ➕ 1 のときにも、 ① は 成り立つ。
[1],[2] から, すべての自然数 n について
① は 成り立つ。
椪堵 ポント : Point 🌙
[1] n = 1 のときを証明する。
[2] n = k のときを仮定し,
n = k ➕ 1 のときを証明する。
[2] の証明では,
n = k のとき 成り立つ と仮定した 式を使って,
n = k ➕ 1 のときの 式変形をしていくのが、 定石です。
また, 上の解答の赤字の部分は,
数学的帰納法の決まり文句です。
答案は、 この通りに つくっていけば、 OK です❗️
🌬️🏎️🌊 GIGAZINE 🌖🌙
2018年 1月16日 19時00分 叉兌 サエツ : サイエンス 🌙
キリスト教暦での、 第 千5百年代 な、 16世紀に
メキシコの アステカ文明を壊滅的な状況に追い込んだ伝染病の実態が
「 死者の歯 」 から浮き彫りに
By Siddie Nam
日本では、 戦国時代の真っ盛りであった、 1519 年 に
スペイン人の エルナン・コルテス が、 メキシコに上陸してから
数➕年の間に、 先住民族である アステカ人の間では
人類史上にて 最悪 とも言われる、 謎の伝染病がまん延して
壊滅的な状況に陥りました。
埋葬されていた 当時の死者の歯を調査したところ、 その原因は
「 サルモネラ菌 」 の ➖種であった
可能性が浮かび上がっています。
Salmonella enterica genomes from v ictims
of a major sixteenth-century epidemic in Mexico
|
Nature Ecology & Evolution
https://www.nature.com/articles/s41559-017-0446-6
A New Clue to the 1545 Cocolitzli Epidemic in Mexico -
The Atlantic
https://www.theatlantic.com/science/archive/2018/01/salmonella-cocoliztli-mexico/550310/
16世紀の メキシコ の 壊滅的な伝染病は
サルモネラ菌 が 原因 、 と考えられる
|
Nature Ecology and Evolution
|
Nature Research
http://www.natureasia.com/ja-jp/research/highlight/12328
この研究を進めたのは、
マックス・プランク・ヒト・サイエンス研究所の人類学者である
キルステン・ボス氏らによる研究 致廡 チム : チーム 。
伝染病で亡くなった住人の 歯の内部に含まれる
参封 サンプ➖ : サンプル 、 を分析することで
病原体の DNA を抽出し、
アステカ人を破滅寸前に追いやった原因を明らかにしています。
16世紀に メキシコに上陸した スペイン人は、
天然痘や 麻疹、 チフス ⚡️ などの
多くの病気を現地に持ち込んだ、 といわれており、
現地の人々は、 これらを総称して、 「 ココリツトリ 」
と呼んでいた、 とのこと。
1545年に、 最初の流行が発生し、 その後な、 1576 年に、 再び
被害が拡大します。
そのたびに、 数百万人単位の死者が続出し、
アステカ文明の人口は、 2000万人から 200万人へと激減した
とみられており、
その様子を目の当たりにした、 フランシスコ会修道士は
「 朝から夕方にかけて、 司祭たちは、 死体を運び、
それを溝に放り込んで埋めた 」 、 と記しています。
この ココリツトリ の詳細は、 これまでに、
ほとんどが、 明らかにされておらず、
天然痘 や 麻疹 などの 病気である、 と考えられてきましたが、
最新の DNA 分析 技術 を用いることで
その正確な姿が明らかにされてきています。
研究を行った ボス氏は、 メキシコの南部にある
大規模な ミシュテカ の 墓地に埋葬された 死者
11 人の歯 を取り出して、 その中に残された病原体の
DNA を詳細に調査しました。
🐉🌍🏝️ 『 RNA 疫鎮 問題⚡️ 』
:
【 遺伝子 : DNA : デオキシ リボ 核酸 、
らは、
毎日に、 いつでも、 色々な アミノ酸 たち から、
色々な タンパク質 らの 各々 を 作り出さしめる
仕事 ら を させられており
、
そのお蔭で、 我々なる 人 などの、
命 と 健康性 とが、 成し付けられ得て来てあり
、
準 遺伝子 とも 言うべき、
RNA : リボ 核酸 、 たちの内の
、
伝令 RNA : メッセンジャー RNA :
m RNA 、 たちの各々は
、
遺伝子 を 構成する
3つ で ➖つ の 並びよう な 塩基 らの
その 顔触れ に 対応せる
塩基 らを 自らの側に 揃 ソロ え
、
運搬 RNA : トランスファー RNA :
t RNA 、 をして
、
リボゾーム へ 持って行かせ
そこで、 その 塩基 ら の ➖つ ごと の 並びよう へ 対応する
➖種員 の アミノ酸 を 特定する
という事を繰り返して
色々な アミノ酸 たち から、 立体的に
特定の タンパク質 を 作り出さしめており
、
それらを 日常的に 成し行い付け得てある
のに対して
、
RNA ワクチン らは
、
その体の主の 遺伝性 らとは、
関係 が 無く⚡️
その主へ至る 累代員らの 可能的な 遺伝性 らへの
淘汰圧ら の 影響性 らに、
より、 関わり が 無い⚡️
が ゆえもあって
、
その体ごとの、 遺伝子らの、
より、 全体な 働き得ようらへ、
どんな 阻害性 の 影響性 らや
どんなに 余計な 過剰性 の 影響性 ら などを
与え付け得るか、 といった 向きの
可害 ベガイ : リスク 、 ら など を、
その宛ての 主らへ、 宛て付けるものでもある
ので
、
出来る得る限り、
我彼への その投与を避けて、
より、 質的な 栄養 らをの 充足 と
適度な 運動性 らとに よる
事の方が、
人々が、 その命と健康性とを成し付けるのに必要な
代謝 らを、
より、 漏れ⚡️ を 無しに、
成し付け得てゆくようにする上で、
より、 望ましい もの として、 ある☀ 】
歯の中の、 柔らかく生きている組織である 歯髄には
多くの血管が通っており、
血液の中に入り込んだ 病原体も、
もれなく、 歯髄の中に流れ込みます。
そして、 患者の死後には、
歯の外側にある、 硬い エナメル質 が
何世紀もの間にわたって、 病原体の DNA を保護する
役目を担う、 とのこと。
ボス氏は、 この血液の痕跡から、 DNA を抽出する
新しい技術を用いることで、 その病原体が
病原菌の➖種である、 サルモネラ菌の
DNA を 構成する、
塩基 配列 を持つ ことを発見しました。
By John Patrick Robichaud
この病原菌は、
「 チフス を引き起こす 細菌 」 を意味する
Salmonella enterica あるいは
S. enterica と呼ばれており、
今回に、 この菌が見つかったことで、
アステカ文明を破滅に追いやる原因の一つとなった伝染病は
チフス であったことを強く裏付けています。
さらに、 スペイン人が上陸する以前に死亡していた
5 人の 歯髄 参封 サンプ➖ には
S. enterica が 含まれていない ことも、
この説を裏付けるものとなっている、 とのこと。
チフス による 発熱は、
病気の人の糞便で汚染された ⚡️ 食物や水を介して広がるもので、
現代の社会では、 多くの人が密集している
貧しい環境で、 多くみられます。
論文では、 サルモネラ菌 が
他の病原体と相互作用した可能性がある
ことも 認めており、
今回に用いられた手法も、 その可能性を残すものである
とのこと。
この手法では、 DNA を検出することしかできない中で、
➖部の ウイルス は、
RNA で 分裂を行っている ことから、
今回の手法では、 見つけられなかった
他の要因があることを 研究 致廡 チム は、 認めています。
しかしながら、
古い DNA を用いた分析手法は、
これまで知ることができなかった
過去の状況を知る 手がかりになる ことが期待されています。
フランスの公立大学・エクス=マルセイユ大学の微生物学者、
ニコラス・ラスコヴァン氏は
「 この、 古い DNA に関する分野で、
新たな 捨歩 ステプ : ステップ は、
人間 への 共生物である 細菌 に
注目を集めることにつながるでしょう 」
と語っています。
;
解放🎵 を急ぐべき、 シナ⚡ による、
桜木 琢磨 市議 らをの 実質 での 拉致⚡ たる 事件ら⚡
;
🦋⛲ 日本医学 ; 和法🎵
三石分子栄養学 ➕ 藤川徳美院長系 ; 代謝医学❗
;
人々の体らの各々の、
構造らや、 機能ら
、 が、
その遺伝子らも含まれてある、
細胞ごとにおいて、
色々な アミノ酸 たちから
特定の、
タンパク質 ✔️ 、 らの各々を、
作らしめる❗
、
遺伝子 らの
日頃の仕事ら、の、
健全性 ✔️ にもよって
、
その、健全性ら、 を、
能 ヨ く、
成し付け得る
、 のに必要な
、
より、 あるべき、 代謝 ✔️
ら、が、
よく、 成し付けられ得てある、
場合らにおいては
、
ケガ 、でも、しない限りは
、
より、 万病を成さず ✔️
に、
人々は、 在り続ける、
が
、
その、 遺伝子 ✔️
ら、が、
老化を、成し、進めたり、
健全性を、 より、 失わされたり、
すると、
より、 万病のどれ彼や、
死を、 その人々に成す向きへ、
余計な、圧力が掛かり、
それらの健全な人々においては、
より、 全く、 軽く済んで、
完治する❗
、
ありふれた、
感染症 ✔️
、 などで、
その人々が、
より、 呆気なく、 死んだり、
ひどく、 重症化したりする、 向きへも、
余計な、 圧力が掛かる。
人々の、
遺伝子 ✔️ ら、や、
体の構造ら、とか、
あり得る、
機能ら、の、健全性ら、 を、
能く、
成し付ける、 のに必要な
、
より、 あるべき、 代謝 ✔️
ら、 を、
能く、 成し付ける
、 には
、
酵素 コウソ 、 としての、
タンパク質 ✔️
、 たちのどれ彼を、
必ず、
その➖方に、 含む
、
あるべき、 代謝員 ✔️
ら、 をの、
飲み食いなどによる、
摂取ら、
が、 必要であり、
その摂取らにおいて、
より、
漏れ、ら、を、成し付けない❗
事が、 必要だ、
が、
代謝 ✔️ らの各々においては
、
タンパク質 ✔️ な、
酵素 コウソ 、 と
、
補酵素 ホコウソ 、
な、
ビタミン ✔️
、らの、どれ彼か
、
補因子 、 な、 ミネラル ✔️
、らのどれ彼かと、
が、
➖定の度合い以上で、
合体 ✔️ する
、
事が、 必要とされてあり、
その度合いが、
➖定 以下である、
場合らにおいては
、
その 代謝 ✔️ 、らは、 成されず ✔️
、
万病 ✔️ への 要因性を、 それ自らに、
帯びる事になる。
他の、 大勢の人々にとっては、
全く、 問題性の無い🎵
、
特定の、 代謝員 ✔️ ら、 をの、摂取ら、の、
成しようら、 が
、
特定の人々には、
その、あるべき、 代謝 ✔️ ら、 での、
不⚡️ 足 ✔️ 性 ら、 を、 成すべくして、 成す
、
不 ✔️ ➕分なものである
事が、 あり得
、
そうした、 考えよう、は
、
ほぼ、 同➖な物らを飲み食いし
、
同じような、 訓練
ら、などでの、
運動性らを成し付けもし
、
同じような、 寮での、
暮らしようらも成し
、
遺伝子らの、
より、 似たり寄ったりな、
同➖な、人種の、 人々
、 などが、
万病の、 どれ彼らを成して、
重症化もし、 死んだりもする、
人々と
、
それらを成しても、
より、
軽く済まして、 完治し得たり、
あるいは、
全く、 それらを成さずに、
その健康性を成し続け得たりする、
人々とに、
分かれる
、
事 などへ宛てて
、
それを構成し得る、
因果 ✔️ 性 などを、
よく、辻褄の合う
形で、
説明し得る、 考えようら
、 への、
照らし合わせの基準系に、 成り得る、
もの、であり
、
現に、
三石分子栄養学 ➕ 藤川院長系 においては、
そう、され得てある。
この、 確率的な、 親和力
ら、 での、
不⚡️ 足 ✔️ 性
ら、 を、
より、
埋め余し得る❗
摂取らの成しようら、
を、
より、
成さなければ、 成さない ✔️ 程に
、
その手の人々は、
健康性や、
完治 ✔️ 、 、 自らを、
より、 遠ざける、 向きへ、
余計な、 圧力らを掛け増す事になる 】
。
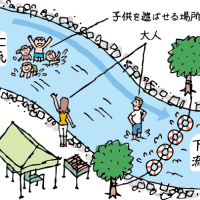
🤽🪞🦈 〘 溺れ🌙 得よう、 への 気付き法🌙 ら🌙
https://blog.goo.ne.jp/callthefalcon01/e/b5a87b9651fd4652f3b252d04572741c
🦖🌊🌘 喉 で、 つながり得る⚡️ 、 餅ら ✔️
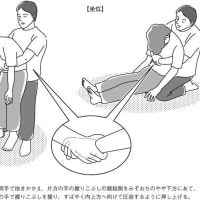
https://blog.goo.ne.jp/callthefalcon01/e/ce02a3b9abb229022e63a4bc882ed7f1
🦖🌖🏄️ みぞし法🎵 ; ハイムリック法🎵
https://blog.goo.ne.jp/callthefalcon01/e/6ae5ecb970fc0fb9264978f27a3e5388
🦖🌎🏄️ 『 分離🌙 』 性 による、 善悪🌙
https://blog.goo.ne.jp/callthefalcon01/e/8c6cb50f67274210c07446eb80877f52
🌍🌎 『 メチル基 CH3 ➕ B3 』
;
メチル基 CH3 、 の 不足 ✔️
は、
脂肪肝 ✔️ 、により、 生じる❗
;
藤川徳実院長❗
;
・ナイアシン は、
CH3 、を 、 自らの側へ受け容れる、
メチル基 、への、受容体 なので、
理論的には、
メチル基での不足が、起こり得る❗
。
・その場合においては
、
CH3 、を、 自らの側から、他者へ与え付け得る
、
メチル基、 をの、 供与体である
、
レシチン 1200 mg ✖️ 2
、
を併用すれば、
メチル基での不足は、容易に解消できる❗
。
・もしくは、
メチル基 をの供与体 な、 ベタイン 、を併用する。
ナイアシン・アミドで、不調になられる方は、
メチル基 が 不足しやすい ✔️
、
体質の可能性があります。
まず、
高 ✔️ タンパク / 低 ✔️ 糖質 食で、
脂肪肝 ✔️ を改善させる❗
。
そして、
ナイアシン アミド に、
レシチン 1200 mg ✖️ 2
、 を併用する。
当院の患者で、
” レシチン 7000 mg 程度を併用する❗
と、
ナイアシン 、による効果が高まる❗ ”
、
と言っていた人がいます 】
。
🌍🌎 武漢 コロナ ✔️ 、 などに 感染したら、
飲んでは、いけない ✔️ 、 薬ら ;
https://blog.goo.ne.jp/callthefalcon01/e/19dbcde1460060f8ffb5b682fed103e4
🌕🌍 『 レシチン 』
;
【 lecithin
、 は、
グリセロ・リン 脂質 の ➖種。
自然界の動植物において、
すべての細胞らの中に在り
、
生体膜 をの 主要な構成分。
レシチン
、 という名は、
ギリシャ語で、 卵黄🎵 を意味する 、
λέκιθος ( lekithos 、 レキトス )
に由来する。
レシチン 、は、
元は、
リン 脂質 の ➖種類である
、
ホスファチジル コリン
( Phosphatidyl choline ) 、への、
別名であったが
、
現在では
、
リン 脂質 を含む、 脂質 から成る、
製品のことを、 総称して、
レシチン
、 と呼んでいる。
市場 などでは、 原料に、
何を使用しているかで、分類され
、
卵黄 を 原料とするものは、
「 卵黄 レシチン 」
、
大豆を原料とするものは、
「 大豆 レシチン 」
、
と呼ばれ、区別される。
レシチン の 特性として
、
油を、 水に分散させて、
粒の各々を作る
、
『 乳化 力 ✔️ 』
、と
、
皮膚 や 粘膜 から、
物質を透過させて吸収する❗
、
浸透の作用がある。
これらがゆえに、
医薬用な、 リポソーム 、への材料、とか、
静脈への注射用な、 脂肪 乳剤 、に、
痔 や 皮膚病 への 治療薬として、
利用されている。
体内で、
脂肪 ✔️ 、が、
エネルギー として、
利用され、貯蔵される際に
、
タンパク質 、 と結びついて、
『 リポ・タンパク質 』 、 となり
、
血潮らの中を移動する
が、
この、 タンパク質 、と、 脂肪 との結合に、
『 レシチン 』 、を必要とする❗
。
体内の、 レシチン の 総量は、
体重が、 60 Kg
、 の、 ヒトで、
6百 グラム 、程度である。
レシチン の 不⚡ 足
は、
疲労 ✔️ 、 免疫力の低下 ✔️ 、 不眠 ✔️ 、
動脈 硬化 ✔️ 、 糖尿病 ✔️ 、
悪玉 コレステロール の 沈着 ✔️
、
などの、
多くの症状ら、 への、 原因ら、の、
➖定の度合いで、 あり得る 】 ;
。
🦈⛲ 肺 、が、 鼻水のごとき液で、覆われ、固められて、
窒息⚡️ 死 ✔️
https://blog.goo.ne.jp/callthefalcon01/e/fa6f1d716e3be15cd662c640c2b4bda3
🌬️🦅🌊 人々の体で 使い回される、元素 🌙 ら
https://blog.goo.ne.jp/callthefalcon01/e/c917537fcc40713eadcb3c19d859ac45
🌬️🌃🌊 扌工 知惟 テクシー : AI 、 による 概要 🌙
数学では、 0 の 階乗は、 1 と決まっており、
式で表すと
「 0❗️ = 1 」 となります。
また、 10 などの 0 乗 も、 1 です。
0 乗 が、 1 であることを説明する例として、
コピー用紙を折る 問題が挙げられます。
コピー用紙を 1 枚 を 手にして、 何回 を 折れるかに挑戦してみましょう。
そうしたら、 1 回も 折らない 🌙
最初の状態が、 0 回 を 折ることであることを実感してみます。
なるほど、 0 回 を 折ること、 すなわち
0 乗 は、 元からの 厚さ : 存在 の 度合い 、 が
同じ、 すなわち
1 倍 である、 と、 実感できるはずです。
🌬️🚰🌊 空間 情報 クラブ
| インフォマティクス 運営の Web メディア
なぜ、 0 乗 は、 1 なのか❔
2024年1月5日
2³ ( 2 の 3 乗 ) は
2 ✖️ 2 ✖️ 2 のことで、 8 である ことが
分かりやすいのに対して、
2⁰ が、 1 であることは、 イマイチにて
ピンときません。
計算についての説明の前に、 何乗の計算にまつわる
用語の説明をしておきます。
冪 ・冪乗 ・累乗 ・指数 ・底
四則演算である、
たし算 ( 加法 ) 、 ひき算 ( 減法 )、 かけ算 ( 乗法 ) 、
割り算 ( 除法 ) の 計算の結果が、
それぞれにて、 和 、 差 、 積 、 商 です。
ab の 計算結果を、 冪 ( べき ) 、
ab の 演算 を 、 冪乗 、 または
べき乗 、 と呼びます。
冪 ( べき ) とは、 おおい隠す ことです。
冪 = 冖 ( べき ) ➕ 幕 ですが、
「 冖 」 は、 布で 物を覆うこと、
「 幕 」 で おおい隠す
ことを示しています。
略字として、 「 巾 」 と書くこともあります。
累 とは、 かさねることです。
累乗 は、 「 かさねた乗算 」 の意味です。
わが国の教科書では、 累乗 が使われています。
冪 は、 常用漢字・当用漢字には 含まれていません。
そこで、 代わりに使われることになったのが
平仮名の 「 べき 」 と、 「 累 」 です。
もとからの、 冪 と、 後から使われることになる、 累 ですが、
使い方に 違いがあります。
指数 が、 自然数の場合の 冪乗 を
累乗 と区別する 使い方もありますが、
冪乗 ・べき乗 ・累乗 は
ほとんど 同じ 意味 で 使われます。
演算の結果は、 冪 であり、 累 では ありません。
また、 冪級数 ・巾級数 という、 数学用語はありますが、
累級数 とは、 いいません。
🌬️🏜️🌊 Wikipedia 階乗 🌙
数学において、 自然数 n の 階乗
( かいじょう、 英: factorial )
n ❗️ とは、 1 から n までの
全ての 整数の積 🌙 のことである。
例えば、
6❗️ = 6 ✖️ 5 ✖️ 4 ✖️ 3 ✖️ 2 ✖️ 1
= 720
空積の規約の下で、 0❗️ = 1
と定義する。
階乗は、 数学の様々な場面に出現するが、 特に
組合せ論 、 代数学 、 解析学 などが 著しい。
階乗 の 最も基本的な出自は
n 個 の 相異なる対象を 1 列 に並べる 方法
( 対象の置換 オッケ ) の 総数が
n❗️ 通り である
という、 事実である。
🌬️🏇🌊 YouTuber :
奇数 の 2 乗 から、 1 を引いた数は
8 の 倍数になるって 、 マジ❔
9の2乗 ➖ 1 = 80
7の2乗 ➖ 1 = 48
3の2乗 ➖ 1 = 8
5の2乗 ➖ 1 = 24
🌬️🚵🌊 Wikipedia 🌙
🌬️🏄️🌊 帰納 🌙
個別的・特殊的な 事例から
➖般的・普遍的な 規則・法則を見出そうとする
論理的推論の方法
この項目では、
Induction をの訳としての 「 帰納 」 、 特に
枚挙的 帰納法 について 説明しています。
Recursion をの訳としての 「 帰納 」 については
「 再帰 」 をご覧ください。
帰納 ( きのう、 英: Induction、 希: επαγωγή
( エパゴーゲー ) とは、
個別的・特殊的な 事例から、 ➖般的・普遍的な
規則・法則 を見出そうとする 論理的推論の方法のこと。
演繹においては
前提が、 真であれば、 結論も、 必然的に真であるが、
帰納においては
前提が、 真であるからといって
結論が 真である ことは、 保証されない。
なお、 数学的帰納法 ・構造的帰納法 ・整礎帰納法 ・完全帰納法
・累積帰納法 ( 英語版 ) ・超限帰納法 などの 帰納法は、
その名前と違い、 帰納ではなく、 演繹 である。
🌬️🦣🌊 AI による 概要 🌙
演繹 ( えんえき ) とは、
大きな前提から、 結論を推論する思考法で、
論理学の考え方の➖つです。
演繹法 とも呼ばれ、 演繹的 推理 とも呼ばれます。
演繹法では、 ➖般論や 社会通念上のルール、 規則 などの
大前提を基本に、 さらに、 前提を加えて
条件を付けながら、 論理を積み重ねて、 結論を導き出します。
たとえば、
「 A = B 」 と 「 B = C 」 が成り立つ場合
「 A = C 」 であると考えます。
演繹法の特徴は、
➖般の人が納得できる前提を 基本に
論理を展開する ため、
誰でも 納得しやすく、 複雑な 提是 テゼ : テーマ 、でも
論理的な 結論を出せる ことです。
また、 理論的で、 説得力のある 説明ができます。
🌬️🌪️🌊 東大塾長 の 山田 🌙
実際は、 演繹法 である
【 数学的 帰納法 】
証明法を 例題で わかりやすく ( 不等式 など )
東大塾長の山田です。
この 辺辞 ペジ では、 数学 B の
「 数学的 帰納法 」 について解説します。
今回は、 数学的帰納法の考え方・解き方を, 大学受験で頻出の問題
( 等式 ・倍数 ・不等式 ・漸化式 ) を通して
具体的に、 超わかりやすく解説していきます。
1. 数学的帰納法とは❔ 超わかりやすく説明
漸化式では
[1] a1 = 1
[2] an ➕ 1 = an ➕ n
( n = 1, 2, 3, ⋯ )
[1] を もとにして, [2] において
n = 1, 2, 3, ⋯ とすると
a2 = a1 ➕ 1 = 1 ➕ 1 = 2
a3 = a2 ➕ 2 = 2 ➕ 2 = 4
a4 = a3 ➕ 3 = 4 ➕ 3 = 7
⋯⋯⋯
となり,
a1, a2, ⋯, an, ⋯ の値が、 1 通りに 定まります。
つまり,
「 初項 a1 」 と
「 ak から ak ➕ 1 を求める 規則 」 が与えられれば,
すべての自然数 n について,
an を定めることができます。
これと同じような考え方で,
自然数 n に関する 命題 P が
すべての自然数 n について成り立つ ことを証明したいときに
[1] n = 1 のとき 、 P が成り立つ。
[2] n = k のとき 、 P が成り立つ、 と仮定すると,
n = k ➕ 1 のときにも、 P が成り立つ。
この [1], [2] を示す ことによって
[1] から n = 1 のとき、 P は 成り立つ。
① と [2] から
n = 1 ➕ 1 = 2 のときも
P は 成り立つ。
さらに, ② と [2] から
n = 2 ➕ 1 = 3 のときも
P は 成り立つ。
同様に 、 n = 4, 5, 6, ⋯ のときにも
P は 成り立ち, 結局は、
すべての自然数 n について 、 P は、 成り立つ。
ことがいえます。
このような証明法を 数学的 帰納法 といいます。
2. 数学的帰納法 の 等式の証明問題 🌙
例題 1
n が 自然数のとき, 数学的帰納法を用いて、 次の等式を証明せよ。
12 ➕ 22 ➕ 32 ➕ ⋯ ➕ n2
= 16 n ( n ➕ 1 ) ( 2n ➕ 1 ) ⋯①
【 証明 】
[1] n = 1 のとき
( 左辺 ) = 11 = 1
( 右辺 ) = 16 ⋅ 1 ⋅ ( 1 ➕ 1 ) ( 2 ⋅ 1 ➕ 1 )
= 1
よって, n = 1 のとき、 ① は 成り立つ。
[2] n = k のとき,
① が 成り立つ と仮定すると
12 ➕ 22 ➕ 32 ➕ ⋯ ➕ k2
= 16 k ( k ➕ 1 ) ( 2k ➕ 1 ) ⋯②
n = k ➕ 1 のときを考えると, ② から
12 ➕ 22 ➕ 32 ➕ ⋯ ➕ k2 ➕ ( k ➕ 1 )2
= 16 k ( k ➕ 1 ) ( 2k ➕ 1 ) ➕ ( k ➕ 1 )2
= 16 ( k ➕ 1 )
{ k ( 2k ➕ 1 ) ➕ 6 ( k ➕ 1 ) }
= 16 ( k ➕ 1 ) ( 2k2 ➕ 7k ➕ 6 )
= 16 ( k ➕ 1 ) ( k ➕ 2 ) ( 2k ➕ 3 )
= 16 ( k ➕ 1 )
{ ( k ➕ 1 ) ➕ 1 }
{ 2 ( k ➕ 1 ) ➕ 1 }
よって,
n = k ➕ 1 のときにも、 ① は 成り立つ。
[1],[2] から, すべての自然数 n について
① は 成り立つ。
椪堵 ポント : Point 🌙
[1] n = 1 のときを証明する。
[2] n = k のときを仮定し,
n = k ➕ 1 のときを証明する。
[2] の証明では,
n = k のとき 成り立つ と仮定した 式を使って,
n = k ➕ 1 のときの 式変形をしていくのが、 定石です。
また, 上の解答の赤字の部分は,
数学的帰納法の決まり文句です。
答案は、 この通りに つくっていけば、 OK です❗️
🌬️🏎️🌊 GIGAZINE 🌖🌙
2018年 1月16日 19時00分 叉兌 サエツ : サイエンス 🌙
キリスト教暦での、 第 千5百年代 な、 16世紀に
メキシコの アステカ文明を壊滅的な状況に追い込んだ伝染病の実態が
「 死者の歯 」 から浮き彫りに
By Siddie Nam
日本では、 戦国時代の真っ盛りであった、 1519 年 に
スペイン人の エルナン・コルテス が、 メキシコに上陸してから
数➕年の間に、 先住民族である アステカ人の間では
人類史上にて 最悪 とも言われる、 謎の伝染病がまん延して
壊滅的な状況に陥りました。
埋葬されていた 当時の死者の歯を調査したところ、 その原因は
「 サルモネラ菌 」 の ➖種であった
可能性が浮かび上がっています。
Salmonella enterica genomes from v ictims
of a major sixteenth-century epidemic in Mexico
|
Nature Ecology & Evolution
https://www.nature.com/articles/s41559-017-0446-6
A New Clue to the 1545 Cocolitzli Epidemic in Mexico -
The Atlantic
https://www.theatlantic.com/science/archive/2018/01/salmonella-cocoliztli-mexico/550310/
16世紀の メキシコ の 壊滅的な伝染病は
サルモネラ菌 が 原因 、 と考えられる
|
Nature Ecology and Evolution
|
Nature Research
http://www.natureasia.com/ja-jp/research/highlight/12328
この研究を進めたのは、
マックス・プランク・ヒト・サイエンス研究所の人類学者である
キルステン・ボス氏らによる研究 致廡 チム : チーム 。
伝染病で亡くなった住人の 歯の内部に含まれる
参封 サンプ➖ : サンプル 、 を分析することで
病原体の DNA を抽出し、
アステカ人を破滅寸前に追いやった原因を明らかにしています。
16世紀に メキシコに上陸した スペイン人は、
天然痘や 麻疹、 チフス ⚡️ などの
多くの病気を現地に持ち込んだ、 といわれており、
現地の人々は、 これらを総称して、 「 ココリツトリ 」
と呼んでいた、 とのこと。
1545年に、 最初の流行が発生し、 その後な、 1576 年に、 再び
被害が拡大します。
そのたびに、 数百万人単位の死者が続出し、
アステカ文明の人口は、 2000万人から 200万人へと激減した
とみられており、
その様子を目の当たりにした、 フランシスコ会修道士は
「 朝から夕方にかけて、 司祭たちは、 死体を運び、
それを溝に放り込んで埋めた 」 、 と記しています。
この ココリツトリ の詳細は、 これまでに、
ほとんどが、 明らかにされておらず、
天然痘 や 麻疹 などの 病気である、 と考えられてきましたが、
最新の DNA 分析 技術 を用いることで
その正確な姿が明らかにされてきています。
研究を行った ボス氏は、 メキシコの南部にある
大規模な ミシュテカ の 墓地に埋葬された 死者
11 人の歯 を取り出して、 その中に残された病原体の
DNA を詳細に調査しました。
🐉🌍🏝️ 『 RNA 疫鎮 問題⚡️ 』
:
【 遺伝子 : DNA : デオキシ リボ 核酸 、
らは、
毎日に、 いつでも、 色々な アミノ酸 たち から、
色々な タンパク質 らの 各々 を 作り出さしめる
仕事 ら を させられており
、
そのお蔭で、 我々なる 人 などの、
命 と 健康性 とが、 成し付けられ得て来てあり
、
準 遺伝子 とも 言うべき、
RNA : リボ 核酸 、 たちの内の
、
伝令 RNA : メッセンジャー RNA :
m RNA 、 たちの各々は
、
遺伝子 を 構成する
3つ で ➖つ の 並びよう な 塩基 らの
その 顔触れ に 対応せる
塩基 らを 自らの側に 揃 ソロ え
、
運搬 RNA : トランスファー RNA :
t RNA 、 をして
、
リボゾーム へ 持って行かせ
そこで、 その 塩基 ら の ➖つ ごと の 並びよう へ 対応する
➖種員 の アミノ酸 を 特定する
という事を繰り返して
色々な アミノ酸 たち から、 立体的に
特定の タンパク質 を 作り出さしめており
、
それらを 日常的に 成し行い付け得てある
のに対して
、
RNA ワクチン らは
、
その体の主の 遺伝性 らとは、
関係 が 無く⚡️
その主へ至る 累代員らの 可能的な 遺伝性 らへの
淘汰圧ら の 影響性 らに、
より、 関わり が 無い⚡️
が ゆえもあって
、
その体ごとの、 遺伝子らの、
より、 全体な 働き得ようらへ、
どんな 阻害性 の 影響性 らや
どんなに 余計な 過剰性 の 影響性 ら などを
与え付け得るか、 といった 向きの
可害 ベガイ : リスク 、 ら など を、
その宛ての 主らへ、 宛て付けるものでもある
ので
、
出来る得る限り、
我彼への その投与を避けて、
より、 質的な 栄養 らをの 充足 と
適度な 運動性 らとに よる
事の方が、
人々が、 その命と健康性とを成し付けるのに必要な
代謝 らを、
より、 漏れ⚡️ を 無しに、
成し付け得てゆくようにする上で、
より、 望ましい もの として、 ある☀ 】
歯の中の、 柔らかく生きている組織である 歯髄には
多くの血管が通っており、
血液の中に入り込んだ 病原体も、
もれなく、 歯髄の中に流れ込みます。
そして、 患者の死後には、
歯の外側にある、 硬い エナメル質 が
何世紀もの間にわたって、 病原体の DNA を保護する
役目を担う、 とのこと。
ボス氏は、 この血液の痕跡から、 DNA を抽出する
新しい技術を用いることで、 その病原体が
病原菌の➖種である、 サルモネラ菌の
DNA を 構成する、
塩基 配列 を持つ ことを発見しました。
By John Patrick Robichaud
この病原菌は、
「 チフス を引き起こす 細菌 」 を意味する
Salmonella enterica あるいは
S. enterica と呼ばれており、
今回に、 この菌が見つかったことで、
アステカ文明を破滅に追いやる原因の一つとなった伝染病は
チフス であったことを強く裏付けています。
さらに、 スペイン人が上陸する以前に死亡していた
5 人の 歯髄 参封 サンプ➖ には
S. enterica が 含まれていない ことも、
この説を裏付けるものとなっている、 とのこと。
チフス による 発熱は、
病気の人の糞便で汚染された ⚡️ 食物や水を介して広がるもので、
現代の社会では、 多くの人が密集している
貧しい環境で、 多くみられます。
論文では、 サルモネラ菌 が
他の病原体と相互作用した可能性がある
ことも 認めており、
今回に用いられた手法も、 その可能性を残すものである
とのこと。
この手法では、 DNA を検出することしかできない中で、
➖部の ウイルス は、
RNA で 分裂を行っている ことから、
今回の手法では、 見つけられなかった
他の要因があることを 研究 致廡 チム は、 認めています。
しかしながら、
古い DNA を用いた分析手法は、
これまで知ることができなかった
過去の状況を知る 手がかりになる ことが期待されています。
フランスの公立大学・エクス=マルセイユ大学の微生物学者、
ニコラス・ラスコヴァン氏は
「 この、 古い DNA に関する分野で、
新たな 捨歩 ステプ : ステップ は、
人間 への 共生物である 細菌 に
注目を集めることにつながるでしょう 」
と語っています。
















※コメント投稿者のブログIDはブログ作成者のみに通知されます