共時的構造と通時的構造、かなり前から使ってきたが、いま書いてみると手に馴染まなくなっている。
共時的構造とは、時間を固定して空間的な差異をみることによって出現する構造を指していた。これは時間を捨象しているから、単純に「場所的構造」とする。通時的構造とは、場所を固定して時間的な差異をみることによって出現する構造を指していた。これを「過程的構造」とよぶことにする。
波のグラフで説明してみよう。
位置(x)と媒質の変位(y)を表す波のグラフ(y-x図)では、ある時刻での波形が表される。これが場所的構造である。一方、時間(t)と媒質の変位(y)を表す波のグラフ(y-t図)では、ある位置の媒質の変位の時間変化が表される。これが過程的構造である。
「ひろがるかたち」(弁証法の場所的構造)
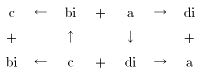
「つながるかたち」(弁証法の過程的構造)

共時的構造とは、時間を固定して空間的な差異をみることによって出現する構造を指していた。これは時間を捨象しているから、単純に「場所的構造」とする。通時的構造とは、場所を固定して時間的な差異をみることによって出現する構造を指していた。これを「過程的構造」とよぶことにする。
波のグラフで説明してみよう。
位置(x)と媒質の変位(y)を表す波のグラフ(y-x図)では、ある時刻での波形が表される。これが場所的構造である。一方、時間(t)と媒質の変位(y)を表す波のグラフ(y-t図)では、ある位置の媒質の変位の時間変化が表される。これが過程的構造である。
「ひろがるかたち」(弁証法の場所的構造)
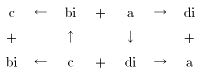
「つながるかたち」(弁証法の過程的構造)










