2 第4元kの場所
複素数が基礎である。iとi2の表示は次のようだった。
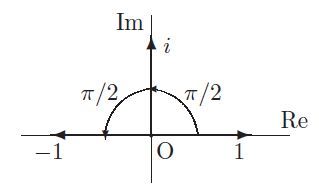
ハミルトンは複素数の二つの元1とiに対して垂直な第3の元jに気づく。
jとj2の表示は次のようだった。ここが出発点だった。
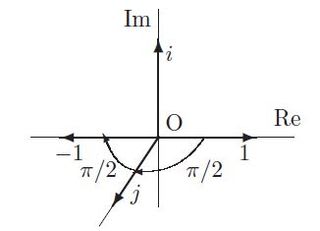
3元数の積(a+bi+cj)(x+yi+zj)は2つの原則(体の原則と絶対値の原則)にあてはまらない。ij=-ji=kの関係を満たす第4の元kを導入することによって、2つの原則は貫徹されるのであった。3元数は非合理だが、4元数として開くと合理的な数になるように思えたのである。
i2=-1,j2=-1を基礎にk2の値を調べてみると、
k2=(ij)2=ijij=-i(ij)j=-iijj=-i2j2=-1
である。i2=j2=k2=-1となり、虚数単位として整合的なのである。
では第4の元kはどこにあるのだろうか。

これは3元の図で1にkを重ねた図である。実軸は虚軸に隠れている。
立ち入ってみよう。
複素数が基礎である。iとi2の表示は次のようだった。

ハミルトンは複素数の二つの元1とiに対して垂直な第3の元jに気づく。
jとj2の表示は次のようだった。ここが出発点だった。

3元数の積(a+bi+cj)(x+yi+zj)は2つの原則(体の原則と絶対値の原則)にあてはまらない。ij=-ji=kの関係を満たす第4の元kを導入することによって、2つの原則は貫徹されるのであった。3元数は非合理だが、4元数として開くと合理的な数になるように思えたのである。
i2=-1,j2=-1を基礎にk2の値を調べてみると、
k2=(ij)2=ijij=-i(ij)j=-iijj=-i2j2=-1
である。i2=j2=k2=-1となり、虚数単位として整合的なのである。
では第4の元kはどこにあるのだろうか。

これは3元の図で1にkを重ねた図である。実軸は虚軸に隠れている。
立ち入ってみよう。









