B 対数の冪表示と級数表示(つづき)
注2
指数関数の級数表示を求める二項定理は高校以来の馴染みのものだが、対数関数の場合は、一般二項定理(自然数から実数に拡張したもの)である。
計算はややこしくなるが、考え方は同じである。
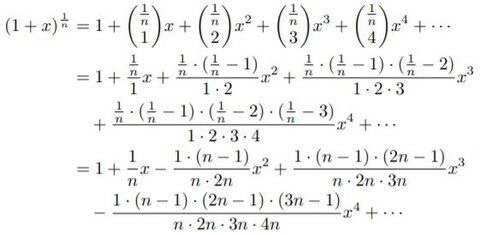
ここで、nは無限大数だから、

である。したがって、
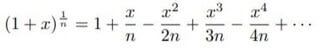
となる。nを両辺にかけると次のようになる。

したがって、log(1+x)は、

となる。これはメルカトルの公式である。
注2
指数関数の級数表示を求める二項定理は高校以来の馴染みのものだが、対数関数の場合は、一般二項定理(自然数から実数に拡張したもの)である。
計算はややこしくなるが、考え方は同じである。
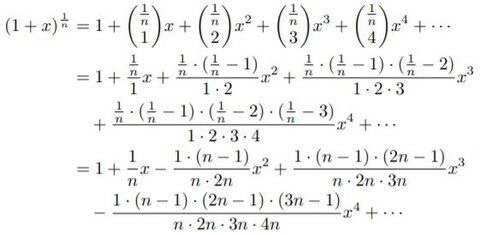
ここで、nは無限大数だから、

である。したがって、
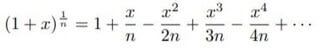
となる。nを両辺にかけると次のようになる。

したがって、log(1+x)は、

となる。これはメルカトルの公式である。









