オイラーは冪に着目して、
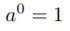
を起点に、一般的に指数関数と対数関数の冪表示と級数表示を導いた。
指数の冪表示から底aと数kの関係を導いて、k=1のときの底aをe(ネイピア数、自然対数の底)とした。
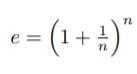

eを導入することによって、ヤコブ・ベルヌーイの無限複利法によるeの表示、 の無限級数表示、双曲線の下の面積(メルカトルの公式)を「算術的な世界」(志賀浩二)から把握した。これらは冪から構築した指数関数と対数関数を検証する道筋に位置づいている。
の無限級数表示、双曲線の下の面積(メルカトルの公式)を「算術的な世界」(志賀浩二)から把握した。これらは冪から構築した指数関数と対数関数を検証する道筋に位置づいている。
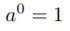
を起点に、一般的に指数関数と対数関数の冪表示と級数表示を導いた。
指数の冪表示から底aと数kの関係を導いて、k=1のときの底aをe(ネイピア数、自然対数の底)とした。
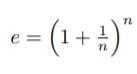

eを導入することによって、ヤコブ・ベルヌーイの無限複利法によるeの表示、
 の無限級数表示、双曲線の下の面積(メルカトルの公式)を「算術的な世界」(志賀浩二)から把握した。これらは冪から構築した指数関数と対数関数を検証する道筋に位置づいている。
の無限級数表示、双曲線の下の面積(メルカトルの公式)を「算術的な世界」(志賀浩二)から把握した。これらは冪から構築した指数関数と対数関数を検証する道筋に位置づいている。








