底aと底eの対数はそれぞれ次のようだった(底eのeは省略)。


ここで、1+x=aとおくと、
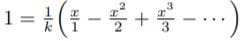

である。したがって、k=log aとなる。kは底aの自然対数に等しい。
これを任意の指数関数
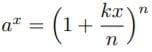
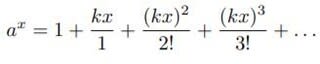
に入れると


となる。これが一般的な指数関数の冪表示と級数表示になる。
他方、任意の対数関数

に、k=log aを入れると、

となる。これが任意の対数関数の級数表示と自然対数の関係である。特に、a=10のとき、すなわち常用対数と自然対数の関係は次のようになる。

となる。ここでlog10の値は以前見たように、2.30258…である(1/log10は0.43429…となる)。


ここで、1+x=aとおくと、
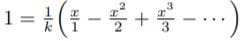

である。したがって、k=log aとなる。kは底aの自然対数に等しい。
これを任意の指数関数
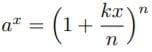
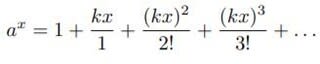
に入れると


となる。これが一般的な指数関数の冪表示と級数表示になる。
他方、任意の対数関数

に、k=log aを入れると、

となる。これが任意の対数関数の級数表示と自然対数の関係である。特に、a=10のとき、すなわち常用対数と自然対数の関係は次のようになる。

となる。ここでlog10の値は以前見たように、2.30258…である(1/log10は0.43429…となる)。









