しばらく前に高瀬正仁の本からオイラーの微分論の特徴を知った。無限小は0そのものであること、0/0の比は有限の値をもつことがあり、オイラーの関心はその有限値であったことなどである(この指摘に不定形のロピタルの定理が思い出されて感心した)。
オイラーの微分論に対してヘーゲルが次のように評価していることを最近知った。
(引用はじめ)『近代数学の発酵とヘーゲル弁証法』(本多修郎著、現代数学社、1989)
「オイラーはニュートンの一般的な定義を基礎にして微分計算が1つの大きさの増量の比例関係を考察したこと、しかし無限小の微差そのものは零とみなされるべきであることを要求した」。オイラーの方法では、関数y=f(x)におけるxの増分をhとし、後にh=0とおくのである。

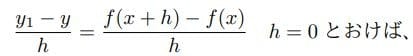

ヘーゲルは、オイラーがこの方法において増量の量的側面を零として無視し、その比だけを注目する態度を高く評価している。
(引用おわり)
つづく
オイラーの微分論に対してヘーゲルが次のように評価していることを最近知った。
(引用はじめ)『近代数学の発酵とヘーゲル弁証法』(本多修郎著、現代数学社、1989)
「オイラーはニュートンの一般的な定義を基礎にして微分計算が1つの大きさの増量の比例関係を考察したこと、しかし無限小の微差そのものは零とみなされるべきであることを要求した」。オイラーの方法では、関数y=f(x)におけるxの増分をhとし、後にh=0とおくのである。

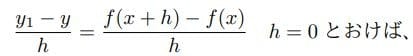

ヘーゲルは、オイラーがこの方法において増量の量的側面を零として無視し、その比だけを注目する態度を高く評価している。
(引用おわり)
つづく









