122節
この節はそのまま引用する(高瀬正仁訳)。
(引用はじめ)
対数系の作成にあたり、底aは意のままに受け入れることができるから、k=1となるように採ることも可能である。そこでk=1としてみよう。するとすでにみいだされた級数(§116)により、

となる。諸項を十進分数に変換して実際に加えると、aとして
2.71828 18284 59045 23536 028
という値が与えられる。この数値の一番最後の数字もまた正しい。
この底に基づいて対数を作成するとき、それらの対数は自然対数または双曲線対数という名で呼ぶ習わしになっている。というのは、双曲線〔とその漸近線で囲まれた部分〕の面積はこのような対数を用いて表示されるからである。表記を簡単にするために、この数2.71828 18284 59…をつねに文字
e
を用いて表わすことにしよう。したがって、この数は自然対数もしくは双曲線対数の底を表わしているわけであり、値k=1に対応することになる。言い換えると、この文字はeは無限級数
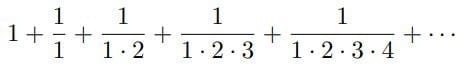
の和を表わしているのである。
(引用おわり)
§116の級数

この節はそのまま引用する(高瀬正仁訳)。
(引用はじめ)
対数系の作成にあたり、底aは意のままに受け入れることができるから、k=1となるように採ることも可能である。そこでk=1としてみよう。するとすでにみいだされた級数(§116)により、

となる。諸項を十進分数に変換して実際に加えると、aとして
2.71828 18284 59045 23536 028
という値が与えられる。この数値の一番最後の数字もまた正しい。
この底に基づいて対数を作成するとき、それらの対数は自然対数または双曲線対数という名で呼ぶ習わしになっている。というのは、双曲線〔とその漸近線で囲まれた部分〕の面積はこのような対数を用いて表示されるからである。表記を簡単にするために、この数2.71828 18284 59…をつねに文字
e
を用いて表わすことにしよう。したがって、この数は自然対数もしくは双曲線対数の底を表わしているわけであり、値k=1に対応することになる。言い換えると、この文字はeは無限級数
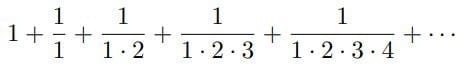
の和を表わしているのである。
(引用おわり)
§116の級数










