125節
底aと比kと変数zが満たすべき関係」(117節)は

だった。k=1のとき、底はeになるから、

となる。
オイラーは125節(7章最終節)でこの関係を確認して、まず、任意の指数関数の無限級数表示を示し、次に指数関数と対数関数の冪表示を導いている。
まず、

と置いて、両辺の双曲線対数をとると、log e=1より、

である。これをzに代入して、

となる。「任意の指数量が、双曲線対数の助けを借りて、無限級数を用いて書き表されることになる。」これは§117の級数表示(底a)でk=1としたものである(注1)。
次に冪表示を導いている。iを無限大数とすると、

であるから、

となる(注1)。
さらに、双曲線対数に対して、

という等式を示している。これは§119(底a)の冪表示でk=1としたものである(注2)。
注1(bをaに、zをyに置き換えて、)
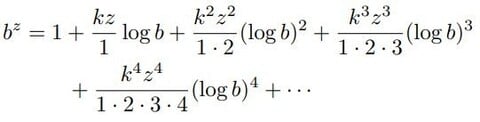

注2 ( )をつけて

底aと比kと変数zが満たすべき関係」(117節)は

だった。k=1のとき、底はeになるから、

となる。
オイラーは125節(7章最終節)でこの関係を確認して、まず、任意の指数関数の無限級数表示を示し、次に指数関数と対数関数の冪表示を導いている。
まず、

と置いて、両辺の双曲線対数をとると、log e=1より、

である。これをzに代入して、

となる。「任意の指数量が、双曲線対数の助けを借りて、無限級数を用いて書き表されることになる。」これは§117の級数表示(底a)でk=1としたものである(注1)。
次に冪表示を導いている。iを無限大数とすると、

であるから、

となる(注1)。
さらに、双曲線対数に対して、

という等式を示している。これは§119(底a)の冪表示でk=1としたものである(注2)。
注1(bをaに、zをyに置き換えて、)
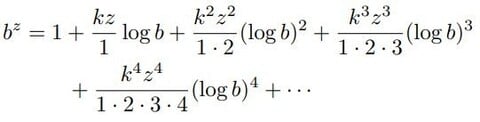

注2 ( )をつけて










