２つの線分が消えた理由3

山本義隆の楕円軌道発見の説明は誤っている。それはケプラーの図から2本の線分を消していることに端的に表れている。それは飛車と角を抜いて将棋を指しているようなもので、ケプラーの発見を構造的にとらえることはできない。

考えてみれば、ここはクライマックスと言っていいところで、山本の表現を借りれば「円軌道を放棄すると同時に、その円形性からの外れーー現代的に表現すれば対称性の破れーー」を洞察したところなのである。「正割」が「円軌道」に対応し、「円軌道の放棄」が「正割の代わりに」に対応している。「円形性からの外れ」が「正割の代りに半径を用いると観測結果のとおりとなる」に対応しているのである。
2本の線分を消すことによって「正割」も消えて、半径（直径距離）と観測結果の一致だけの指摘になり、矮小化された発見の説明になっている。それは『新天文学』第56章とは全く違っている。

こんど『世界の見方の転換』を通読していて、2本の線分を消したのは、切り取る三日月の幅を429に固定した結果ではないかという考えが浮かんできた。それが視覚的均差の位置を離心円から楕円にずらす結果をもたらしてしまい、そのためケプラーの正割（2本の線分）が不要になったのではないか。しかし、「正割」100429は否定できず、三角形の「正割」だけを取り上げて、100429と100000の関係を捏造したのではないかと考えてみたのである。
FA=FBsec(5°18′)=(1－0.00429) (1＋0.00429)a≒a=EB


次に浮かんできたのは、「面積法則」（第2法則）との関連が曖昧なのではないかという考えである。山本義隆は面積法則の説明で図12.9（「離心点に位置する太陽（A）からの距離と中心（B）から距離の比較」）を示している。

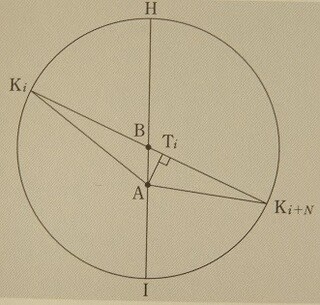
面積法則は離心円上の惑星の均一ではない速度の法則を把握するものである。ここで微小な扇形KiAKiを想定すれば、その面積はKiAに比例するのではなく、KiTiに比例するというのが面積法則発見の核心であるだろう。ケプラーは、この図のKiAをKiTiに置き換えることによって、円での単純な面積法則から離心円での面積法則を整合的に把握したのである。

これと同じことが楕円の発見でも起こった。KiAは「正割」である。KiTiは「半径（直径距離）」である。しかし、2本の線分がないため、この関連が断ち切られている。逆にいえば、 面積法則と楕円軌道発見の関連があいまいなため、2本の線分を消しても気にならなかったのである。

つづく