幻視のなかの橋4

4　i²=j²=k²=ijk=-1

ij=-ji=kからどのようにして基本公式
i²=j²=k²=ijk=-1
が出現したのだろうか。
出発とするのはi²=j²=-1が示されている次の図（矢野忠『四元数の発見』参照）である。

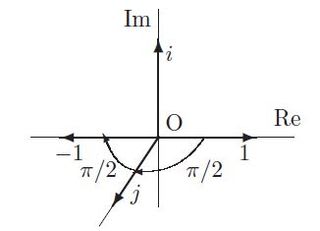
ここでは3次元で3つの元(1,i,j)が示されている。ここにはまったく歪みはない。
1-i-i²は、垂直の平面を回転して-1に達する。
1-j-j²は、水平の平面を回転して-1に達する。
ここに第4の元kが付け加わえる。

ここでkはij=-jiによって生成したものである。実軸の1に重ねてkを示し、実軸に虚軸を重ねている。他方、実軸の負の方向は出発点のままで-1を残している。いいかえればこの図は歪んでいる。しかし、基本公式に出てくるi,j,k,-1は過不足なくすべてそろっている。ここを足場にする。
1-k-k²の回転はこの図のなかでは見えない。垂直でもなければ水平でもない、いわば斜面を回るのである。この回転を幻視する。もちろんこの回転は見えない。しかし、その回転の影は見えるのである。その影とは、i²=-1,j²=-1である。ijk=k²がi²とj²と同時に-1に達したとき、基本公式が誕生した。
1　
ij=-ji=kよりijk=k²が導かれる。
ij･(-ji)
=ijk
=(ij)k
=k²
2
k²とi²=-1,j²=-1の関連が洞察される。
k²
=ij･(-ji)
=ijij
=-i(ij)j
=-iijj
=-i²j²
ここで、i²=-1,j²=-1より、
k²
=-(-1)(-1)
=-1
3
すべての「虚」が「実」に変換される。
i²=j²=k²=ijk=-1