「論理的なもの」の表出論4

（「論理的なもの」と複素平面）

　「論理的なもの」の表出論の特徴は複素数をモデルとしていることである。複素数はa＋bi（実部と虚部）という構造をもっている。これまで「論理的なもの」の２つの側面（自己表出と指示表出）を実部と虚部にそれぞれ対応させてきた。すなわち、
　　「論理的なもの」＝「自己表出」＋「指示表出」i
と考えてきた。
　これまで自己表出を実部に、指示表出を虚部に対応させてきたのは、すでに把握されている「論理的なもの」を前提としていたからである。「論理的なもの」の内部においては理性の推論が実質を担っており、外部（認識対象）と関係する悟性は「想像されたもの」と位置づけるのが、自然と思われたからである。（この「悟性」は変容する可能性がある。）
　しかし、これから新しく把握しようとする「論理的なもの」においては、こんどは逆に、出発点となる悟性が実質で、「論理的なもの」の内部の理性の推論は「想像的なもの」と位置づける方が妥当だと思われる。つまり、実部に指示表出を対応させ、自己表出に虚部を対応させる方が自然と思われる。つまり、
　「論理的なもの」＝「指示表出」＋「自己表出」i
と考えるのである。
　これは「論理的なもの」を前提としないときの対応だが、２つの「論理的なもの」（AとA’）から1つの「論理的なもの」（B）をつくる過程においても、新たな1つの「論理的なもの」は、途中から生まれてくるのではなく、最初から形成され始めていると考えれば、
　「論理的なもの」＝「指示表出」＋「自己表出」i
という対応の方が根源的ではないかと思う。
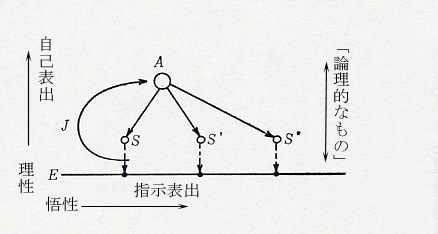
　指示表出は実部と対応する。自己表出は虚部と対応する。ガウスの複素平面の実軸は水平軸であり、虚軸は垂直軸である。アインシュタインの思考モデル（1952年）に投影した「論理的なもの」の背景には複素平面があるといえよう。