2元数と3元数

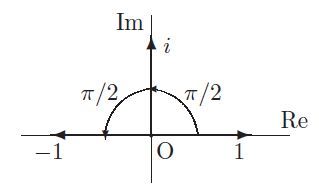
複素数の二つの元1とiは次のように表示される。元1を原点Oを中心にしてπ/2=90°回転すると元iが得られる。さらにiをπ/2=90°回転すると-1が得られる。複素数（2元数）a+biは実軸Re(x軸)、虚軸Im(y軸)の平面上の点(a,b)を表わす。

ハミルトンは複素数の二つの元1とiに対して垂直な第3の元jに気づいた。iがxy平面を回転するのに対して、jはxz平面を回転して－1になる。j²=-1である。j²=i²だが、jはiではない。3元数a+bi+cjは実軸Re(x軸)、虚軸Im(y軸)、虚軸I'm(z軸)の空間の点(a,b,c)と対応するのではないか。これがハミルトンの出発点だった。

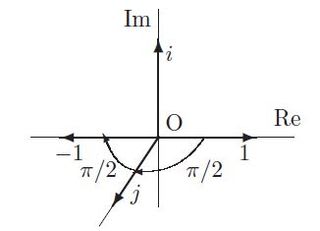
図は矢野忠「四元数の発見へ」（『数学・物理通信』1巻11号）より