内積と外積の幾何

四元数の純虚数部は3次元（i,j,k）だが、2元（i,j）だけを考える。いいかえれば空間ベクトルではなく平面ベクトルを考える。
z=ai+bj
w=xi+yj
いま、z,wを極形式で表わすと、
z=r(icosθ+jsinθ)
w=s(icosφ+jsinφ)
r,sは絶対値、θ,φは偏角である。

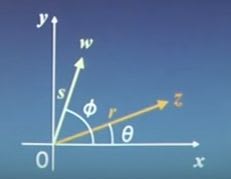
（「ハミルトンとベクトルの誕生２ー内積・外積の起源と仕組み」より）
zとwの積を計算する。
zw=rs(icosθ+jsinθ)(icosφ+jsinφ)
=-rs(cosθcosφ+sinθsinφ)
+rs(cosθsinφ-sinθcosφ)k
i²=j²=-1,ij=-ji=kを使った。加法定理より、zとwの積は
zw=-rscos(φ―θ)+rssin(φ―θ)k
前の下線が内積である。後の下線が外積である。外積はベクトルだが、それはkによって表示されている。kは画面に垂直な方向である。
zw=(ai+bj)(xi+yj)
=-(ax+by)+(ay-bx)k
より
内積rscos(φ―θ)=ax+by
外積rssin(φ―θ)k=(ay-bx)k
である。