等化点Eはどのように見いだされたのか。山本義隆は『世界の見方の転換』1の付記「金星の軌道パラメータの決定」において、問題は等化点を見いだすことにあるとして、次のように答えている。山本の説明を確認しておこう。
(引用はじめ)
他方、第一の不等性は、地球から見て周転円の中心の運動が一様でないことによる。それをプトレマイオスは長軸線上の別のある点の周りに等角度で回転している結果として説明する。したがって問題はその点すなわち等化点Eを見いだすことにあるが、それは次のようになされる。
平均太陽は一定の角速度で回転するのであるから、それはこの点Eから見た回転を表し、したがって角度θは春分点方向とEQの方向のなす角であり、∠QEA=θ-λa。
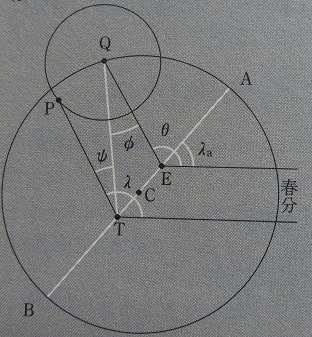
ここで図のように任意の時刻の惑星の位置をP、周転円の中心をQとして、∠EQT=φ、∠QTP=ψとすると、図より惑星Pの黄経はλ=θ-φ+ψ。
さて、ここで特に表のD7とD8の場合を考える。

この二つはθが等しいのでQは同一の地点であり、それゆえ、φの値も等しく、さらには
この結果より、 ET =2 CT 、すなわち、長軸線上で地球Tの位置する離心点Fと等化点Eの中点に誘導円の中心Cがある(離心距離の二等分)。
(引用おわり)
注1
∠P8TQはわかりやすいと思うが、∠TQEの方はわかりにくいと思う。直感的にとらえにくい。
λ=θ-φ+ψより、ψ=φ-θ+λ。
したがって、
ψ7=φ7-θ7+λ7
ψ8=φ8-θ8+λ8
これをψ7=-ψ8にいれて、
φ7+φ8=θ7 -λ7+θ8+λ8
φ7=φ8=φだから
左辺は2φ
整理して
-2φ=(λ8-θ8)+(λ7-θ7)
なおλ8-θ8=+48+1/3(東方最大離角)、λ7-θ7=―43―7/12(西方最大離角)。
注2
直角三角形TQP8において、TQを周転円の半径cと∠P8TQで表す。
注3
直角三角形TQEにおいて、TEをTQと∠TQE(=φ)で表す。
注4
TQを媒介にして周転円(Q)と離心円(T,C,E)を結び付けている。
(引用はじめ)
他方、第一の不等性は、地球から見て周転円の中心の運動が一様でないことによる。それをプトレマイオスは長軸線上の別のある点の周りに等角度で回転している結果として説明する。したがって問題はその点すなわち等化点Eを見いだすことにあるが、それは次のようになされる。
平均太陽は一定の角速度で回転するのであるから、それはこの点Eから見た回転を表し、したがって角度θは春分点方向とEQの方向のなす角であり、∠QEA=θ-λa。

ここで図のように任意の時刻の惑星の位置をP、周転円の中心をQとして、∠EQT=φ、∠QTP=ψとすると、図より惑星Pの黄経はλ=θ-φ+ψ。
さて、ここで特に表のD7とD8の場合を考える。

この二つはθが等しいのでQは同一の地点であり、それゆえ、φの値も等しく、さらには
θ-λa=(270+1/2)°≒3直角ゆえ、直線EQは長軸線ABに直交している。しかもD7 は西方に、D8は東方に平均位置から最も離れた場合であるから(中略)、対称性よりψ7=-ψ8。したがって(注1)
∠TQE=-φ=1/2・(λ8-θ8+λ7-θ7)=(2+3/8)°また
∠P8TQ=(∠P8T P7)÷2=1/2・{(λ8-θ8)-(λ7-θ7) }=(45+23/24)°ところが TQ sin(∠P8TQ)= QP8 =cゆえ(注2)
TE = TQ sin|φ|=csin(2+9/24)°/sin(45+23/24)°=0.0415a=2ea(注3,4)ここに(中略)e(=0.0213)とc(=0.720a)の値を使った。
この結果より、 ET =2 CT 、すなわち、長軸線上で地球Tの位置する離心点Fと等化点Eの中点に誘導円の中心Cがある(離心距離の二等分)。
(引用おわり)
注1
∠P8TQはわかりやすいと思うが、∠TQEの方はわかりにくいと思う。直感的にとらえにくい。
λ=θ-φ+ψより、ψ=φ-θ+λ。
したがって、
ψ7=φ7-θ7+λ7
ψ8=φ8-θ8+λ8
これをψ7=-ψ8にいれて、
φ7+φ8=θ7 -λ7+θ8+λ8
φ7=φ8=φだから
左辺は2φ
整理して
-2φ=(λ8-θ8)+(λ7-θ7)
なおλ8-θ8=+48+1/3(東方最大離角)、λ7-θ7=―43―7/12(西方最大離角)。
注2
直角三角形TQP8において、TQを周転円の半径cと∠P8TQで表す。
注3
直角三角形TQEにおいて、TEをTQと∠TQE(=φ)で表す。
注4
TQを媒介にして周転円(Q)と離心円(T,C,E)を結び付けている。










