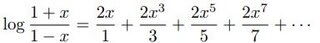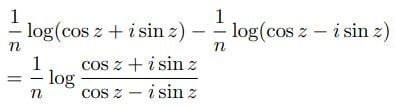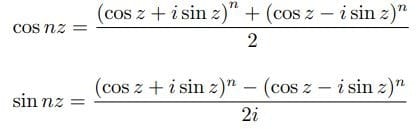イロハモミジが色づいてきている。近づいてみると、紅葉が始まったばかりだった。

イロハモミジ(いろは紅葉)の名は、手のひらのように裂ける葉の裂片(指)を、いろはにほへと……数えたことに由来するという。色づいた指が、い、いろ、いろは、いろはに、ほとんどが青いままである。紅葉は始まったばかりである。色も鮮やかとはいいがたい。

イロハモミジ(いろは紅葉)の名は、手のひらのように裂ける葉の裂片(指)を、いろはにほへと……数えたことに由来するという。色づいた指が、い、いろ、いろは、いろはに、ほとんどが青いままである。紅葉は始まったばかりである。色も鮮やかとはいいがたい。











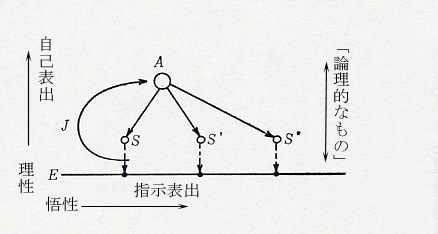




 について解いていくと次のようになる。
について解いていくと次のようになる。


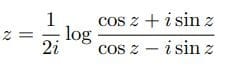
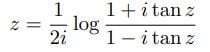 (1)
(1)