寄り道ばかりで、中々前へ進まない「ガロアを巡る旅」ですが。前々回”その13”では、複素数つまり負の平方根(虚根)を巡る長い歴史について述べました。
今日は長くなりますが、前半は複素平面に関する簡単なテーマですので、軽く流す様に読んでください。
この負の平方根を認めるキッカケとなったのが、3次方程式の研究からでした。
例えばx²+1=0の解は、−1の平方根ですが数直線上にはないので、”解なし”で済ませてきました。故に、負の平方根を考えるキッカケにはならなかった。
しかし、ある3次方程式では解が実数にも関わらず、それを表記しようとすると負数の平方根は避けられなくなる。
例えば、x³−6x+2=0の解の1つは、当時知られていたフォンタナの公式(”その7”参照)によれば、解の1つはα=−³√(1+√(−7))−³√(1−√(−7))というグロテスクな数になる。
そこで当時の数学者たちは、√(−7)という負の平方根を実数の形で表そうとするが、尽く分厚い壁に弾かれます。
ここで”数学の巨人”ガウスの登場です。
ガウスは、”(実係数の)3次方程式を解く上で負の平方根は避けられない”事を証明しました。
そこで数学者は仕方なく、負数の平方根を”虚数”(imaginary number)とし、その虚数を全て含む様な体を”複素数”と名付けます。
因みに、1637年にルネ・デカルトは、この複素数の虚部をNombre imaginaire(想像上の数)と名付けた。
x²+1=0の解は、今では±iと”虚数単位”として表記されますが、双方とも大きさが同じで代数的には区別が付きません。
しかし、これこそが”体の自己同型として現れ、対称性の源と”なり、”虚数解を許せば、全ての方程式は解ける”というガウスの偉業に繋がったのです。
この虚数iから、R(i)=(実数)+(実数)iという数の集合である複素数体R(i)を作るんですが、”全てのn次方程式は、R(i)の中に全ての解が含まれる”事をガウスは証明しました。
複素数の世界とその起源
”その13”でも述べた”複素数体”を理解するには、複素数の世界を目で見える様にする必要がある。つまり、四則演算で複素数の描く図形はどんなものか?
これにはノルウェーの数学者カスパー・ベッセル(1745-1818)とガウス(1777-1855)の2人の数学者が独立に成功します。
因みに、複素平面(複素数)が世に出たのは、1797年のベッセルの論文が最初とされるが、デンマーク語で書かれ、デンマーク以外では読まれず、1895年にようやく発見された。
一方ガウスは、1796年以前に既に複素平面の考えに到達してた。当時、虚数は数学者の間ではタブーとされ、ガウスは持論である複素平面図を隠し続けてたんです。
1831年に、機は熟したと見たガウスは複素平面を論じ、複素数は複素平面として知られる様になる。ここに、虚数に対する否定的な視点は完全に取り除かれ、複素数が受け入れられていく(Wiki)。
複素数”a+bi”を座標(a,b)の位置に置く事で、複素数は全て平面上を支配する。故に、複素平面として知られる様になるが、何か利点がなければ、このアイデアは歴史の中で埋没してた筈です。
その利点こそが”四則演算が図形的な意味を持つ”という事でした。
まず、複素数の足し算を考えます。
(a+bi)+(c+di)=(a+c)+(b+d)iをx,y座標で見れば明らかな様に、点(0,0)(a,b)(c,d)(a+c,b+d)の関係は平行四辺形を描いてます。
複素数の演算と複素平面
次に、複素数の掛け算です。これは足し算のように簡単じゃない。
例えばc+diに実数2を掛けると、(c,d)は(2c,2d)に延長します。故に、足し算と実数倍が出来るから複素数は実数体上のベクトル空間とみなせます。
”その8”でも説明した様に、(2次元)ベクトル空間とは任意の2点を足し算と実数倍で全ての点を作り出す事でした。
しかし、虚数iを掛けるとどうなるのか?
i×(c+di)=ic+di²=(−d)+ci。これは点(c,d)が(−d,c)に置き替えられ、座標で確認すれば、点(c,d)を原点を中心に左周りに90度回転した点(−d,c)になる。
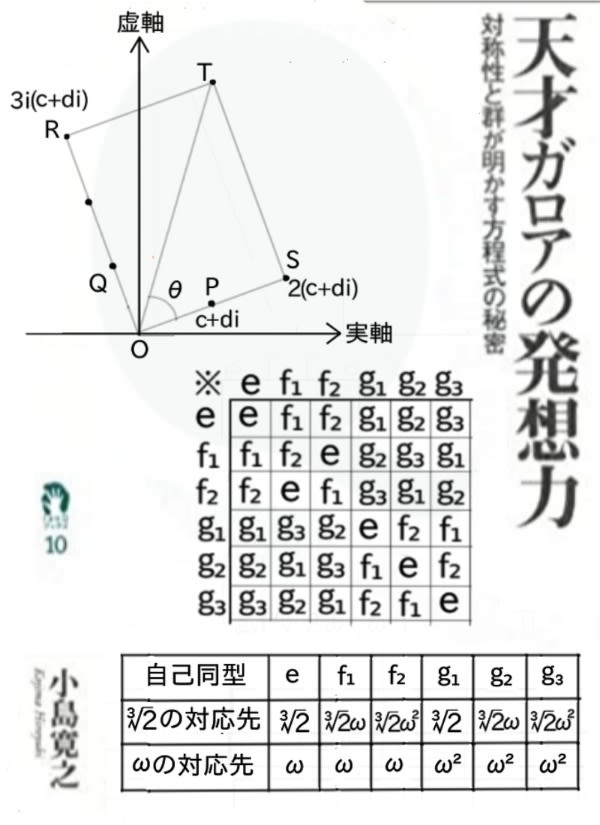
では、任意の複素数(c+di)に特定の複素数(2+3i)を掛ければどの様な位置に動くのか?
(c+di)×(2+3i)=2(c+di)+3i(c+di)
2(c+di)は上で述べた様に、点P(c,d)の複素数を原点と結んで2倍にした、点S(2c,2d)の位置の複素数になる。また、3i(c+di)は点Pを減点を中心に左回りに90度回転した点Q(−d,c)のいちの複素数を、更に3倍に延長した点R(−3d,3c)の複素数となる。3i(c+di)=−3d+3ciより明らかです(イラスト参照)。
故に、この2つの和=2(c+di)+3i(c+di)は、原点Oと点Rと点Sで作った長方形の残る頂点Tの位置の複素数となる。これは複素平面がベクトル座標となる事から明らかですね(イラスト)。
つまり、この長方形は元の複素数(c+di)が何であっても、辺の比が常に2対3であるから、相似形な長方形となります。
故に、点Pの任意の複素数(c+di)に(2+3i)を掛ける事で移動する点Tは、原点に対しPを一定の角(θ)回転し、原点から一定倍率(OT/OP)だけ拡大した点である事が解る(イラスト)。
当然これは、(2+3i)だけでなく一般の(a+bi)にても同じ事が成立します。そこで、以下の事が言える。
”任意の複素数に特定の複素数(a+bi)を掛けると、原点を中心に左回りに回転した位置に複素数が出来る。その時、回転角θは(a+bi)とx軸とのなす角であり、拡大率は(a+bi)と原点を結んだ線分の長さである”
以上より、複素平面が非常にきれいな性質を持つ事が判りました。足し算と掛け算を例にしましたが、引き算も割り算も少しややこしいですが、同様にきれいな性質を持つ事は明らかです。
つまり、複素平面上では足し算(引き算)は平行移動で、掛け算(割り算)は回転拡大(縮小)となります。
n乗根と正n角形の密な関係
複素平面の美しい図形は、xⁿ=1の解である”1のn乗根”(べき根)の世界でも披露されます。
n=4の時をまず例にとれば、x⁴=1はx⁴−1=(x²−1)(x²+1)=(x+1)(x−1)(x+i)(x−i)=0より、”1の4乗根”は±1、±iとなる。
この4つの数を複素平面上に配置すると、正方形をなり、”1の4乗根は正方形を作る”。
これは偶然なのか?必然なのか?
答えは勿論、必然です。
4つの解は、+1にiを1個,2個,3個,4個掛ければ得られます。(+1)×i=i、(+1)×i×i=−1、(+1)×i×i×i=−i、(+1)×i×i×i×i=+1より明らかですね。前述した様に、”iを掛ける事は原点に対し左回りに90度回転”でしたから、4つの”1の4乗根”は(1,0)→(0,1)→(−1,0)→(0,−1)と正方形を描く。
逆を言えば、”1の4乗根”は360度を4等分し90度を求め、原点に対し90度回転した複素数はiだから、i=i、i²=−1、i³=−i、i⁴=+1を得る事で求まる。つまり、+1を0度、90度、180度、360度回転した事を意味するから、これらの値が”1の4乗根”の全てとなる。
以上の事は、”1のn乗根”でも同様に成立します。
まずθ=360/nを求め、次に原点に対し左回りに(+1)をθ回転した位置の複素数αを求め、”1のn乗根”である複素数α¹,α²,・・・,αⁿを求める。
但し、複素数α¹,α²,・・・,αⁿは全て原点からの距離は常に1のままで、半径1の円周上に等間隔で並ぶ。故に、”n個の1のn乗根”を複素平面に配置すれば正n角形を描くという事。
これを利用し、”1の3乗根”を求めます。
θ=360/3=120度。次に、原点に対し120度回転した複素数αは、ω=−1/2+i√3/2となる。α²は更に120度回転した位置にあるので、ω²=−1/2−i√3/2。それとω³=1が残る1つです。図(”円分方程式”を参照)を見れば、正三角形になってますね。
事実、x³−1=(x−1)(x²+x+1)=0より、この解はx=1、(−1±√(−3))/2となる。
べき根を加えた体とは?
そこで、xⁿ=aという方程式の複素数解を有理数に加えた体について分析します。
まず、x³=1の解ωを有理数に加えた体Q(ω)を考える。ωはx²+x+1=0の解ですから、”その9”でも述べた様に2次体の一種で、Q(ω)=”(有理数)+(有理数)ω”という形になります。
体の性質は実数でも複素数でも変わりないので、Q(ω)の自己同型はの2種類でしたね。1つは恒等写像eで、もう1つはωとω²を入れ替える共役写像fでした。
この2つの自己同型は群{e,f}を作る。乗積表で見れば、2等辺3角形の対称操作の群と同型です(”その9”参照)。
次に、x³=2の解を考えます。1と2の間に解があり、その解を2の立方根と呼び、³√2と記す。この記号を使えばx³=2は、両辺を2で割り、2=(³√2)³より、(x/³√2)³=1いう形になる。
x³=1の解ωを使えば、x/³√2=1、ω、ω²となり、x³=2の解は³√2、³√2ω、³√2ω²となりますね。これらを”2の3乗根”と呼ぶ。
そこで、x³=2の解の1つの³√2を有理数に加えた体Q(³√2)を考える。
(³√2)³=2から、この体の形は”(有理数)+(有理数)³√2+(有理数)(³√2)²”と見抜けます。
しかし、自己同型という点で見れば大きな問題が起きる。自己同型は四則演算を保存し(有理数を)不変にするので、f((³√2)³)=f(2)から(f(³√2))³=2となる。
故に、fにより³√2が対応するのは、³√2,³√2ω,³√2ω²の何れかで、これはx=f(³√2)とおけばx³=2となり明らかです。
だが、³√2ωと³√2ω²はQ(³√2)の元ではないから、解と体の関係が崩れる。
体を拡大するとは?
この混乱を防ぐ為には2つの手法がある。1つは体を作る時に、x³=2の1つの解³√2だけじゃなく全ての解を加える。もう1つは、解を加える体を有理数Qではなく、”有理数に1の3乗根を加えた体”F(³√2)にする。
ここでは前者を考えます。そこで、有理数にx³=2の全ての解を加えた体は結局は有理数に³√2とωを加えた体となる。
この体をKとすると、Kの自己同型fは³√2とωをKのどんな数に対応させるかによって決まります。
³√2が対応するのは³√2,³√2ω,³√2ω²の何れかでした。また、ωとω²はx²+x+1=0の解だから、ωが対応するのはωかω²となる。
故に、この組合せは全部で3個(³√2,³√2ω,³√2ω²)×2個(ω,ω²)=6通りになる。そこで、体Kの自己同型(写像)の6つをe、f₁、f₂、g₁、g₂、g₃とすると、6つの自己同型による³√2の対応先とωの対応先は、e(³√2,ω)→(³√2,ω)、f₁(³√2,ω)→(³√2ω,ω)、f₂(³√2,ω)→(³√2ω²,ω)、g₁(³√2,ω)→(³√2,ω²)、g₂(³√2,ω)→(³√2ω,ω²)、g₃(³√2,ω)→(³√2ω²,ω²)(対応表も参照)。ここ少し修正です。
以上より、体Kの自己同型のなす群G={e、f₁、f₂、g₁、g₂、g₃}となりますね。
では、これらの群の組合せがどんな構造になってるのか見てみよう。
まず、f₂※f₁の自己同型を調べるには、³√2とωの各々の対応先を見ればいい。
f₂※f₁(³√2)=f₂(f₁(³√2))=f₂(³√2ω)=f₂(³√2)f₂(ω)
=³√2ω²ω=³√2。また、f₂※f₁(ω)=f₂(ω)=ω。故に、上の対応からf₂※f₁=eとなります。
次に、f₁※g₁(³√2)=f₁(g₁(³√2))=f₁(³√2)=³√2ω。また、f₁※g₁(ω)=f₁(ω²)=f₁(ω²)=(ω)=f₁(g₁(ω))
=f₁(ω²)=f₁(ω²)=f₁(ω)f₁(ω)=ω²。故に、f₁※g₁=g₂となる。
因みに、体Kのfは積(四則)に関して閉じてるので、f(xy)=f(x)f(y)でしたね。
以上より、{e、f₁、f₂、g₁、g₂、g₃}の全ての演算結果を乗積表に作れば、上のイラストの様になります。
この乗積表は、”その10”で紹介した正三角形の対称操作の群{e,f₁,f₂,g₁,g₂,g₃}の乗積表と全く同じものとなる。つまり、正三角形の対称操作の群と同型という事ですね。
以上で、方程式を分析する土台となる複素数と、”方程式が四則とべき乗で解ける”ガロア理論の根幹をなす”複素数解を有理数に加えた体”の準備が出来ました。
かなり長くなりましたが、後半の”べき根を加えた体の拡大”についての理解が少しややこしいですが、この拡大体の考え方こそがガロア理論の中核なんですね。
次回は、3次方程式が解けるカラクリについて述べたいと思います。










🌸大変よく出来ました🌸
次回は自己同型群と正規部分群の関係について述べますが。
これがまたまた抽象的すぎて、書いてる最中は解ったつもりですが、後から眺めると???なんですよね。
そして可解群になるためには
方程式の係数と解を目一杯詰め込んだ拡大体が自己同型になってることを示せばいいのかな
抽象過ぎてそれ以上は???だけど
書いてる転んだサンはもっと大半なのよね
拡大体の自己同型群の要素同士の演算結果を1つ1つ調べ上げ、乗積表にし対称操作の群と同型である事を確認するんですが。「天才ガロアの発想力」には誤植も幾つかあり、1つ1つ吟味するのに大変でした。
そういう私も疲れました👅
コメント有り難うです。
転んだ君がやったように、拡大体が自己同型群になってるかは、拡大体の各要素の演算が全単射になってるかを示せば良いわけで、それが崩れたら拡大体はガロア群にはなりえない。しかし1つ1つ調べ上げ、1つでも拡大体をはみ出したら終わりなんだよな。
ここは非常に根気のいる作業で、読んでてこっちも疲れたさ。
<ガロア群が可解群となる>ことが終着駅なんだけど、そこまでに到達するのが・・・