
ドローンを使って地表を撮影し、Civil3Dで作図するシーンをイメージして以下の質問を思い付いた。
以下は、任意の曲面をフーリエ変換するPythonプログラムの例です。numpyとmatplotlibのライブラリを使用しています。このプログラムでは、フーリエ変換を2回実行して、元の曲面と復元された曲面を比較します。
import numpy as np
import matplotlib.pyplot as plt
# 2次元フーリエ変換
def fft2d(surface):
return np.fft.fft2(surface)
# 逆2次元フーリエ変換
def ifft2d(fourier_surface):
return np.fft.ifft2(fourier_surface)
# メイン関数
def main():
# 曲面を生成する
x = np.linspace(-10, 10, 256)
y = np.linspace(-10, 10, 256)
xv, yv = np.meshgrid(x, y)
surface = np.sin(np.sqrt(xv ** 2 + yv ** 2)) / np.sqrt(xv ** 2 + yv ** 2)
# フーリエ変換する
fourier_surface = fft2d(surface)
# フーリエ逆変換して元の曲面を復元する
restored_surface = ifft2d(fourier_surface).real
# 結果をプロットする
fig, axs = plt.subplots(1, 2, figsize=(8, 4))
axs[0].imshow(surface, cmap="gray")
axs[0].set_title("Original Surface")
axs[1].imshow(restored_surface, cmap="gray")
axs[1].set_title("Restored Surface")
plt.show()
if __name__ == "__main__":
main()
このプログラムは、-10から10までの範囲のxとyの値を持つ256x256のメッシュグリッドを作成し、それに対してsin(sqrt(x^2 + y^2))/sqrt(x^2 + y^2)を適用して、曲面を生成します。その後、生成された曲面に対して2次元フーリエ変換を実行し、フーリエ逆変換によって復元された曲面を計算します。最後に、元の曲面と復元された曲面を2つのサイドバイサイドのサブプロットでプロットします。
以下はPydroidでの実行結果
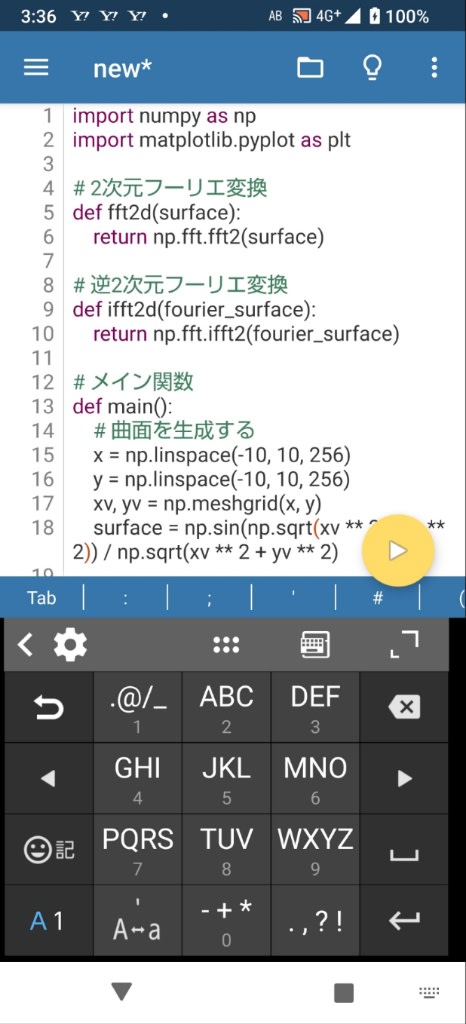
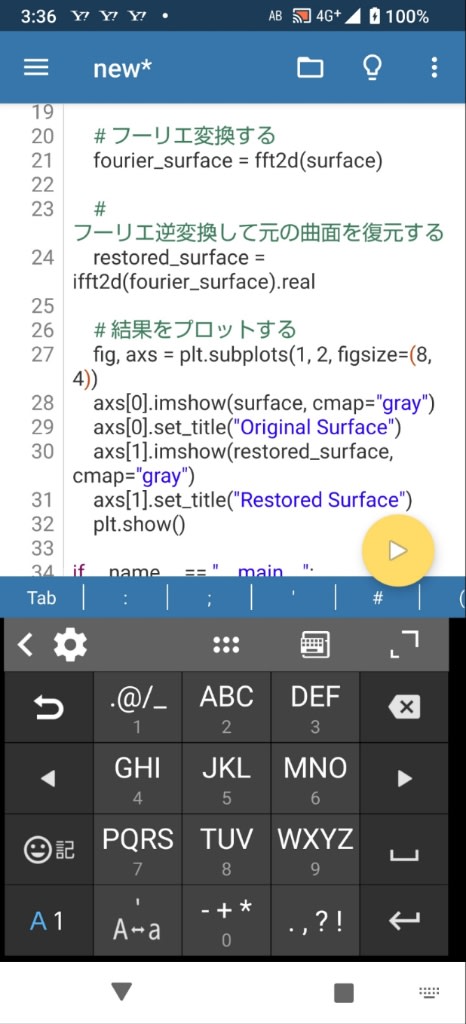


ドローンで地表を撮影した際に得られた高低差のデータを利用して加工すれば、Civil3Dに自動で作図させることも可能になると思われる。



















