回したり、切ったり、貼ったり、・・・円は 不思議～

前回の問題

色の付いた部分の面積ですが、円の面積から中の正方形の面積を引けばいい！

ということになりますが、・・・

中の正方形の面積は？一辺の長さは？

というと、どうしましょう？

 

こうしましょう～ 円をぐるっと回してみると

このように、なります。（書いてある物は、回らないよ～）

（そういうときは、頭の中で想像するか、自分で書いてみてください）

中の正方形の一辺の長さは、小学生にはムツカシイのですが

面積だったら、外の正方形の半分だ！ってことは分かります。

（中の正方形の対角線を２本書いてみてください）

（ひし形と同じように考えれば、面積は縦×横÷２）

そうしますと、これはもうしめたもので、

円の半径５ｃｍ、円の面積は５×５×３．１４

中の正方形の面積は、１０×１０÷２

よって色の付いた部分の面積は

５×５×３．１４－１０×１０÷２＝２８．５     ２８．５平方センチメートル

 

 

もう一つの問題

この色の付いた部分の面積は？

もし、五角形がなければ、円が５つ分で計算はカンタンですね。

ところが、この五角形が円の一部の扇形を隠しているから

ややこしくなる～

こんな時は、全部まとめて考えましょう～

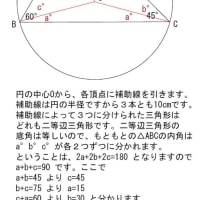
五角形が隠す扇形をすべて集めると、

円が何個分になるのか？を考えます。

これは、扇形の角度の合計が分かればいいので

五角形の内角の合計と同じになりますから

１８０°×３  （五角形は、三角形×３つで作れます。１つの頂点から対角線が２本引けます）

これは、半円が３つ分の角度ですね。

（ここで、１８０×３を計算してしまうと、後でまた割り算をすることになります）

と言うことは、円が１．５個。これを引けばいいので

色の付いた部分の面積は

円５個分－円１．５個分    円の半径は１０ｃｍでしたね

１０×１０×３．１４×（５－１．５）＝１０９９       １０９９平方センチメートル

 

今回の２つは、定番の問題ですから

考え方を覚えておけば、数値が変わっても大丈夫。

五角形が、四角形や三角形になっても大丈夫。

 

内角の和   と   外角の和

復習しておいてください～