2次関数と1次関数 グラフで考える～

前回の問題、2次関数と1次関数の X と Y の 変域が同じ！という場合は

その変域を長方形で囲むことができます。

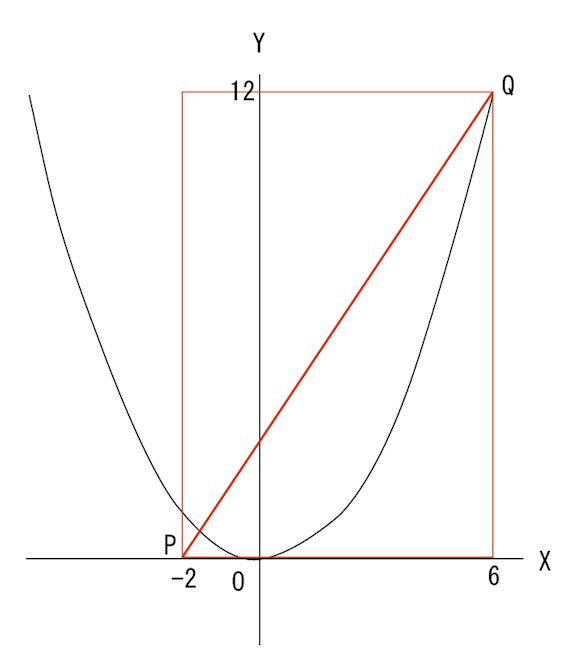
これは、Xの変域が－２から６まで、

そのときのYの変域は、2次関数の式から ０から１２まで。

ここで大事なことは、2次関数の変域は最小が０であることです。

こうしてXとYの変域をグラフに長方形で書きますと

図のようにピンクの四角形になります。

1次関数のXとYの変域も これと同じということは

この変域（ピンクの長方形）の対角線になります。

1次関数  Y=ｂX＋ｃ  （ｂ＞０）  ですから

ｂは12/8=3/2

cは ３  だと図から分かります。

計算で求める場合は、Pの座標と  Qの座標を使って

－２ｂ＋ｃ＝０

６ｂ＋ｃ＝１２

の連立方程式を解くという方法もあります。

 

一見むつかしそうな問題でも、考え方が分かっていると

（過去に同じ問題を解いた経験があると）

あわてずにゆっくり考えられますが、そういうノウハウがないままだと

限られた時間の中では、パニックになってしまいますよねー