株価などの危険資産の価格変動は、次のような確率微分方程式で記述されます。
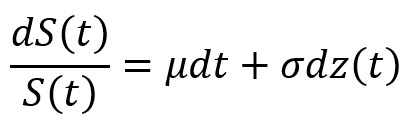
ここで、μはリターン、σはボラティリティ、z(t)は不規則に変動する成分(ノイズ)です。ノイズはブラウン運動に従うもの仮定し、その確率分布は正規分布として扱われます。
今回はこの確率微分方程式の数値解析を試みました。数値積分はエクスプリシット法&モンテカルロ法を採用し、ノイズは乱数で与えることを検討しました。
一般的に乱数を発生させる場合、プログラミング言語で用意される関数を用いると一様分布に従う乱数が生成されます。しかし、今回のノイズは平均0、標準偏差σ(√Δt)の正規分布となるため、一様乱数ではありません。そこで、任意の確率分布に従う乱数を生成させる手法として、「フォン・ノイマンの棄却法」を用いました。
計算結果の一例を掲載します。

【 設定条件 】
資産価格の初期値:S0 = 1000[円]
リターン :μ = 0.1[%/年]
ボラティリティ :σ = 20[%]
時間間隔 :Δt = 1/365[年]
積分期間 :1[年]
※確率過程なので、同じ条件でも計算する度に結果が変わります。

















