算額（その1432）

算額（その1432）

（福島県田村市船引町石森戸屋 稲荷神社 明治18年(1885)）
街角の数学 ～落書き帳「○△□」～ 36．正方形と四分円（2）
http://streetwasan.web.fc2.com/math15.6.17.html
キーワード：四分円2個，正方形3個
#Julia, #SymPy, #算額, #和算

算額（その1431）の拡張で，正方形をもう 1 個加える。
正方形の中に四分円を 2 個を容れ，交差した部分に正方形を 2 個容れる。外側の正方形の一辺の長さが 5 寸のとき，内側の一番小さな正方形の一辺の長さはいかほどか。

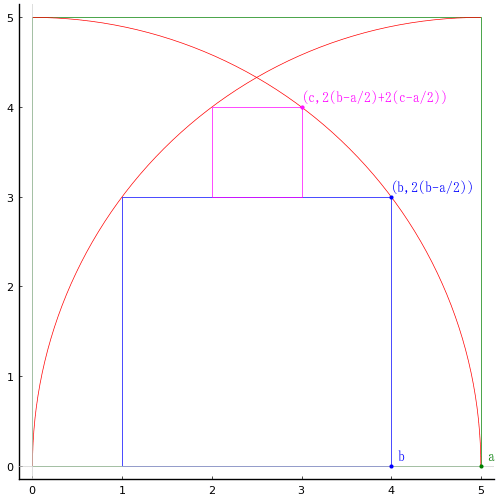
外側の正方形の左下の頂点を原点とし，一辺の長さを a
内側の正方形の右下の頂点の座標を (b, 0)
内側の一番小さな正方形の右下の頂点の座標を (c, 2(b - a/2))
とおき，以下の連立方程式を解く。
内側の 2 つの正方形の右上の頂点いずれもが，原点を中心とする四分円の円周上にあるということを利用する。
内側の正方形の一辺の長さは a - 2(a - b) = 2b - a である。
内側の一番小さい正方形の一辺の長さは a - 2(a - c) = 2c - a である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cfusing SymPy
@syms a::positive, b::positive, c::positive
eq1 = b^2 + (2b - a)^2 - a^2
eq2 = c^2 + ((2b - a) + (2c - a))^2 - a^2
res = solve([eq1, eq2], (b, c))[1]
res |> println

    (4*a/5, 3*a/5)

# b
res[1](a => 5) |> println

    4

# c
res[2](a => 5) |> println

    3

a = 5 のとき b = 4, c = 3 なので，内側の一番小さな正方形の一辺の長さは 2c - a = 1 寸である。

function draw(a, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    b = 4a/5
    c = 3a/5
    plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:green, lw=0.5)
    plot!([a - b, b, b, a - b], [0, 0, 2(b - a/2), 2(b - a/2), 0], color=:blue, lw=0.5)
    plot!([a - c, c, c, a - c], 2(b - a/2) .+ [0, 0, 2(c - a/2), 2(c - a/2), 0], color=:magenta, lw=0.5)
    circle(0, 0, a, beginangle=0, endangle=90)
    circle(a, 0, a, beginangle=90, endangle=180)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(a, 0, " a", :green, :left, :bottom, delta=delta/2)
        point(b, 0, " b", :blue, :left, :bottom, delta=delta/2)
        point(b, 2(b - a/2), "(b,2(b-a/2))", :blue, :left, :bottom, delta=delta/2)
        point(c, 2(b - a/2) + 2(c - a/2), "(c,2(b-a/2)+2(c-a/2))", :magenta, :left, :bottom, delta=delta/2)
    end
end;

draw(5, true)