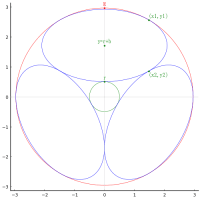
デカルトの正葉線 folium of Descartes を描いてみようと思い,やってみたが自力ではちょっと難しかった。
媒介変数表示だと,大抵は
x = 3*a*t/(1+t^3)
y = 3*a*t^2/(1+t^3)
が紹介されている。しかしこれだと,原点付近が描画できない。
そこで,更に
t = (1+s) / (1-s) と変数変換して,
x = 1.5*a*(1-s)*(1-s^2) / (1+3*s^2)
y = 1.5*a*(1+s)*(1-s^2) / (1+3*s^2)
で描画する。(ということだ)
s = seq(-3.5, 3.5, by=0.01)
x = 1.5*a*(1-s)*(1-s^2) / (1+3*s^2)
y = 1.5*a*(1+s)*(1-s^2) / (1+3*s^2)
plot(x, y, type="l", asp=1)
abline(-a, -1, col=2, lty=2)
abline(0, 1, col=4, lty=2)
abline(v=0, h=0, col=3, lty=3)
極座標系で描くこともできるが,theta の変閾の設定が若干直感的でない気がした。
theta = seq(-0.6, 2.2, by=0.01)
r = 3 * a * sin(theta) * cos(theta) / (sin(theta)^3 + cos(theta)^3)
x = r*cos(theta)
y = r*sin(theta)
plot(x, y, type = "l", asp=1)
abline(-a, -1, col=2, lty=2)
abline(0, 1, col=4, lty=2)
abline(v=0, h=0, col=3, lty=3)