算額（その1431）

算額（その1431）

福島県田村市船引町石森戸屋 稲荷神社 明治18年(1885)
街角の数学 ～落書き帳「○△□」～ 36．正方形と四分円
http://streetwasan.web.fc2.com/math15.6.17.html
キーワード：四分円2個，正方形2個
#Julia, #SymPy, #算額, #和算

正方形の中に四分円を 2 個を容れ，交差した部分に正方形を 1 個容れる。外側の正方形の一辺の長さが 5 寸のとき，内側の正方形の一辺の長さはいかほどか。

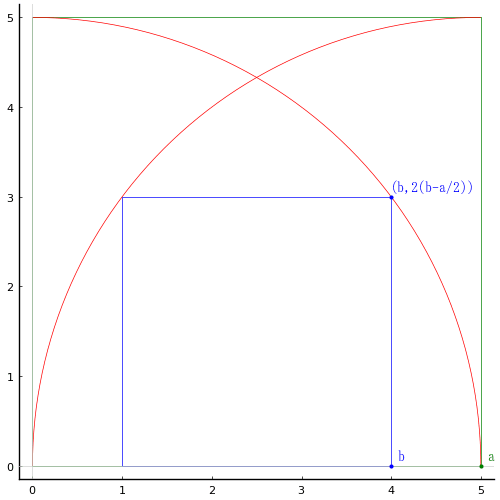
外側の正方形の左下の頂点を原点とし，一辺の長さを a
内側の正方形の右下の頂点の座標を (b, 0)
とおき，以下の連立方程式を解く。
内側の正方形の右上の頂点が原点を中心とする四分円の円周上にあるということを利用する。
内側の正方形の一辺の長さは a - 2(a - b) = 2b - a である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cfusing SymPy
@syms a::positive, b::positive
eq = b^2 + (2b - a)^2 - a^2
res = solve(eq, b)[1]
res |> println
res(a => 5) |> println

    4*a/5
    4

a = 5 のとき b = 4 なので，内側の正方形の一辺の長さは 2b - a = 3 寸である。

function draw(a, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    b = 4a/5
    plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:green, lw=0.5)
    plot!([a - b, b, b, a - b], [0, 0, 2(b - a/2), 2(b - a/2), 0], color=:blue, lw=0.5)
    circle(0, 0, a, beginangle=0, endangle=90)
    circle(a, 0, a, beginangle=90, endangle=180)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(a, 0, " a", :green, :left, :bottom, delta=delta/2)
        point(b, 0, " b", :blue, :left, :bottom, delta=delta/2)
        point(b, 2(b - a/2), "(b,2(b-a/2))", :blue, :left, :bottom, delta=delta/2)
    end
end;

draw(5, true)