最近ゲリラ豪雨という報道用語が用いられることが多い。温暖化に伴って、短時間雨に激しい雨が各地で降っているからであろう。しかしゲリラ豪雨という用語は学術的な用語ではなく、これまでよく用いられてきた集中豪雨という用語と似ている。違うところがあるとすれば、短時間の雨に重点が置かれている点にある。
さて、確率水文量という学術用語について説明しておきたい。確率水文量とは、ある量(例えば1時間雨量)が確率的にどの程度の頻度で起こる量であるかを、再現期間(例えば、10年に1回起こる程度、すなわち1/10程度の確率、10年確率水文量という)で表す水文量である。
これを求める方法は、①通常それぞれの観測点において、観測期間(n年)の年最大1時間雨量を採取する、②それぞれのデータは1/nの等確率で起きていると仮定する、というものである。これらを極値確率紙にプロットし確率曲線(例えばGumbel分布、極値分布A型、B型など)を引く。これを用いてある雨量の超過確率を推定する。その逆数が再現期間を表す。
この説明には厳密でない部分もあるが、手法についてはこれまで確率曲線式にどの式を適用するかの選択についていくつかの提案はあったが、別の手法が提案されたことはない。等確率の仮定や各年最大値が別の年の2位以下の値より小さいことがあるなどの問題が指摘されたが、現在も一般に用いられている方法である。
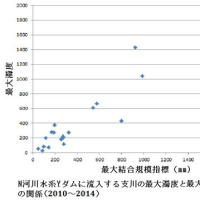
さて、著者が提案している「降水の時間集中度」の正規化の解析結果から導いた図.1を見てほしい。縦軸は1時間雨量、横軸は24時間雨量、図中の曲線は等確率曲線を表している。

この図の特長は、同じ値の1時間雨量の確率評価が24時間雨量によって違うことにある。24時間雨量が多ければ、大きい値の1時間雨量が起こりやすい、低確率で起こるというごく当たり前の結果である。この至極常識的な結果がこれまで見過ごされてきた。常識的と思われてきた年最大1時間雨量が等確率(=1/n)で発生するという仮定は間違っているのである。この事実は、短時間雨量は長時間雨量に従属することがあり、常に独立ではないという点ある。この事実に異論を唱える者はいない。にもかかわらず、年最大1時間雨量発生の等確率(=1/n)の仮定が現在も用いられているのは真に驚きである。
さて、確率水文量という学術用語について説明しておきたい。確率水文量とは、ある量(例えば1時間雨量)が確率的にどの程度の頻度で起こる量であるかを、再現期間(例えば、10年に1回起こる程度、すなわち1/10程度の確率、10年確率水文量という)で表す水文量である。
これを求める方法は、①通常それぞれの観測点において、観測期間(n年)の年最大1時間雨量を採取する、②それぞれのデータは1/nの等確率で起きていると仮定する、というものである。これらを極値確率紙にプロットし確率曲線(例えばGumbel分布、極値分布A型、B型など)を引く。これを用いてある雨量の超過確率を推定する。その逆数が再現期間を表す。
この説明には厳密でない部分もあるが、手法についてはこれまで確率曲線式にどの式を適用するかの選択についていくつかの提案はあったが、別の手法が提案されたことはない。等確率の仮定や各年最大値が別の年の2位以下の値より小さいことがあるなどの問題が指摘されたが、現在も一般に用いられている方法である。
さて、著者が提案している「降水の時間集中度」の正規化の解析結果から導いた図.1を見てほしい。縦軸は1時間雨量、横軸は24時間雨量、図中の曲線は等確率曲線を表している。

この図の特長は、同じ値の1時間雨量の確率評価が24時間雨量によって違うことにある。24時間雨量が多ければ、大きい値の1時間雨量が起こりやすい、低確率で起こるというごく当たり前の結果である。この至極常識的な結果がこれまで見過ごされてきた。常識的と思われてきた年最大1時間雨量が等確率(=1/n)で発生するという仮定は間違っているのである。この事実は、短時間雨量は長時間雨量に従属することがあり、常に独立ではないという点ある。この事実に異論を唱える者はいない。にもかかわらず、年最大1時間雨量発生の等確率(=1/n)の仮定が現在も用いられているのは真に驚きである。
















※コメント投稿者のブログIDはブログ作成者のみに通知されます