初手から☗7六歩☖3四歩☗2六歩☖3二金(第1図)。後手の一手損角換り戦法の出だしです。最近だと棋聖戦第二局の佐藤棋聖,王位戦第二局の羽生王位,竜王戦挑戦者決定トーナメントの中原永世十段が採用しています。

ここで先手は☗7八金☖8四歩☗2五歩(第2図)か単に☗2五歩(第3図)。棋聖戦の渡辺竜王と王位戦の深浦八段は前者,竜王戦の谷川九段は後者でした。どちらを選ぶかは好みでしょうが,☖8四歩とすれば後手が飛車を振る可能性はかなり低くなります。それを先手の得とみれば☗7八金を選んだ方がいいでしょうし,そうでもないと考えるなら単に☗2五歩でも問題ないと思います。

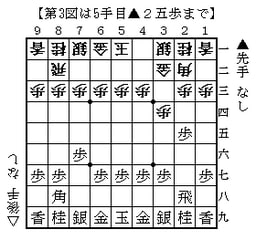
先手が☗2五歩と突いたのをみて☖8八角成とするのがこの戦法の骨子。以下☗同銀☖2二銀(第4図か第5図)と進みます。


これとは別の手順があります。☗7六歩☖3四歩☗2六歩に☖9四歩(第6図)。この戦法を採用することが多い丸山九段は,最近はこの手順が多いようで,先日の銀河戦Bブロック11回戦でもこう指しました(棋譜は囲碁・将棋チャンネルホームページ。左の番組紹介→銀河戦→Bブロック)。
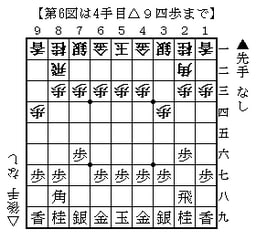
この場合,先手は☗7八金とは上がれません。☖4四歩から振飛車にすれば後手が一本取った形になります。また☗9六歩と受けた場合も,先手が居飛車穴熊に組みにくい意味があるので,後手は振飛車にするのが有力と思えます。
したがって☖9四歩には銀河戦の木村八段のように☗2五歩とするのが普通。そこで☖8八角成☗同銀☖2二銀(第7図)。
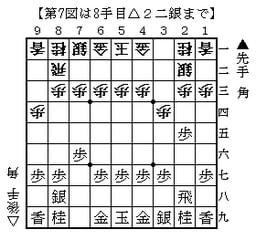
この場合の後手もどちらを選ぶかは好みの問題かもしれません。丸山流は,先手の模様をみて居飛車にも振飛車にもでき,その分だけ先手の駒組を牽制できますが,一手損の上に端歩を突くので,立ち遅れるリスクを伴います。
どちらの指し方をしても同様に一手損角換りといわれます。しかしこれだけ異なった手順が同じ名前で呼ばれているのは,いささか不思議な気もします。
明日は福井記念の決勝。並びは伏見ー手島ー坂本の東日本,永井ー富永ー前田の中部近畿,渡部ー友定の四国中国で,山口は富永と競るようです。僕は永井選手に期待します。
これは僕にとっては少しばかり意外なことなのですが,『エチカ』においては無限を意味するinfinitumよりも,有限を意味するfinitumの方が先に出てきます。そこでここでもスピノザが選んだその順序に倣って,まず事物が有限であるということが具体的にはどのようなことであるのかということを考えていくことにします。これは第一部定義二で,この定義Definitioは純粋に定義であるといい得るような最初の一文と,それについての説明から成っていると,僕は考えています。長くなりますがここではその全文を示すことにします。
「同じ本性の他のものによって限定されうるものは自己の類において有限であると言われる(Ea res dicitur in suo genere finita, quae)。例えばある物体は,我々が常により大なる他の物体を考えるがゆえに,有限であると言われる。同様にある思想は他の思想によって限定される。これに反して物体が思想によって限定されたり思想が物体によって限定されたりすることはない」。
最初の一文が,事物が有限であるということについての純粋な定義であるとすれば,僕の考えでは,その説明にあたる残りの部分は,定義というよりは,ある公理的性格を帯びていると思います。その根拠となるのは,以前にテーマとして採用した第一部公理五であるということになると思うのですが,いきなり本来のテーマとあまり関係しないようなことを考えるのも変ですので,ここではこの問題については触れずに,先に進んでいくこととします。

ここで先手は☗7八金☖8四歩☗2五歩(第2図)か単に☗2五歩(第3図)。棋聖戦の渡辺竜王と王位戦の深浦八段は前者,竜王戦の谷川九段は後者でした。どちらを選ぶかは好みでしょうが,☖8四歩とすれば後手が飛車を振る可能性はかなり低くなります。それを先手の得とみれば☗7八金を選んだ方がいいでしょうし,そうでもないと考えるなら単に☗2五歩でも問題ないと思います。


先手が☗2五歩と突いたのをみて☖8八角成とするのがこの戦法の骨子。以下☗同銀☖2二銀(第4図か第5図)と進みます。


これとは別の手順があります。☗7六歩☖3四歩☗2六歩に☖9四歩(第6図)。この戦法を採用することが多い丸山九段は,最近はこの手順が多いようで,先日の銀河戦Bブロック11回戦でもこう指しました(棋譜は囲碁・将棋チャンネルホームページ。左の番組紹介→銀河戦→Bブロック)。

この場合,先手は☗7八金とは上がれません。☖4四歩から振飛車にすれば後手が一本取った形になります。また☗9六歩と受けた場合も,先手が居飛車穴熊に組みにくい意味があるので,後手は振飛車にするのが有力と思えます。
したがって☖9四歩には銀河戦の木村八段のように☗2五歩とするのが普通。そこで☖8八角成☗同銀☖2二銀(第7図)。

この場合の後手もどちらを選ぶかは好みの問題かもしれません。丸山流は,先手の模様をみて居飛車にも振飛車にもでき,その分だけ先手の駒組を牽制できますが,一手損の上に端歩を突くので,立ち遅れるリスクを伴います。
どちらの指し方をしても同様に一手損角換りといわれます。しかしこれだけ異なった手順が同じ名前で呼ばれているのは,いささか不思議な気もします。
明日は福井記念の決勝。並びは伏見ー手島ー坂本の東日本,永井ー富永ー前田の中部近畿,渡部ー友定の四国中国で,山口は富永と競るようです。僕は永井選手に期待します。
これは僕にとっては少しばかり意外なことなのですが,『エチカ』においては無限を意味するinfinitumよりも,有限を意味するfinitumの方が先に出てきます。そこでここでもスピノザが選んだその順序に倣って,まず事物が有限であるということが具体的にはどのようなことであるのかということを考えていくことにします。これは第一部定義二で,この定義Definitioは純粋に定義であるといい得るような最初の一文と,それについての説明から成っていると,僕は考えています。長くなりますがここではその全文を示すことにします。
「同じ本性の他のものによって限定されうるものは自己の類において有限であると言われる(Ea res dicitur in suo genere finita, quae)。例えばある物体は,我々が常により大なる他の物体を考えるがゆえに,有限であると言われる。同様にある思想は他の思想によって限定される。これに反して物体が思想によって限定されたり思想が物体によって限定されたりすることはない」。
最初の一文が,事物が有限であるということについての純粋な定義であるとすれば,僕の考えでは,その説明にあたる残りの部分は,定義というよりは,ある公理的性格を帯びていると思います。その根拠となるのは,以前にテーマとして採用した第一部公理五であるということになると思うのですが,いきなり本来のテーマとあまり関係しないようなことを考えるのも変ですので,ここではこの問題については触れずに,先に進んでいくこととします。














