⑰-4から先手は⑰-5で示した手順に進めるべきだったのですが,考えた末にそれを逃しました。実際に指された手は☗9四桂です。
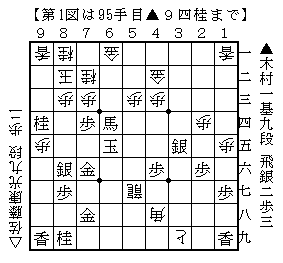
僕はAbemaの中継を視聴していましたから,先手の考慮中にどう指すのかを考えていました。しかしこの手は僕にはまったく思いついていない手でした。
実際にはこの手は悪手で,第1図を境にして後手が優勢になっています。現在のようにAIの評価値が出るのであれば僕にもそのことが即座に分かったでしょう。ですが当時はそれがありませんでしたから,この時点ではそのことが分かりませんでした。というよりこの手を見たときには,先手の勝ちになったのだろうと勘違いしたのです。それは次のような事情からです。
先手がそれなりに時間を使った末に,僕には思いついていない手が指されました。プロがそれだけ考えて僕には思い浮かばないような手を指したときには,勝ちを見つけたということだろうと想定するのです。とくに実際に指された手というのは,桂馬をただで捨ててしまう手だったので,なおのことこのときはそう思ったのです。
たぶんこの後だったと思いますが,先手が席を外したとき,考慮中の後手から「えー」という小さな声が上がりました。僕はその声の意味を,当時は後手も読んでいなかった手を指されたためだと思ったのですが,今から考えれば,これは自分が急に勝ちになったための驚きだったのかもしれません。
柏葉が指摘していること,すなわち,円の中には無限に多くのinfinita長方形があるけれど,それらすべての長方形が現実的に存在することは不可能であるということは,論理的には正当化することができます。
円の中には無限に多くの長方形があるのですが,このとき,たとえばAとBという長方形が現実的に存在すると仮定してみます。このとき,長方形Aと長方形Bの区別distinguereは様態的区別です。したがってこれらの長方形は数によって区別することが可能です。いい換えれば,この場合は円の中にふたつの長方形だけが現実的に存在しているということができます。ところでこのことは,円の中にある長方形が現実的に存在する場合には必ず妥当しなければなりません。つまりAとBのほかにCという長方形が現実的に存在するのであれば,CもまたAおよびBとは様態的に区別されるのですから,みっつの長方形があることになるのです。このようにして数をどんどん加えていって,最終的にすべての長方形が現実的に存在すると仮定するなら,それらの長方形は数によって示すことができるということになるでしょう。しかし,もしあるものの数を示すことができるのであるとすれば,そうしたものは有限finitumといわれなければなりません。したがってこの場合は有限個の長方形が円の中にあるといわなければならず,円の中に無限に多くの長方形があるという仮定に反します。いい換えれば,円の中に無限に多くの長方形があるということは,たとえばどんなに無際限に円の中の長方形が現実的に存在したとしても,他面からいえば,円の中にいくら無際限に多くの長方形を描いていったとしても,すべての長方形が現実的に存在するようになること,あるいはそれを描き切るということは不可能なのであって,さらにほかの長方形が現実的に存在し得るし,またほかの長方形を描くことができるという意味でなけれならないのです。
よって,柏葉の指摘が論理的に正しいということを僕は認めます。ただし,第二部定理八備考を読解するときに,この論理が有益であるかどうかということについては,僕は確信をもって同意することはできません。この比喩の意図は不明であるからです。

僕はAbemaの中継を視聴していましたから,先手の考慮中にどう指すのかを考えていました。しかしこの手は僕にはまったく思いついていない手でした。
実際にはこの手は悪手で,第1図を境にして後手が優勢になっています。現在のようにAIの評価値が出るのであれば僕にもそのことが即座に分かったでしょう。ですが当時はそれがありませんでしたから,この時点ではそのことが分かりませんでした。というよりこの手を見たときには,先手の勝ちになったのだろうと勘違いしたのです。それは次のような事情からです。
先手がそれなりに時間を使った末に,僕には思いついていない手が指されました。プロがそれだけ考えて僕には思い浮かばないような手を指したときには,勝ちを見つけたということだろうと想定するのです。とくに実際に指された手というのは,桂馬をただで捨ててしまう手だったので,なおのことこのときはそう思ったのです。
たぶんこの後だったと思いますが,先手が席を外したとき,考慮中の後手から「えー」という小さな声が上がりました。僕はその声の意味を,当時は後手も読んでいなかった手を指されたためだと思ったのですが,今から考えれば,これは自分が急に勝ちになったための驚きだったのかもしれません。
柏葉が指摘していること,すなわち,円の中には無限に多くのinfinita長方形があるけれど,それらすべての長方形が現実的に存在することは不可能であるということは,論理的には正当化することができます。
円の中には無限に多くの長方形があるのですが,このとき,たとえばAとBという長方形が現実的に存在すると仮定してみます。このとき,長方形Aと長方形Bの区別distinguereは様態的区別です。したがってこれらの長方形は数によって区別することが可能です。いい換えれば,この場合は円の中にふたつの長方形だけが現実的に存在しているということができます。ところでこのことは,円の中にある長方形が現実的に存在する場合には必ず妥当しなければなりません。つまりAとBのほかにCという長方形が現実的に存在するのであれば,CもまたAおよびBとは様態的に区別されるのですから,みっつの長方形があることになるのです。このようにして数をどんどん加えていって,最終的にすべての長方形が現実的に存在すると仮定するなら,それらの長方形は数によって示すことができるということになるでしょう。しかし,もしあるものの数を示すことができるのであるとすれば,そうしたものは有限finitumといわれなければなりません。したがってこの場合は有限個の長方形が円の中にあるといわなければならず,円の中に無限に多くの長方形があるという仮定に反します。いい換えれば,円の中に無限に多くの長方形があるということは,たとえばどんなに無際限に円の中の長方形が現実的に存在したとしても,他面からいえば,円の中にいくら無際限に多くの長方形を描いていったとしても,すべての長方形が現実的に存在するようになること,あるいはそれを描き切るということは不可能なのであって,さらにほかの長方形が現実的に存在し得るし,またほかの長方形を描くことができるという意味でなけれならないのです。
よって,柏葉の指摘が論理的に正しいということを僕は認めます。ただし,第二部定理八備考を読解するときに,この論理が有益であるかどうかということについては,僕は確信をもって同意することはできません。この比喩の意図は不明であるからです。
























※コメント投稿者のブログIDはブログ作成者のみに通知されます