リアルインパクト＆数学の内実

　日曜のNHKマイルカップを勝ったラウダシオンの父はリアルインパクトです。父はディープインパクト。母はトキオリアリティー。6つ上の半兄に2007年にオーシャンステークスを勝ったアイルラヴァゲイン。3つ下の半弟に2016年に札幌記念,2017年に中山記念とクイーンエリザベスⅡ世カップを勝ったネオリアリズム。
　2歳10月にデビュー。新馬を勝つとすぐに京王杯2歳ステークスに挑戦して2着。朝日杯フューチュリティステークスも2着でした。
　3歳初戦のニュージーランドトロフィーは11着。一叩きして挑んだNHKマイルカップで3着になると,古馬相手の安田記念に進み,大レース制覇を達成しました。安田記念は第1回と2回を3歳馬が勝っているのですが,それ以外に3歳で勝ったのはこの馬だけです。
　秋は毎日王冠で復帰して2着。マイルチャンピオンシップは1番人気に支持されるも5着。阪神カップも1番人気で10着でした。
　4歳の初戦は中山記念で3着。マイラーズカップは最下位。安田記念が6着でした。
　4歳秋は毎日王冠を4着。マイルチャンピオンシップが5着でした。
　5歳初戦の東京新聞杯は11着。中山記念が8着でダービー卿チャレンジトロフィーは12着でした。
　立て直して挑んだ富士ステークスで2着。マイルチャンピオンシップは10着でしたが阪神カップを制覇。1年半ぶりの勝利をあげました。
　6歳春はスプリント路線に参戦。オーシャンステークスが8着,高松宮記念が9着。マイルに戻った安田記念も13着でした。
　秋は11月のオープンで復帰。これは6着でしたが,阪神カップで連覇を達成しました。
　7歳春はオーストラリアに遠征。ジョージライダーステークスを制覇しドンカスターマイルで2着と,大きな戦果をあげました。帰国して出走した安田記念は12着。
　ラストシーズンとなった7歳秋は毎日王冠が12着でマイルチャンピオンシップが8着でした。
　日本でひとつ,オーストラリアでひとつの大レースを勝った馬ですが,一流馬といえるほどの成績を残せたわけではありません。その中から大レースの勝ち馬が出たのですから,種牡馬としては大成功といっていいくらいだと思います。

　僕がこの考察では,数学は存在論であるとするバディウAlain Badiouのテーゼの立場は採用しないということ,ならびになぜその立場を採用しないかという理由は概ね理解してもらえたものと思います。また同時に,スピノザがカントールGeorg Ferdinand Ludwig Philipp Cantorの数学を知らなかったことも前提とした上で,スピノザにとって数学という語が示す内実がどういったものであったかを考察していくということにも留意しておいてください。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　『主体の論理・概念の倫理』の三者鼎談の中で,スピノザにとって数学とは幾何学的方法であったと発言しているのは上野です。そしてそのことに上野は,経験には頼らずに対象を創出していく学問であるという主旨の説明をしています。つまりスピノザは個別の計算とか解析といったものについてはそれを重視しないといっていることになります。
　僕はこのこと自体は正しいと思います。ただこのことは数学に限られたことではないとも思うのです。というのは,オルデンブルクとの文通が事実上はロバート・ボイルRobert Boyleとの化学に関わる論争に入ったとき,スピノザはボイルの実証的な実験についてはそれをさほど重視しておらず,むしろ実験の結果effectusを原因causaから結果の方へと辿ることについて意欲を示しているからです。ボイルの方は実験の方を重視していましたから,実験の結果についての部分を別にすれば,ふたりの論争はその点が中心となっています。
　しかし,僕はだからスピノザがボイルの実験を化学であると認めていないというようには思いません。これは幾何学的方法をスピノザが重視していたとはいえ,スピノザ自身もまた様ざまな実験を行っていたという事実がそれを証明しているといっていいのではないかと思います。そしてそれと同じように,スピノザは経験には訴えない数学というものを重視していたのですが,だからといって個別の計算とか解析について,それを数学とは認めていなかったとは思いません。上野のいい方だと,スピノザは幾何学的方法だけを数学と認識していたことになるので,個別の計算や解析は数学として認めなかったということになるのですが,僕はそのような解釈は採用しませんし,上野の説明にも別の意図があったと思います。

入手の困難性＆存在論と数学

　僕が規定した羨望という感情affectusは,羨望を抱く相手に対する同類意識が高まれば高まるほど,その感情を抱きやすくなり,また抱いた感情が大きくなりやすいということが分かりました。そしてこれとは別に,ほかの条件が一致するなら,この羨望という感情を大きくしやすい別の要素があります。
　羨望という感情は,ある人間が入手していない喜びlaetitiaという感情を,他者が入手して喜んでいる場合に,感情の模倣imitatio affectuumを介してその喜びを入手することに向う欲望cupiditasでした。このとき,その喜びを自分も入手するということについては,一律に規定することはできません。どんな人間にとっても,それをいまだに手にしていないとき,それを入手することについては,容易であると表象される場合もあれば,困難であると表象するimaginari場合もあるからです。現実的にいっても,僕たちには得やすい喜びと得難い喜びがあるということは,僕たちは経験的に知っている筈ですから,このこと自体はこれ以上の説明は要さないでしょう。この場合に,それが自分にとって得難い喜びであると表象されるときの方が,それは得やすい喜びであると表象されるときよりも,それを手にした人に対する羨望は,ほかの条件が同一であるなら大きくなるのです。
　あることの困難さとか容易さというのは,実際にはそのことそのものの本性essentiaや特質proprietasであるというわけではなく,僕たちの認識cognitioに完全に依存します。しかし僕たちが実際にある事柄については容易であると認識し,別の事柄については困難であると認識するcognoscereことは,一般的に同様に,つまり万人が同様に認識するわけではありませんが,諸個人がそのような認識を有するということはあるのです。よってこのことによって羨望の大きさが左右されるということもしばしば生じるのです。
　ここからさらに別のことも分かります。Ａがある喜びを入手し,ＢとＣはそれを入手していないとしましょう。このとき,その喜びを入手することをＢは困難と表象し,Ｃは容易と表象するなら,実際に上述の前提からこのような事象は生じ得るわけですが,この場合は他の条件が同じなら,Ｂの方がＣよりも大きな羨望をＡに対して感じるのです。
　入手の困難性の認識は,羨望という感情の度合に対して,同類意識の高さと同じように,強い影響を与えます。

　メイヤスーQuentin MeillassouxがいうにはバディウAlain Badiouは数学は存在論であるというテーゼを立てていました。このテーゼは,近藤がバディウの主張を要約するときにも原点となっているものです。したがってバディウは確かに数学は存在論であると考えていたのでしょう。このゆえに,バディウの立場からしてみれば,数学と存在論は切り離せないものです。よって,もしバディウが,自分の主張する存在論と,スピノザの存在論との間に齟齬があるあるいは対立があると判断するなら,バディウはその齟齬ないしは対立を,単なる存在論的な齟齬であり対立であると解するのではなく,数学的な対立でもあると解することになるでしょう。そして実際にバディウの主張とスピノザの主張との間には,前者が多の存在論であり後者は一の存在論であるという対立があり,またそのゆえに前者には空があるけれど後者には空はないという齟齬つまり対立があるのですから,バディウが自身とスピノザとの間には数学的な対立があると解したとしても,たとえスピノザはカントールGeorg Ferdinand Ludwig Philipp Cantorの数学つまり集合論を知らなかったという事情を考慮するにせよ,間違ってはいなかったと思います。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　僕がここでいうのは,しかし僕はここではそのようなバディウの立場には立たないということです。あるいは同じことですが,僕は数学は存在論であるというテーゼは立てないということです。スピノザは方法として幾何学的方法が優れていると考えていたことは間違いありません。そしてそれを最良の数学的方法であると認識していたのも間違いありません。これらのことは『主体の論理・概念の倫理』の考察でも参照した,『デカルトの哲学原理Renati des Cartes principiorum philosophiae pars Ⅰ,et Ⅱ, more geometrico demonstratae』におけるマイエルLodewijk Meyerによる序文から明白だといえます。しかしだからといってスピノザは存在論も数学であると考えているわけではなく,存在論を解明する方法として最善の方法は数学的方法であるといっているのだと僕は解します。いい換えれば数学が幾何学的方法によって解明されるのと同じように,存在論ももしそれが解明されるのであれば,幾何学的方法によって解明されるべきなのだし,幾何学的方法によって最も理解が容易なふうに解明することが可能であるといっているのだと解します。

東京スポーツ賞川崎マイラーズ＆空と学知

　昨晩の第12回川崎マイラーズ。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　逃げ候補の1頭だったワークアンドラブは,発走後の周回コースとの合流点で内に逃避してしまいました。これもありサルサディオーネが逃げることに成功。カジノフォンテンが2番手でマーク。3番手のキャプテンキングまでは差がなく続きました。2馬身差でリッカルド。2馬身差でグレンツェント。2馬身差でアンサンブルライフとウェイトアンドシー。2馬身差でバンドオンザランとクリスタルシルバー。3馬身差でクインズサターン。ワークアンドラブとジャーニーマンとトーセンガーネットが後方を追走という縦長の隊列。前半の800mは48秒6のハイペース。
　3コーナーを回るとカジノフォンテンがサルサディオーネに並び掛けていきました。サルサディオーネはコーナーの中間では早くも鞭が入って苦しくなりました。カジノフォンテンの外に並んできたのがリッカルドで,直線に入るとまずこの2頭の争い。リッカルドがカジノフォンテンを競り落として先頭に立つと,直線の入口ではこれらの直後まで追い上げていたグレンツェントが伸びてきて,リッカルドを楽に差し切って優勝。リッカルドが2馬身半差で2着。内にいたため直線で外に切り返すロスが生じたキャプテンキングが半馬身差の3着。
　優勝したグレンツェントは南関東重賞初勝利。昨年の8月まではJRAで走っていた馬で,レパードステークス,東海ステークスと重賞2勝。このクラスの馬は多少は頭打ちになっても南関東重賞なら通用するレベルで,実際に転入初戦は2着でした。ところがその後の3戦は思ったほど走ることができなかったため,僕もここは評価を下げていました。このレースはここ3戦よりはいい位置でレースを進めていましたので,そのあたりが勝因になったといえそうです。ですからこれからも結果は位置取り次第ということになるのではないでしょうか。父はネオユニヴァース。Glanzendはドイツ語で輝く。
　騎乗した船橋の森泰斗騎手は金盃以来の南関東重賞36勝目。川崎マイラーズは初勝利。管理している大井の藤田輝信調教師は南関東重賞16勝目。川崎マイラーズは初勝利。

　ここからの考察で僕が集合論について言及する場合は,それが概念notioとして空を必要とする数学であるという点を念頭に置いていることに注意しておいてください。僕は数学としての集合論には詳しくありませんから,スピノザの哲学から集合論をみるという場合には,この点にしか注目することができないのです。バディウAlain Badiouはスピノザの存在論には空がないということでそれを批判したのですが,空があるような理論をスピノザが数学として,もっと広くいえばひとつの学知scientiaとして認めることがあるかどうかを検討することは,意味がないことであるとは思いません。
　次に,バディウが集合論といっているのは,カントールGeorg Ferdinand Ludwig Philipp Cantorの数学のことでした。カントールは1800年代の後半から1900年代の前半にかけて活躍した数学者です。したがってこれは当然のことですが,1600年代を生きたスピノザはカントールを知りません。要するにスピノザは集合論を知らないわけです。ですから,スピノザが集合論をひとつの学知として認め得るのかということは,ある意味では仮定としての課題です。よって,集合論そのものについて考えるよりも,空を概念として必要とする理論というように,それを一般化した方が,適切な解答を出せるという一面があります。つまり僕はここでは数学,集合論を含めた数学について探求していくわけですが,その中で集合論について言及する場合には,数学的な観点よりは空,いい換えれば存在論的観点を重視することになります。なので,その場合に集合論について妥当する事柄は,もっと一般的に,存在論的観点からみればスピノザが認めないであろう空を概念とする学問一般についても妥当することになるでしょう。
　一方,スピノザがカントールを知らなかった,集合論を知らなかったということは,バディウも承知の上だった筈です。バディウがスピノザの哲学を批判するとき,そのことを忘れていたという可能性はさすがにないだろうと僕は思います。その上でバディウは,スピノザの哲学には空がないといって批判するのですから,事実上はその批判は数学的な批判というよりも,存在論的な批判であったといっていいと僕は思います。

マイナビ女子オープン＆数学の範囲

　昨日の第13期マイナビ女子オープン五番勝負第三局。
　加藤桃子女流三段の先手で西山朋佳女王のノーマル三間飛車の将棋。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　第1図で相場は☗７八玉です。ですが☗４六歩と突きました。居飛車は5筋の歩を突くパターンが多いので珍しい手だと思います。
　後手が☖６二王と上がったところでいきなり☗４五歩。☖同歩☗３三角成☖同銀と交換して,交換した角を☗６五角と打ちました。後手が☖７四歩と角成の方を受けると☗３二角成☖同金の飛車角交換に持ち込んで,取った飛車を☗４一飛と打ちました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　攻めが成立しているかどうかは正直なところ微妙だと思います。ただこれは先手が研究して進めた手順に違いなく,後手はその場で対応していかなければならないので,その分だけ後手にとっては大変でした。この乱戦を避けようとするなら,もし第1図でこの将棋のように☗４六歩と突いてきたら,☖４三銀と備えておくのがよさそうです。
　加藤三段が勝って2勝1敗。第四局は18日に指される予定です。

　『主体の論理・概念の倫理』の考察の中の,バディウAlain Badiouに関連する補足はこれですべてです。簡潔にまとめれば,バディウとスピノザの間にあった対立というのは,集合論と公理論の間にある数学的な対立ではなく,多の存在論と一の存在論の間の哲学的な対立であったことになります。バディウはその存在論のことを数学というのですから,確かにバディウからしてみれば,これは哲学的な対立ではなく数学的な対立だったというのが正しいかもしれません。ですがこのブログはスピノザの哲学を扱うブログなのであって,その立場からいえば,そこには哲学的な対立があったと解しておくのが分かりやすいですし,また適切でもあると僕は考えます。
　バディウの主張に関する補足はこれだけなのですが,僕としてはこのことと関連して別の考察をしておきたいので,それについてこれから述べていきます。ただ注意しておいてほしいのは,この部分は僕自身の考察なのであって,この考察の契機となっている『〈内在の哲学〉へ』とは無関係であるということです。
　『主体の論理・概念の倫理』の考察においては,スピノザは幾何学的方法が数学であると考えていたということを,上野の発言に基づいて考察の前提としていました。スピノザは数学というのを有益な学問である,人間が真理veritasの何たるかを知るために大いに役立つ学問であるという認識cognitioをもっていました。このことは間違いないと僕は思います。ただそのときにスピノザが数学ということで示していたのは,幾何学的方法を用いた公理論のことであり,僕たちが広く数学という語の意味に含ませようとするすべての事柄が含まれていたわけではない可能性があったので,そういう前提は必要であったのです。そこでここからは,幾何学的方法とは無関係,あるいは異なった方法を用いる数学,というのは広い意味での数学ということになりますが,それをスピノザが数学であると認めるのかどうかということを検討しておきたいのです。というのは,これを検討することによって,たとえば集合論の論理構成について,それを数学であるとスピノザは認めるのかということまで結論が出せるのではないかと思うからです。

印象的な将棋⑯－７＆空の不在

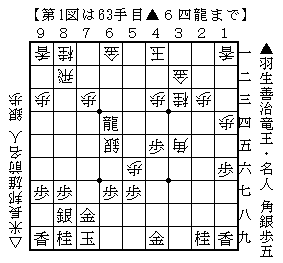
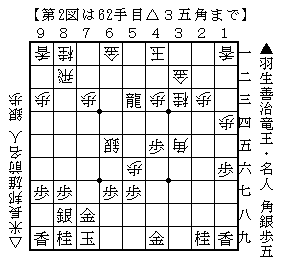
　⑯－６の第2図は龍取りですから,先手は龍を逃げなければなりません。逃げ場所は3つありますが,☗５五龍は☖５七歩成が厳しく後手の勝勢。☗６三龍は☖６二飛で先手の龍と後手の飛車の交換が避けられないので先手の損。なので☗６四龍とするほかありません。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　この手は金銀の両取りになっています。６五の銀はともかくこのまま王手で６一の金を取られてはいけません。なので☖６二飛として銀取りを受けるのは当然でしょう。
　この将棋は⑯－３でいったように,先手から誘導したものです。ただ後手の対応の仕方により,先手としてはあまり変化する余地がないままここまで進みました。そしてここにきて,先手にはふたつの有力な変化がある局面に至りました。ひとつは☗６三銀と飛車取りに打って６五の銀を取りにいく順で,もうひとつが☗６三角と王手をして６五の銀を取りにいく順です。実戦は☗６三銀と打ちましたが,先手が一手負けの順に進みましたので,ここでは☗６三角の方がよかった可能性はあります。
　☗６三銀は王手ではありませんので後手は☖５七歩成と指しました。ここでは飛車は取れませんので先手は☗７七銀と玉の逃げ道を作ります。そうしておいて後手は☖８二飛と逃げました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　何もせずに飛車を逃げたのが好手で,ここからは後手の勝ち筋に入っているようです。

　分割することができない絶対的な量から,個々の分割することが可能な有限finitumの量が発生することを示しているのが第一部定理一六です。もちろん,量として規定されるのは延長の属性Extensionis attributumに属するものだけです。属性は無限に多くあり,この定理Propositioはそれらの属性についても同じことをいっています。ただ,どういう場合であっても,絶対的なもの,無限なものから有限であるものが発生するとこの定理はいっているのであり,延長の属性に属する量はそのひとつです。
　これがスピノザの実在論の原理であると,上野はいっているのです。上野はそれを,あるものすべてという存在existentiaのドメインを確定してしまう方法だと述べています。もっともこの点は,実在論の可能性について言及している部分なので,ここでは詳しい説明を省きます。現在の考察との関連で僕が重視したいのは,スピノザは上野がいうあるものすべてというのを,神Deusのうちにあるものとして規定していることです。それが第一部定理一五です。そして何より注意したいのは,あるものすべてが神のうちにあり,なおかつ神なしには何もあることができないとするなら,端的にあるものだけがすべてで,それ以外に何かがあるという余地はないということです。
　バディウAlain Badiouは,存在論が多の存在論であるなら,多は空でなければならないといっていました。ところがスピノザの実在論では空があるという余地はありません。このことがバディウにとっては大きな問題点でしたし,また近藤が,バディウにとっての唯一の理論的なライバルがスピノザの『エチカ』であるといったことの意味であったと思われます。したがって,もしもこの観点からバディウがスピノザの公理論を理解することができなかったという,『主体の論理・概念の倫理』における近藤の発言を解するなら,バディウが理解できなかった,あるいは同意することができなかったのは,公理論そのものではなかったのはもちろん,幾何学的方法そのものでもなく,第一部定理一五であったと解するのが適当であると僕は考えます。幾何学的方法を採用すると,必ず第一部定理一五に示される事柄が導き出されなければならないとは,僕には考えにくいからです。

ロッシー・小川＆実在論の可能性

　クラッシュギャルズをプロデュースしていたのは,長与千種とフロントのロッシー・小川であったとライオネス・飛鳥は語っています。小川はプロレスラーではない人物の中ではひとりだけ,『1993年の女子プロレス』のインタビューを受けています。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　小川は1978年に全日本女子プロレスに入社していますので,ビューティペアの時代から全日本女子プロレスのフロントの一員でした。そしてビューティペア以前と以後では大きな変化があったといっています。プロレスそのものに変化があったわけではないけれど,主流が日本人対決になった点がそれです。男子のプロレスで日本人対決が主流になったのは,長州力が維新軍を結成してからです。もちろんそれまでも日本人対決はありましたが,それは散発的なものであり,主流とはいえません。日本人対決を主流としたという点では,全日本女子プロレスは日本のプロレス業界全体を先取りしていたといえるのかもしれません。
　小川が全日本女子プロレスで最も仕事を任されたのは,対抗戦の時代だったそうです。『1993年の女子プロレス』とは,女子プロレスが対抗戦で最も盛り上がった時代のことを意味します。その時代は全日本女子プロレスのマッチメークのほとんどは小川が決めていたということですから,その盛り上がりに一役買っていたことは間違いありませんし,小川が存在していなければあの盛り上がりはなかったのかもしれません。
　この対抗戦の時代に,他団体で評価していた選手として3人の名前をあげています。LLPWのイーグル・沢井と紅夜叉,そしてJWPの福岡晶です。ただし福岡は原石として評価していたといっていますので、将来のスターとして評価したという意味だと思われます。沢井とか紅夜叉というのは,失礼ないい方かもしれませんが,団体のトップになるというタイプの選手というよりは,脇役としていい仕事をするタイプの選手であったように僕には思えます。それだけに小川がこのふたりを評価しているのは意外でした。

　『主体の論理・概念の倫理』の三者鼎談の中で,上野修から以下のような発言がありました。ただしこれはバディウAlain Badiouに対する言及とは無関係の箇所で,実在論の可能性について議論している箇所です。
　スピノザは第一部定理一三系において,物体的実体substantia corporeaは分割され得ないということを主張しています。ここではこの考察を分かりやすくするため,スピノザは分割することができない量というものが存在すると主張したと解しておきます。物体は何らかの量によって規定することが可能な筈ですから,こうした解釈は誤っているということにはならないでしょう。いい換えればスピノザは,量というものを絶対的なものとしてみていたということになります。僕たちは量というのを知覚するpercipere場合には,必ず有限なfinitumものとして知覚することになるので,これは上野のことばを借りていえば,スピノザは量を形而上学的なものとして把握していたということになります。スピノザが数学ということで相手にしようとしているのは,このような意味での量であると考えても差し支えありません。
　このように量を把握することは,実在論としてある特殊な意味を有することになります。もし何かあるものが実在しているということを主張しようとするならば,それをカテゴライズするために何らかの一般的概念あるいは普遍的概念notiones universalesが必要とされます。たとえば人間が実在すると主張するならば人間という普遍概念が必要ですし,馬が実在するといいたいのであれば馬という一般的概念が必要とされるのですから,このことはそれ自体で明白であるといっていいでしょう。ところがスピノザは,初めに形而上学的な絶対的な量というのを規定することによって,そうした普遍的概念あるいは一般的概念を必要とせずに,実在論を展開することができます。いい換えれば人間であろうと馬であろうと,もちろんほかに実在するどんなものであろうと,絶対的な量を直接的な原因causaとする因果論によって,個別に量化してしまうのです。たとえば運動motusと静止quiesの割合ratioとしてスピノザがある個別の物体を示そうとするとき,そこで実際に行われているのはそのような作業であると解釈することができるでしょう。

NHKマイルカップ＆不同意の理由

　第25回NHKマイルカップ。
　シャチは発馬のタイミングが合わず1馬身の不利。レシステンシアがすぐに先頭に立ち,ラウダシオンが2番手でマーク。3番手はタイセイビジョン,プリンスリターン,ギルデッドミラー,ストーンリッジの集団。2馬身差でボンオムトゥック。8番手にシャインガーネットとメイショウチタン。10番手にラインベック。11番手にハーモニーマゼラン。12番手はシャチ,サクセッション,ソウルトレインの3頭。15番手にルフトシュトロームとニシノストーム。17番手がサトノインプレッサで最後尾にウイングレイテストという隊列。前半の800mは46秒0のミドルペース。
　前の方の隊列は変化がないまま直線に。残り400mあたりから逃げたレシステンシアが追い出しましたが,マークしていたラウダシオンも楽についていき,2頭が抜け出す形に。ラウダシオンが悠々とレシステンシアを差して優勝。逃げ粘ったレシステンシアが1馬身半差で2着。4分の3馬身差の3着争いは激戦でしたが外から伸びてきたギルデッドミラー。内を捌いてきたタイセイビジョンがハナ差で4着。
　優勝したラウダシオンはこれが4勝目で重賞初制覇を大レースで達成。このレースはレシステンシアの能力がほかに対して一枚上とみていました。それを楽にマークしていくことができたのが勝因でしょう。逆にいえばレシステンシアは,ほかがついてくるのが厳しくなるくらいのペースで逃げた方がよかったのではないでしょうか。父は2011年に安田記念,2013年に阪神カップ,2014年に阪神カップ,2015年にジョージライダーステークスを勝ったリアルインパクトでその父はディープインパクト。馬名はグレゴリオ聖歌の続唱の名称。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　騎乗したミルコ・デムーロ騎手は大阪杯以来の大レース制覇。第24回からの連覇でNHKマイルカップ2勝目。管理している斉藤崇史調教師は秋華賞以来の大レース3勝目。NHKマイルカップは初勝利。

　バディウAlain Badiouがスピノザの幾何学的方法を理解することができなかった,あるいはそれに同意することができなかった理由としては,僕には以下の二点が考えられます。
　第一に,スピノザのような幾何学的方法を採用すると,そのすべてを原因causaから結果effectusへ辿っていく必要が生じます。いい換えれば,すべてを演繹法によって論証していく必要が生じます。おそらく幾何学的方法の最大の特徴はこの点にあり,バディウは何らかの理由でそのことに同意できなかった可能性があります。この場合には,バディウは第一部公理三とか第一部公理四にはとくに同意することができないということになるでしょう。もしもバディウが,演繹法を用いずに,他面からいえば帰納法によって何事かを論証することができるという認識cognitioを有していたとしたなら,これらふたつの公理Axiomaについて,それに同意することができなかったというより,それらを理解することができなかったといういい方が,より成立することになるように僕には思えます。
　ただ,このことはメイヤスーQuentin Meillassouxがバディウの第一のテーゼとみなしている,数学が存在論であるということとはあまり関係をもたないようにも感じられます。これらの公理は,一の存在論を採用する場合にだけ成立しなければならないというわけではなく,もし多の存在論を採用する場合にも,成立し得る,少なくとも成立し得る場合があるのではないかと僕には思えるからです。バディウは,多の存在論を採用するときは,その多は空からなるのでなければならないといっていますが,演繹法を採用したら空を規定することが不可能になるという理由が僕には見当たらないのです。
　第二の点は,それをバディウの存在論から解する方法です。この場合は,幾何学的方法一般というよりは,バディウが同意することができなかったのは,スピノザの幾何学的方法であったということになります。スピノザの幾何学的方法は,実在的なものについてはまずそれをまとめて規定してしまうので,空を規定する余地がなくなるのです。多が空から成立するということは,バディウの存在論すなわち数学の最も基本の原理を構成するので,これは大問題であった筈です。

おまえの家④＆理論的ライバル

　③で,ギターをやめた,つまりプロのミュージシャンになることを諦めたと伝えたおまえと,それを伝えられた歌い手との間には沈黙が流れます。とくに歌い手の方にとって,それは衝撃的な告白だったと思われるのです。というのも,お前と歌い手は,以前は同じように音楽に夢中になっていました。①でいったように,歌い手の方は現在は別の仕事をしています。それは,もしかしたらお前と同じように夢を追っていたのを諦めた末の結果だったかもしれません。そしてもしもそうであったなら,歌い手は自分の夢をおまえに託していたかもしれないからです。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　そして歌い手はお前の部屋を見回します。

　　　　　部屋の隅には　黒い革靴がひとつ
　　　　　くたびれて　お先にと休んでる
　　　　　お湯のやかんが　わめきたてるのを　ああと気がついて
　　　　　おまえは　笑ったような　顔になる

　靴は当然おまえの靴です。くたびれて,という表現から,もうずいぶんと使われていること,もしかしたらさっきまで使われていたかもしれないことが分かります。そしてそのとき,②で沸かし始めたお湯が沸き,やかんから音が鳴りました。おそらくおまえは火を消しにいったことでしょう。歌い手はさらに部屋を見渡します。

　　　　　なにげなく　タンスに　たてかけた　ギターを
　　　　　あたしはふと見つめて　思わず思わず　目をそむける
　　　　　あの頃の　おまえのギターは　いつでも
　　　　　こんなに磨いては　なかったよね

　この楽曲の中で僕が最も好きな部分がここです。昔は磨くことも忘れてただ弾くばかりだったギターが,今では大切に磨かれてタンスに立てかけてあるのです。おまえがギターをやめたときの心境が,あるいはそれを歌い手に告白したきりガス台の火を見つめ続けたおまえの心境が,ここには凝縮されているように感じられます。

　近藤はこのようにバディウAlain Badiouの主張の概略を示した上で,現時点でその唯一の正当な理論的なライバルはスピノザの『エチカ』であるといっています。本当に『エチカ』がバディウの理論構成に対する唯一のライバルであると断定してよいのかは僕には分かりません。ただ,バディウに対して『エチカ』が論理的なライバルであるという点だけをここでは重視します。そしてバディウは『エチカ』が自身に対する理論的なライバルであることを自覚していたから,いくつかの著作でスピノザの存在論を批判しているのだと近藤はつけ加えています。バディウがどのようにスピノザを批判しているのかは分かりませんが,批判しているということ自体は確かなことでしょう。そしてバディウがスピノザの存在論を批判するとき,その中心となっているのは幾何学的方法であるとされています。
　ここまでの事情を綜合した上で,『主体の論理・概念の倫理』を考察したときの補足を開始します。
　まず,バディウは集合論を数学だと思っているので,スピノザの公理論は分からないというとき,バディウは公理論を数学とは認めないという意味ではなかったことになります。これはバディウが数学は存在論であるというときの数学が,公理論的集合論でなければならないといっていることから明白です。当時の考察においては僕はあたかも公理論と集合論が数学的論理として対立するものであるという解釈をして,それがなぜ対立するのかを謎と感じていたのですが,実際にはそういう対立はなかったことになります。いい換えれば,集合論を公理論的に示すことは可能であると解することができるということになります。
　では鼎談の中でバディウは公理論は分からないと近藤が言ったとき,その主旨がどこにあったのかといえば,それはスピノザの幾何学的方法を理解することができなかったという点にあったのでしょう。もう少し正確にいうと,それを理解することができなかったというよりは,それに同意することができなかったと解しておく方がいいかもしれません。そしてなぜ幾何学的方法に同意できなかったのかといえば,数学すなわち存在論という観点に理由があったのです。

歓喜と落胆＆多と集合論

　もしも派生感情を個別の派生感情として考えた場合には,歓喜gaudiumと落胆conscientiae morsusは,安堵securitasと絶望desperatioの派生感情でもあり得ます。より正確にいえば,歓喜は絶望の派生感情であり得ますし,落胆は安堵の派生感情でもあり得るのです。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　もちろんどちらの場合であれ,それらの歓喜ないしは落胆が発生するためには,前もってそのことについての希望と不安がそれを感じる人間のうちにあるのでなければなりません。もっともこのことは,ある人間のうちに安堵が生じる場合も絶望が生じる場合も,前もってそれに対する希望spesと不安metusがその同じ人間のうちにあるのでなければならないと僕が考えているということから当然だといえます。そしてこのことは,安堵,絶望,歓喜,落胆のすべての感情affectusに一般的に妥当します。一般的に妥当するということは個別にも妥当するということですから,僕たちがこれらの感情に刺激されるafficiとき,不安と希望が直接的な起成原因causa efficiensとなって安堵を感じたり絶望を感じたりすることもあれば,歓喜を感じたり絶望を感じたりする場合もあるのです。僕はこの点までは畠中の見解opinioに同意します。
　しかし,安堵と絶望は個別的な場合でも希望と不安が直接的な原因であるのに対し,歓喜と落胆の場合はそうとはいえません。希望と不安から歓喜や落胆が個別的に生じる場合もあるのですが,希望と不安からまず安堵を感じ,さらにこの安堵が原因となって落胆が生じるという場合がありますし,逆に希望と不安から絶望が生じ,この絶望が原因となって歓喜が生じるという場合もあるのです。このゆえに僕は,希望と不安から生じる喜びlaetitiaが安堵で,悲しみtristitiaが絶望であると解します。これらの感情に関係する畠中説の不都合は,単にスピノザがこれらの感情をどのように記述しているのかという点だけにあるのではありません。というよりも,このような個別の事情があり得るから,スピノザは安堵と絶望を同じように記述し,歓喜と落胆はそれとは別の仕方で同じように記述したのではないでしょうか。

　空というのは当然ながら実在的なものではありません。これは哲学的に考えれば当然のことですし,数学でもおそらくそうなのでしょう。したがって,多が空でなければならないのであれば,それは実在的なものだけを対象とするわけではありません。むしろ非実在的なものを対象とする必要があります。バディウAlain Badiouは数学は存在論であるといっているわけですから,その存在論というのは,実は非実在的なものを対象とした,少なくとも非実在的なものを対象として含む存在論でなければならないのです。よって,存在するものだけを対象とするような存在論いい換えれば数学は,バディウが求めている数学ではありませんし,バディウが求めている存在論ではないのです。
　このためには,非実在的なものを対象として思考することができるような方法があるのでなければなりません。そしてバディウはその方法として,公理論的方法を示しています。なぜなら公理論的方法は,実在的な対象を事前には要請しないからです。このことは『エチカ』で考えても理解することができます。『エチカ』の方法は明らかに公理論的方法であるといえます。そのとき,たとえば第一部定義三は,実体substantiaが実在的realiterであるということを前もって要請しているわけではなく,それ自身のうちにあり,それ自身によって概念されるもののことを実体というということだけを示しているからです。
　これでみれば分かるように,バディウは公理論的方法を否定しているわけではありません。『主体の論理・概念の倫理』を考察したときには,あたかもバディウは集合論を数学と認め,公理論を数学とは認めないというように僕は認識していたのですが,それは誤りです。バディウが認めないのは公理論一般ではなく,公理論の中でもスピノザのような方法,方法としていえば幾何学的方法といわれる方法についてのようです。しかしこのことについてはあとでまとめて考察します。
　数学において多を扱う形式学は集合論であるというのがバディウの最後の主張です。したがって数学はあるいは存在論は,公理論的集合論でなければなりません。これがバディウの主張についての近藤の集約の概要になります。

日刊スポーツ賞東京湾カップ＆多と空

　昨日の第34回東京湾カップ。
　チョウライリンは立ち上がって2馬身の不利。外の方から被せつつ強引にサンスクリットがハナへ。2番手にはマーヴェルクエストとエメリミットとレイワデジタル。2馬身差でプレストシャインとアマルインジャズ。7番手にデスティネとシナノパワー。3馬身差でヘブンリーキス。10番手にマンガン。4馬身差でドテライヤツ。6馬身差の最後尾にチョウライリン。ハイペースでした。
　3コーナーからエメリミットが逃げるサンスクリットに並び掛けていき,コーナーの途中で前に出て先頭で直線へ。この時点で追ってきたのはデスティネでしたが,直線に入るとエメリミットが突き放して抜け出しました。大外から差し脚を伸ばしてきたのがマンガンで,デスティネを差して2番手に上がるとさらにエメリミットとの差もぐんぐん詰めていき,ついには差し切って優勝。エメリミットがクビ差で2着。デスティネが3馬身差で3着。
　優勝したマンガンは南関東重賞初制覇。このレースは南関東重賞で入着していた馬と,条件戦を勝ち上がってきた馬との激突。結果的に前者が1着と2着,後者が3着となりましたから,すでに南関東重賞に出走して馬たちの方が,平均的な能力は上位であったと考えてよいでしょう。これまでの戦績から,トップクラスの馬たちとは歴然とした差があると考えなければならないでしょうが,末脚が鋭いタイプなので,極端なハイペースのレースになれば,そうした馬たちを相手にしても勝つというケースがあり得るかもしれません。母の父はアグネスタキオン。馬名は麻雀の満貫だと思います。
　騎乗した川崎の山崎誠士騎手は先週の羽田盃に続いての南関東重賞15勝目。第30回以来4年ぶりの東京湾カップ2勝目。管理している川崎の田島寿一調教師は南関東重賞2勝目。東京湾カップは初勝利。

　多の存在論と集合論とを結びつけるのは,空あるいは空虚という概念notioです。ただし僕は数学には詳しくないので,数学における,あるいは集合論における空という概念がいかなるものであるかよく分かりません。また,この点に関しては『〈内在の哲学〉へ』でも『主体の論理・概念の倫理』でも説明されていません。そこで,多の存在論と集合論がいかにして空という概念によって結束するのかということは脇に置いておき,バディウAlain Badiouがそのようにみなす論理構成だけを確認しておきます。これについては近藤が簡潔な説明を与えています。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　まず基本となるのが,バディウが第一のテーゼとして,数学は存在論である,というときの,存在existentiaが多であるということです。このとき存在が多であるということのうちには,存在は一ではないという意味が含まれているのですが,たぶんバディウはそのような消極的な意味として存在は多であるといっているのではなく,積極的な意味において存在を多と規定しているものと僕は解します。
　次にバディウは,この多は一の多ではないという意味のことを主張します。ここでも一の多というのが具体的に何を意味するかということは僕には不明です。ただ,たとえばあらゆる様態modusは多として存在するけれども,それはすべて様態的変状modificatioに様態化した一としての神Deusであるというようにスピノザの哲学を解すれば,スピノザの哲学は多ではあり得ても一の多であるということは可能なのであり,バディウはこのような意味での多も認めないというように僕は解します。ただしバディウがいっているのは,多は一の多ではないということよりも,多の多であるという点にあると解するのが適切かもしれません。つまりここでもバディウは消極的に,多は一の多ではないといっているのではなく,積極的に多は多の多であるといっているのだと解するのがよいのだろうと僕は思っています。
　存在が多の多である場合は,多は空から成立しなければならないことになります。なぜそうなるのかは分かりませんが,バディウはそのように主張していると近藤はいいます。同時にそれには疑問を投げ掛けないので，この点には合理性があるのだと思います。

農林水産大臣賞典兵庫チャンピオンシップ＆集合論と存在論

　第21回兵庫チャンピオンシップ。
　マカオンブランが先頭に立ったところ,ダノンファラオが競りかけていきました。しかし譲らなかったマカオンブランの逃げとなり,控えたダノンファラオが2番手。3馬身差でバーナードループ。4番手にヒルノマリブで5番手にピスハンド。2馬身差でガミラスジャクソン。2馬身差でアカリン。2馬身差でハルプモント。9番手はヴィクトリアグラスとサンデーミラージュ。2馬身差でジェッティーとニコラスタッカートが最後尾を併走。スローペースだったのではないかと思います。
　レースが動き出したのは2周目の向正面に入ってから。前の2頭が一時的に3番手を4馬身ほど離し,3番手のバーナードループがそれを追っていく形に。3コーナーを回るとダノンファラオが外から先頭に出て,マカオンブランはここで一杯。サンデーミラージュが後方から追い上げてきました。ダノンファラオが先頭で直線に入り,バーナードループは外の方へ。このコーナーワークで差が開きました。しかしバーナードループは少しずつ内に斬り込みながらではありましたがダノンファラオを差し切ることに成功して優勝。ダノンファラオがクビ差で2着。サンデーミラージュが９馬身差の3着。
　優勝したバーナードループは重賞初挑戦での勝利。このレースはダートのオープンで実績を上げた馬が不在でしたので,1勝クラスを勝ち上がった馬の中での争い。この馬は新馬で2着になった後,連勝できていましたから,魅力という点では最も高かった馬です。ただそれはこのメンバーの中でということ。2着馬は前走のオープンで勝ち馬から1秒差というレベルなので,それに僅差での勝利は,上昇度を加味してもそこまで高くは評価できません。新馬を2着になったときは1秒6の差をつけられていて,その馬はすでにオープンを勝っていますから,3歳馬の全体の中でトップクラスということは考えにくいのではないでしょうか。父はロードカナロア。祖母がステラマドリッド。母の2つ上の全姉に2002年のJRA賞の最優秀4歳以上牝馬のダイヤモンドビコー。馬名はオリオン座にある星雲の名称。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　騎乗したクリストフ・ルメール騎手は第20回からの連覇で兵庫チャンピオンシップ2勝目。管理している高木登調教師は兵庫チャンピオンシップ初勝利。

　バディウAlain Badiouの主張の主旨がどういう点にあったと解するのが,ここでの考察と関連して適切であるかは分かりました。しかしなぜそれが数学の一理論である集合論と関係を有さなければならないかは不明です。
　これについてはバディウ自身は,バディウがいう存在論の観点から説明しています。存在論というのを哲学的に,あるいは形而上学的に解した場合の広い意味での存在論のうち,バディウが真の意味で存在論であると認めるのは多の存在論でした。バディウはその存在論が一に依拠せず多を思考するためには,公理化された数学でなければならないと主張していたのですが,それと同時に,この存在論すなわち数学が純粋な多の思考として実現されるためには,カントールの数学が用いられなければならないともいっています。ここでバディウがいうカントールの数学というのが,集合論に該当します。また,純粋な多の思考というのが何を意味するかは微妙ですが,一に依拠しない思考というようにここでは解しておきます。それと同時にそこには,数学的な理念とか数学的な形式という意味も含まれているでしょう。もちろんここでいう数学とは,数学全般をいうのではなく,集合論を意味することになります。というかこの文脈においては,集合論だけが数学であるとバディウはみなしていると解釈しておく方が適切でしょう。したがって『主体の論理・概念の倫理』における鼎談で,バディウは集合論を数学だと思っていると近藤が発言していたことには,一定の合理性があるということになるでしょう。
　バディウは,存在論は数学の歴史において主題化はされてこなかったのだけれども,それは実現ないしは達成されてきたのだといっていました。バディウがそのようにいうときに念頭に置いていたのが,カントールの数学でありまた集合論であったということになるでしょう。バディウのこの主張に関しては,完全に達成されたとか完全に実現されたという意味ではなく,これからも達成されていくしこれからも実現されていくと解するのが適切だと僕は考えますが,その際にも,それは集合論によって達成されるのだし,実現されるのだと解するのがよいでしょう。

農林水産大臣賞典かしわ記念＆バディウの主張

　第32回かしわ記念。
　このメンバー構成であればワイドファラオの逃げは予想されたところ。位置を取りにいったルヴァンスレーヴが2番手。2馬身差でアルクトス。3馬身差でモズアスコット。5番手にケイティブレイブで6番手にサンライズノヴァ。4馬身差の最後尾にナンヨーオボロヅキという隊列。前半の800mは49秒6のスローペース。
　3コーナーを回るとまずアルクトスが動き,2番手のルヴァンスレーヴの外で併走。ここでルヴァンスレーヴはやや苦しくなり,逃げたワイドファラオと2番手の2頭の差がやや開きました。ルヴァンスレーヴの内からはケイティブレイブが進出。直線に入るとルヴァンスレーヴは脱落。残ったケイティブレイブとアルクトスも軽快に逃げたワイドファラオを追い詰めるには至らず,楽に逃げ切ったワイドファラオが優勝。内を突いたケイティブレイブが2馬身差で2着。直線で大外から伸びたサンライズノヴァが1馬身半差の3着に届き,アルクトスは半馬身差で4着。
　優勝したワイドファラオは昨年のユニコーンステークス以来の勝利。重賞は3勝目で大レースは初勝利。このレースは能力ではルヴァンスレーヴ,モズアスコットの順でしたが,ルヴァンスレーヴは1年5ヶ月ぶりの実戦,モズアスコットにはコーナーを4度回るレースとそれぞれに課題があり,その課題を克服することができませんでした。ワイドファラオは展開も味方につけて,それ以外の馬を降したという内容。ですから着順や着差の通りに能力を評価するのは危険ではないかと思います。母の父はアグネスタキオン。母の従兄に2009年にカペラステークス,2010年に北海道スプリントカップを勝ったミリオンディスクで,その半妹に2013年に関東オークスを勝ったアムールポエジー。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　騎乗した福永祐一騎手は皐月賞以来の大レース35勝目。第15回以来17年ぶりのかしわ記念2勝目。管理している角居勝彦調教師は日本ダービー以来の大レース38勝目。かしわ記念は初勝利。

　『主体の論理・概念の倫理』の三者の鼎談の中で,バディウAlain Badiouは数学を集合論だと思っているので,公理論的方法を理解していないという主旨の発言が近藤からありました。このために僕は集合論が公理論と対立的な数学の理論であると判断してしまい,集合論と公理論は相容れないふたつの理論であると思ってしまったのです。ですが実態はそうではなかったようです。このときに近藤がそれを理解することができないと言ったのは,公理論一般ではなく,スピノザのようなあるいは『エチカ』のような公理論のことで,幾何学的方法によって,すべてを演繹的に証明していく方法のことだったようです。
　バディウは,数学は存在論であるというテーゼを立て,より正確にいえば,メイヤスーQuentin Meillassouxはバディウが,数学は存在論であるというテーゼを立てているとみなしたのですが,その存在論は多の存在論です。そしてバディウは,一に依拠しないで純粋な多を思考するためには,存在論は公理化された数学でなければならないとも主張しています。
　この主張もまた,もしそれを哲学的に,あるいは形而上学的に理解しようとすれば,不思議に感じられるかもしれません。すでに説明したように,スピノザの哲学における存在論は,究極の一の存在論といえるべきものであり,それは『エチカ』においては公理系に基づいて論証されているからです、ですがここでバディウがいいたいのはそういうこと,つまり存在論は公理系に基づいて論証されなければならないということではないのです。この文脈の中でバディウの主張を理解するなら,それはおそらく,スピノザは公理系に基づいてすべてを論証しているけれど,それは数学ではないということなのです。そしてバディウは数学は存在論であるといっているのですから,それは存在論ではないということなのです。つまり仮に公理系に基づいてすべてを論証するのであったとしても,スピノザのような方法で行うと,それは数学ではなくしたがって存在論でもなくなるので,もし公理論的に存在論を展開しようとするのであれば,それとは別の方法が必要であるということが,バディウがいいたかったことなのだと解するのが適切です。

農林水産大臣賞典かきつばた記念＆一致と反撥

　第22回かきつばた記念。
　リアンヴェリテはハナを奪うために鞭を入れていましたが,外のラプタスの方がダッシュに優り,１コーナー手前で前に出てラプタスの逃げ。リードも2馬身くらいに。2番手に逃げられなかったリアンヴェリテとマイタイザン。3馬身差でラブカンプー。2馬身差でノボバカラ。2馬身差でドリームドルチェとモズオラクルとアディラート。4馬身差でサンデンバロン。2馬身差でメモリージルバ。2馬身差の最後尾にペイシャゲランと,この距離にしては縦長の隊列に。ミドルペースでした。
　リアンヴェリテは向正面で下げ,単独の2番手となったマイタイザンは3コーナーを回ると一杯。ノボバカラが2番手に上がり,外から巻き返したリアンヴェリテ,内からドリームドルチェの追い上げ。ラプタスのリードは一時的には詰まりましたが,直線に入るとまた引き離し,鋭く逃げ切って優勝。ノボバカラが3馬身差で2着。内を回ったドリームドルチェが5馬身差の3着で外を回ったリアンヴェリテは4分の3馬身差で4着。
　優勝したラプタスは黒船賞からの連勝で重賞2勝目。逃げることがベストなのは分かっていましたので,今日はやはり逃げたかったであろうリアンヴェリテとの逃げ争いが最大の焦点。発馬後の加速力で早々に決着をつけた時点で,今日のメンバー構成から勝利を決定づけたといっていいでしょう。逃げられなかった場合に同じように力を発揮することができるかどうかは未知ですから,課題はまだ残っていると考えておいた方がよいでしょう。父はディープブリランテ。5代母がバウンドトゥダンスとファーストアクトの祖母にあたります。Raptusは衝動。
　騎乗した幸英明騎手は第13回以来となる9年ぶりのかきつばた記念2勝目。管理している松永昌博調教師はかきつばた記念初勝利。

　自身の学説を哲学的に基礎づけようと意図したフロムErich Seligmann Frommが,そのためにスピノザとアリストテレスAristotelēsを数多く引いたのは,フロムの学説を哲学的に基礎づけるためには,スピノザの哲学とアリストテレスの哲学が有効であるとフロム自身が考えたからです。したがって少なくとも,フロムの学説を基礎づけるという点においては,スピノザの哲学とアリストテレスの哲学は一致するのです。だからといってプラトンPlatoの哲学はそのために有益ではないということにはなりませんが,スピノザの哲学とアリストテレスの哲学が,存在論では一致しないからといって,ほかのすべての面においても一致しないというわけではないということは,この例から明らかでしょう。そしてこのような一例があるのだとすれば,スピノザの哲学とプラトンの哲学は,存在論においては一致する面があるにしても,ほかのすべての面において一致するとは限らないということも明らかだと思います。さらにつけ加えれば,アリストテレスの存在論というのはプラトンの存在論に対する批判から現れたものだと僕は思いますが,だからといってプラトンの哲学とアリストテレスの哲学は,すべての点において反撥し合うことになるというわけではなく,一致をみる部分もまた存在するでしょう。これらの点ついてはくれぐれも勘違いしないように注意してください。
　バディウAlain Badiouの存在論に話を戻します。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　『主体の論理・概念の倫理』を巡る考察の中でバディウに言及したとき,僕にとって最も謎であったのは,スピノザの公理論とバディウの集合論が対立するという点でした。それがどういった謎であったか詳しくはそのときの考察を読んでもらうほかありませんが,簡単にいえば僕は,集合論を公理系によって記述することが不可能なこととは思えなかったために,公理論と集合論が対立しなければならない理由というのを見出すことができなかったのです。
　『〈内在の哲学〉へ』を読む限りでは,僕が謎と感じたことは実際には謎ではなく,僕が考えていた通りに成立するのです。つまり集合論を公理系を用いて記述するということは可能で,そのような意味で公理論と集合論が対立するのではないのです。

天皇賞(春)＆究極の一

　第161回天皇賞(春)。
　トーセンカンビーナとメイショウテンゲンは発馬のタイミングが合わず1馬身の不利。まず先頭に立ったのはダンビュライトで,2番手のスティッフェリオに対して4馬身くらいのリードをとっていきました。ですが1周目の正面に入って押さえきれなかったキセキが上昇。1コーナーを前にかなり外の方からダンビュライトの前に出て,そこからはキセキの逃げに。3馬身差でダンビュライト,5馬身差でスティッフェリオ,4馬身差でモズベッロで5番手にハッピーグリンという具合に,前は縦長になりました。3馬身差でユーキャンスマイルとシルヴァンシャー。2馬身差でフィエールマン。9番手はエタリオウとミッキースワロー。11番手にミライヘノツバサとメイショウテンゲン。13番手がトーセンカンビーナで最後尾にメロディーレーンという隊列に。最初の1000mは63秒0のスローペース。ただし中盤もラップが落ちませんでした。
　キセキは最後の直線に向いても先頭。ダンビュライトが2番手でその外にスティッフェリオ。ダンビュライトは苦しくなって,スティッフェリオがキセキを差して先頭に。追ってきたのは最内に進路を取ったユーキャンスマイルと外を伸びたミッキースワローとフィエールマン。抜け出したスティッフェリオに追いついたのはフィエールマンで優勝争いはこの2頭。フィニッシュ前は馬の首の上げ下げで抜きつ抜かれつになりましたが,フィニッシュの時点ではフィエールマンが前に出ていて優勝。スティッフェリオがハナ差の2着。外のミッキースワローが2馬身半差の3着で内のユーキャンスマイルはクビ差の4着。
　優勝したフィエールマンは昨年の天皇賞(春)以来の勝利で大レース3勝目。このレースが今年の初戦でしたが,間隔を開けて使いながら成績を残してきた馬でしたから,その点はあまり不安要素ではありませんでした。案じていたのは大外枠を引いていたことで,2着馬とはもう少し能力差がある筈なので,大接戦になった要因はそこだったかもしれません。一時的に縦長の隊列になったことは,大外枠のこの馬にとっては有利に働いたのではないでしょうか。父は第133回を制したディープインパクト。Fierementはイタリア語で燃え上がり。音楽用語です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　騎乗したクリストフ・ルメール騎手はフェブラリーステークス以来の大レース制覇。第158回,159回,160回に続く四連覇で天皇賞4勝目。天皇賞(春)は連覇で2勝目。管理している手塚貴久調教師は昨年の天皇賞(春)以来の大レース7勝目。天皇賞は2勝目で天皇賞(春)は連覇で2勝目。

　実在する実体substantiaは神Deusだけです。そして神以外に何かが存在するとすれば,神の本性essentiaを構成する無限に多くのinfinita属性attributumを除けば,様態modiだけです。様態は実体の変状substantiae affectioです。実在する実体が神だけである以上,実在する様態は神の変状だけであることになります。したがって様態とは,神があるいは神のある属性が様態に変状したものです。あるいは様態とは,様態的変状modificatioに様態化した神あるいは神の属性です。これでみれば神だけが実在するといっているのと大差ない,あるいはもっと極端に,神だけが存在するといっているとも解せるでしょう。このような意味で,スピノザの存在論は一の存在論であることになりますし,ある意味では徹底した一の存在論であるとさえいえるのです。僕は,内在の哲学を究極まで推進すれば,その哲学における存在論は一の存在論にならざるを得ないといいました。スピノザの哲学は究極的な内在の哲学ですから,その存在論が徹底した一の存在論となっていることは,当然といえば当然といえるかもしれません。
　先に進む前に,ここで注意しておいてもらいたいことがあります。僕は一の存在論の代表としてプラトンPlatoを,そして多の存在論の代表としてアリストテレスAristotelēsの名前をあげました。これでみれば分かるように,スピノザの哲学の存在論というのは,プラトン的なものであり,アリストテレス的なものではありません。ですがこれはその哲学の存在論を切り取った場合のことであって,スピノザの哲学がプラトン的な哲学であり,アリストテレス的な哲学ではないということではありません。むしろその哲学の中の存在論の部分だけを抽出して,スピノザの哲学はプラトン的だといったのと同じように,別のある部分だけを抽出すれば,スピノザの哲学はプラトンの哲学と相反するという場合があるでしょうし,逆にアリストテレスの哲学に近いという場合もあるでしょう。
　こうしたことをすべて検証していくことは僕の力では不可能ですし,現在の考察の観点からいえば不要です。一例だけ挙げれば,フロムは社会心理学者ですが,自説を哲学的に裏付けようという意図をもっていました。そこで傍証されるのはスピノザでありアリストテレスです。

印象的な将棋⑯－６＆スピノザの存在論

　⑯－５の第2図は,先手が放置して☖５七歩成と王手をされて玉を吊り出されては大変です。かといって☗５六同歩と取るのは☖４六角で終了です。なので☗５四飛と王手を掛けるのはこの一手。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　これに対して☖５二飛は飛車交換して先手がよいでしょう。☖５二金も☗６三銀や☗７一角が残るので☖４一玉と逃げました。
　ここも☖５七歩成とされると☗同飛は☖４六角があります。なので☗５六飛と歩を払いました。これが銀取りになっているので☖６五銀はこの一手。
　今度は☗８六飛からの飛車交換は後手に分がありそうです。右に逃げる手はあったかもしれませんが,成れるのですから☗５三飛成とするのは自然に思えます。
　後手はこれが読み筋だったようで☖５六歩。☗同歩は☖３五角で終了なので☗７九王と早逃げしました。それでも後手は☖３五角。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　後手の攻めは快調ですが,先手が悪くなったというわけでもありませんでした。

　第一部公理一の意味は,存在するものは実体substantiaであるか,そうでなければ実体の変状substantiae affectioである様態modiであるかのどちらかであるということでした。つまりそれ自身のうちにあるesse in se実体と実体のうちにある様態のどちらかだけが存在するのであり,それ以外には何も存在しないのです。これは存在するあらゆるものが実体のうちにあるという意味で,内在の哲学の論拠になるのですが,それと同時に,それ自身のうちにあらゆるものを含む実体が存在するという意味で,一の存在論でもあるのです。内在の哲学を採用するとその存在論が必ず一の存在論になると結論していいのかどうかは僕には分かりません。しかし少なくともスピノザの哲学のように,内在論を徹底的に推進していけば,その存在論が一の存在論にならざるを得ないのは間違いないところだと思います。
　さらにこの公理Axiomaには僕が第一部公理一の実在的意味といっているものが含まれています。すなわち第一部公理一を公理として採用する限り,実体が存在するか,そうでなければ何も存在しないかのどちらかでなければならないということが帰結するのです。しかし何も存在しないということはそれ自体で不条理でしょう。したがって実体は確実に存在するのです。いい換えれば,それ自身のうちにあるものは確実に存在するのです。つまりそれ自身のうちにあるものというのは,仮定としてあるいは名目的にそのようにいわれるのではなく,実在的なものとしてそのようにいわれていると解さなくてはなりません。こちらの説明の方が,なぜスピノザの哲学が,多の在論ではなくて一の存在論であるのかということを分かりやすく理解できるかもしれません。
　何度かいっているように,『エチカ』の第一部の最初の方には,実在的な意味はもたず,名目的にそのようにいわれている定理Propositioがいくつか存在しています。しかしそれが実在的な段階に突入すると,一の存在論はさらに徹底されます。それが第一部定理一四および第一部定理一四系一で,そこでは存在する実体は神Deusだけであるということと,神は唯一であるということが主張されています。つまり単に実体のうちにすべてが存在するだけでなく,実体自体が一なのです。