よく、累積バグ数をかいて、S字カーブとかいうけど、
あのカーブの数式と、その係数の意味がわかっているのか、
意識あわせしたいことがあったので、
ここで、みなさんとシェアしたいと思います!
■そもそも、「ソフトウェア信頼度成長モデル」の式は?
物事を知るには、まずは、Wikipediaだ
(っていうと、大学の先生からは怒られるが、ふつうそうだ)
Wikipediaの信頼度成長曲線によると(以下太字は、上記サイトより引用)
信頼度成長曲線(しんらいどせいちょうきょくせん 英:Software Reliability Growth Curve)とは、横軸に日付、テスト時間、またはテストケース数、縦軸に累積バグ発見数をとったグラフ。S字の成長曲線を描くことが多い。
プロジェクトの進捗状態の確認などに用いる。
決定論的モデルとして、最小二乗法でゴンペルツ曲線やロジスティック曲線に近似したり、確率モデルとして、非同次ポアソン過程モデルなどで表したりすることにより、現在の状況から今後の予想を立て、テスト進捗管理、バグ収束率の予測、残バグ数の予測などに用いることもある。
収束を見る場合に、横軸に日付を使った場合、テストをしていないからバグが出ないのか、テストをしてもバグが出ないのかの区別がつかないという問題がある。
・・・式がない。こまった・・・
式が出ている論文をさがすか・・・
ここ
ソフトウェア信頼度成長モデルに基づく最適リリース問題
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/0680-06.pdf
ソフトウェア信頼度成長モデルは4つ知られている。
その式を上記論文から切り貼りして、引用する。

ちなみに、この4つのグラフ、求められるツールがあるみたいなんだけど(このリンク先)
以下の式の変数の意味がわかると、Excelで求められるので、ま、いっか・・
■4つの式のうち、これから説明するもの
まず、指数形がキホン。このa,bの意味をこれから説明する。
その後なんだけど・・・
修正指数形ソフトウェア信頼度成長モデルは、
そのΣが、i=1から2(1と2)なので、その式は
a*( p1(1-exp(-b1t)) + p2(1-exp(-b2t)) )
となる。つまり、指数形a(1-e^-bt)に確率p1,p2かけているに過ぎない
遅延ソフトウェア信頼度成長モデルは、
指数形のexpの係数に(1+bt)をかけて、時間と共に減少率をコントロールしている
だけで、aとbの意味は変わらない
ので、指数形のa,bのあと、習熟S字のcの値を説明する。
■aの値
指数形: H(t)=a(1-exp(-bt)) (eの-bt乗をexp(-bt)と表現)
指数にマイナスがつくと分数になる(10の-1乗=0.1=1/10)ので
=a(1-1/exp(bt))とかける。
ここで、tが大きくなると、
exp(bt)は、指数関数的に大きくなるはず
(expは指数関数ですから)
ってことは 1/exp(bt)は小さくなる・・・小さくな~る、小さくな~る
(たとえばb=1なら、tが1なら1/e、tが100ならeの100乗分の1)
→かぎりなく0に近づく
ってことは、1-1/exp(bt)は、1にかぎりなく0に近い数を引くので、
1に限りなく近くなる。
ちなみにはじめは、b=0、t=0なので、1-1/exp(bt)=1-1/exp(0*0)=1-1/1=0
よって、この曲線は、a*0からa*1に限りなく近くなるまで
0≦a(1-exp(-bt))<a
という範囲で動く。aは限りなくその点に近づくがその点にならない、収束ポイント
→ということは、バグの最終的な累積数となる。
■bの値
tは、日数、時間数、いろいろあるけど、結局同じ形になるといっている
→こうなる理由は・・・bで値を吸収しているから。
つまり、bの値で曲線の形(収束の速さ)を制御している。
たとえば、
a=30(バグは最終的に30個)
t=10(10日でバグだし)
が、指数形になるとき、bの値の変化に応じて、どういう形になるかというのを
Excelで求めてみよう!
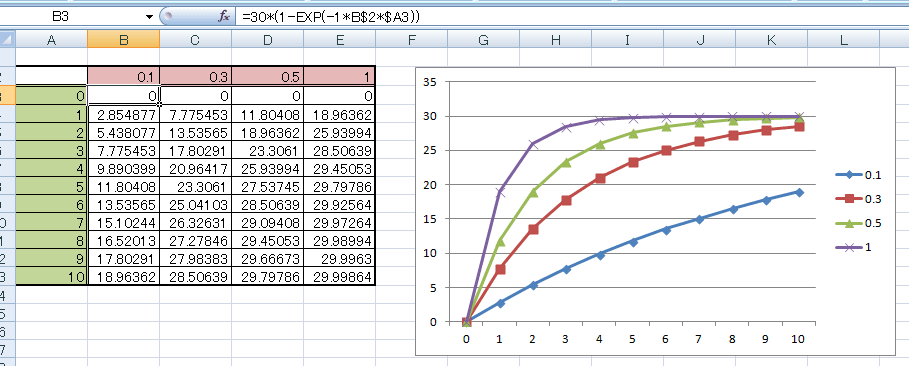
bが桁で、0.1,0.3,0.5,1と変化させている(行はt)
図を見ればわかるように、曲線の曲がり具合がbに左右している。
bを低くすると、ゆるやかになる。bを大きくすると、収束が早くなる
■cの値
図をみて?となったんじゃないだろうか・・・
S字でない。
そりゃ~そうですよ、だって
1-exp(-bt)
ですよ、指数関数を、
横軸tをb倍に拡大、
マイナスなんで、X=0で反転させて
expの係数にマイナス付いているから、こんどはY=0で反転させて、
1ずらして
a倍するだけですよ、
つまり、指数関数をごにょごにゅしてるだけじゃないですか!
そりゃー指数関数ですよ。
どこに、ぐにゃって曲げる要素がありますか?
ってことで、ぐにゃっと曲げる要素が、cです。
つまり、習熟の場合、
a(1-exp(-bt)) / (1+cexp(-bt))ってことは
指数形/(1+適当な係数c * 時間と共に指数的に小さくなるexp(-bt))
つまり、指数形を時間と共に指数的に影響が小さくなるcで割っているということです。
もすこし具体的に見ると、
はじめのころは、cの影響で割っているので、小さくなる
(1を足しているので、1以上の数なので、かならず小さくなる)
時間がずっとたつと、cの影響力がちいさくなり、ほぼ指数形になる
けっかとして、初めの頃、Cの影響で押さえ込まれ、ぐにゃっとなります。
a=30,b=0.8のとき、cを変えると、こんなかんじ。
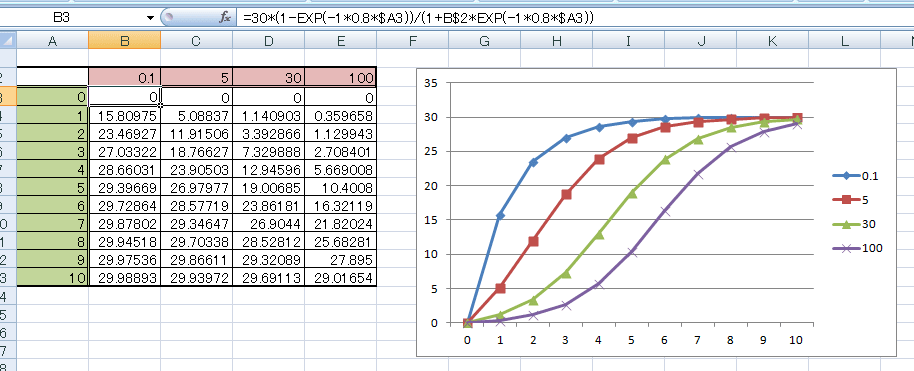
C=0.1だと、ほとんど変わらないけど、
C-30とかC=100は、いわゆるS字っぽいでしょ。
a,b,cの意味や、Excelでの図の書かせ方、わかりましたかあ?
あのカーブの数式と、その係数の意味がわかっているのか、
意識あわせしたいことがあったので、
ここで、みなさんとシェアしたいと思います!
■そもそも、「ソフトウェア信頼度成長モデル」の式は?
物事を知るには、まずは、Wikipediaだ
(っていうと、大学の先生からは怒られるが、ふつうそうだ)
Wikipediaの信頼度成長曲線によると(以下太字は、上記サイトより引用)
信頼度成長曲線(しんらいどせいちょうきょくせん 英:Software Reliability Growth Curve)とは、横軸に日付、テスト時間、またはテストケース数、縦軸に累積バグ発見数をとったグラフ。S字の成長曲線を描くことが多い。
プロジェクトの進捗状態の確認などに用いる。
決定論的モデルとして、最小二乗法でゴンペルツ曲線やロジスティック曲線に近似したり、確率モデルとして、非同次ポアソン過程モデルなどで表したりすることにより、現在の状況から今後の予想を立て、テスト進捗管理、バグ収束率の予測、残バグ数の予測などに用いることもある。
収束を見る場合に、横軸に日付を使った場合、テストをしていないからバグが出ないのか、テストをしてもバグが出ないのかの区別がつかないという問題がある。
・・・式がない。こまった・・・
式が出ている論文をさがすか・・・
ここ
ソフトウェア信頼度成長モデルに基づく最適リリース問題
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/0680-06.pdf
ソフトウェア信頼度成長モデルは4つ知られている。
その式を上記論文から切り貼りして、引用する。

ちなみに、この4つのグラフ、求められるツールがあるみたいなんだけど(このリンク先)
以下の式の変数の意味がわかると、Excelで求められるので、ま、いっか・・
■4つの式のうち、これから説明するもの
まず、指数形がキホン。このa,bの意味をこれから説明する。
その後なんだけど・・・
修正指数形ソフトウェア信頼度成長モデルは、
そのΣが、i=1から2(1と2)なので、その式は
a*( p1(1-exp(-b1t)) + p2(1-exp(-b2t)) )
となる。つまり、指数形a(1-e^-bt)に確率p1,p2かけているに過ぎない
遅延ソフトウェア信頼度成長モデルは、
指数形のexpの係数に(1+bt)をかけて、時間と共に減少率をコントロールしている
だけで、aとbの意味は変わらない
ので、指数形のa,bのあと、習熟S字のcの値を説明する。
■aの値
指数形: H(t)=a(1-exp(-bt)) (eの-bt乗をexp(-bt)と表現)
指数にマイナスがつくと分数になる(10の-1乗=0.1=1/10)ので
=a(1-1/exp(bt))とかける。
ここで、tが大きくなると、
exp(bt)は、指数関数的に大きくなるはず
(expは指数関数ですから)
ってことは 1/exp(bt)は小さくなる・・・小さくな~る、小さくな~る
(たとえばb=1なら、tが1なら1/e、tが100ならeの100乗分の1)
→かぎりなく0に近づく
ってことは、1-1/exp(bt)は、1にかぎりなく0に近い数を引くので、
1に限りなく近くなる。
ちなみにはじめは、b=0、t=0なので、1-1/exp(bt)=1-1/exp(0*0)=1-1/1=0
よって、この曲線は、a*0からa*1に限りなく近くなるまで
0≦a(1-exp(-bt))<a
という範囲で動く。aは限りなくその点に近づくがその点にならない、収束ポイント
→ということは、バグの最終的な累積数となる。
■bの値
tは、日数、時間数、いろいろあるけど、結局同じ形になるといっている
→こうなる理由は・・・bで値を吸収しているから。
つまり、bの値で曲線の形(収束の速さ)を制御している。
たとえば、
a=30(バグは最終的に30個)
t=10(10日でバグだし)
が、指数形になるとき、bの値の変化に応じて、どういう形になるかというのを
Excelで求めてみよう!

bが桁で、0.1,0.3,0.5,1と変化させている(行はt)
図を見ればわかるように、曲線の曲がり具合がbに左右している。
bを低くすると、ゆるやかになる。bを大きくすると、収束が早くなる
■cの値
図をみて?となったんじゃないだろうか・・・
S字でない。
そりゃ~そうですよ、だって
1-exp(-bt)
ですよ、指数関数を、
横軸tをb倍に拡大、
マイナスなんで、X=0で反転させて
expの係数にマイナス付いているから、こんどはY=0で反転させて、
1ずらして
a倍するだけですよ、
つまり、指数関数をごにょごにゅしてるだけじゃないですか!
そりゃー指数関数ですよ。
どこに、ぐにゃって曲げる要素がありますか?
ってことで、ぐにゃっと曲げる要素が、cです。
つまり、習熟の場合、
a(1-exp(-bt)) / (1+cexp(-bt))ってことは
指数形/(1+適当な係数c * 時間と共に指数的に小さくなるexp(-bt))
つまり、指数形を時間と共に指数的に影響が小さくなるcで割っているということです。
もすこし具体的に見ると、
はじめのころは、cの影響で割っているので、小さくなる
(1を足しているので、1以上の数なので、かならず小さくなる)
時間がずっとたつと、cの影響力がちいさくなり、ほぼ指数形になる
けっかとして、初めの頃、Cの影響で押さえ込まれ、ぐにゃっとなります。
a=30,b=0.8のとき、cを変えると、こんなかんじ。

C=0.1だと、ほとんど変わらないけど、
C-30とかC=100は、いわゆるS字っぽいでしょ。
a,b,cの意味や、Excelでの図の書かせ方、わかりましたかあ?


























