北大柔道部ログ

冬季居空間の重力井戸における四体問題の特殊解・特異解の求解方

2023-02-10 00:14:30

冬季居空間の重力井戸における四体問題の特殊解・特異解の求解方

北大柔道部

　極東地域の冬季には、居空間の中心にかなりの確率で重力井戸が出現する。これは多くの場合、四角錐台状の形で、その内部へ、傾斜した側面を経由して空間内の生物を引き寄せるという性質がある(A.Soga,2021)。これまでの観測から、気温に反比例して、その引力は大きくなることが知られている(K.Kojima,2022)。引き込まれた生物は基本的には二度と出て来ず、結果として内部でさまざまに干渉しあう。本レポートは、この干渉の末に到達する、安定した定常状態を解き明かしたものである。

　本計算では、空間は十分に広く、重力井戸の周りには十分な空間があり、ヒータやカーペットという、重力井戸に似た引力をもつものや、オフトゥンやマクラなど引力を打ち消すものは存在せず、電磁波によって、人のスピン方向を変えるテレヴィジョンなどの存在もないものとした。また、ヒトは極東原産で、エンリョウの法則に従うものと仮定した。

ヒトの存在状態はソガティンガー方程式の解によって記述されるが、未だに、解き方が確立されていない。そこで今回は、線形近似を用い、これを平面的に描画するソガティンガー・コジマ法を使用した。

　まず、ヒト科ヒト族ヒトが一体の場合を考える。この場合、ヒトは引力に引き寄せられ内部に陥入するが、その頭部を残すところで急激な斥力が働き、安定する(ソガの法則、図1)。

図2　1体問題の一般解

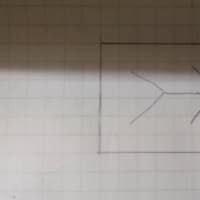
　次に2体の場合を考えると、相互にひかれあい、重力井戸の中でいちゃいちゃ...(図2)

図2　2体問題の特殊解

け　し　か　ら　ん　！

　気を取り直して3体の場合に関して解く。3体以上になると、相互作用は互いとの接触を避ける方向に働き、ヒト対は形成されなくなる(コジマの排他原理)。よって、特殊解は、図3に示す通りとなる。

図3　3体問題の特殊解(1例)

　ヒトが4体になると、ヒトの占有できる軌道はすべて埋まるため、仮定の上では、これ以上人が入ることはない。図4-1が、本レポートでのの目標である、4体問題の特殊解である。また、ここにネコの存在を仮定すると、ネコにはタナカの法則が適用できないので、これらは、引力が釣り合う中心に居座ることになる。よって、図4-2のように、人の配置を何ら変えることなく、モフモフすることになる。これは、ソガティンガー方程式の特異解として表されることが分かっている。