「日記」のブログ記事一覧-gooブログはじめました！

高校情報Ⅰ学習塾・共通テスト対策講座／プログラミング概要とアルゴリズム（フローチャート）/Python・JavaScript

2021-11-24 18:01:19 | 日記

高校情報Ⅰ学習塾・共通テスト対策講座／プログラミング概要とアルゴリズム（フローチャート）/Python・JavaScript

高校情報１　教科書・参考書・問題集・プログラミング・共通テスト

高等学校　情報Ⅰ（情報１）の動画教科書・参考書・問題集です。授業・プログラミング対策/定期試験対策に利用可能！大学入学共通テスト「情報１」対...

【資料ダウンロード】

PDFの他、パワーポイント、学習指導案等の原本も無料提供しています。

情報教育の底上げが目的なので、資料を修正して、学校・塾（営利目的含む）の授業等で利用して頂いて問題ありません。私への連絡不要ですが、利用する際には、YouTubeチャンネル・情報Ⅰ動画教科書・IT用語動画辞典を紹介してもらえると嬉しいです。

■PowerPoint資料
https://toppakou.com/info1/download/30_アルゴリズムとプログラミング/30_アルゴリズムとプログラミング.pptx

■簡易学習指導案
https://toppakou.com/info1/download/30_アルゴリズムとプログラミング/【学習指導案】30_アルゴリズムとプログラミング.docx

【文字おこし】

今回はアルゴリズムとプログラミングの概要について説明していきます。

アルゴリズムとプログラミングの関係について説明していきます。

テストの点数が６０点以上なら合格、そうでなければ不合格と画面に表示したい場合の例で考えていきます。
まず、自分自身の点数を設定します。
そしてその点数が６０点以上か判定します。
当てはまれば合格と表示します。
あてはまならければ不合格と表示します。

このような、問題を解決するための方法や手順をアルゴリズムといいます。

アルゴリズムをコンピュータが実行できる形式であらわしたもの、つまりコンピュータに命令を指示する言語を用いて表したものをプログラムといいます。プログラムは、ソースとやコードなどと言ったりもします。
そして、プログラムを作成することをプログラミングと言います。

このアルゴリズムを視覚的に分かりやすく表現した図をフローチャートといいます。

実際にフローチャートを描きながら記号の説明をしていきます。

画面に
おはよう、こんにちは、おやすみ　と順番に表示するフローチャートを描いていきます。

処理と開始と終了には、このような端子と呼ばれる記号を記述しその中に処理を描いていきます。

まず、おはようと表示する処理はこのような記号を使います。
この記号は、表示で画面に表示されるデータなどを中に記述します。
こんにちは、おやすみも同じように記述します。

―――
今度は、先ほど話題に上げたテストの点数が６０点以上なら合格、それ以外なら不合格とする処理のフローチャートを描いていきます。

先ほどと同じように開始と終了の端子記号の中に処理を記述していきます。

初めの四角は処理を表す記号で演算等の処理を表します。
ｘひだりやじるし０はxという変数の箱に８０を代入しているという意味になります。

次のひし形は判断を表し条件による分岐の記号になります。
中に条件を記述しｘが６０点以上かを判定します。
まず６０点以上の場合の処理を下に記述します。
今回は合格と画面に表示します。

６０点以上でない場合、つまり６０点未満の場合は右から線を出して、ＮＯと記述し不合格を画面表示する処理を描きます。

このままだと、処理が途中で途切れてしまうので、矢印線で合流させます。

―――

今度は繰り返し処理のフローチャートについて説明していきます。

変数x に対して 10 を5 回加算をしながらその都度 x の値を表示する処理のフローチャートを説明していきます。

まずは、文書で処理を説明します。
① x =0　とする。
② i = 1,2,3,4,5とカウントを進めながら以下の処理を行う。
　　xに10を加える。
　　xの値を表示する。

これをフローチャートにしていきます。
先ほどと同じように開始と終了の端子記号の中に処理を記述していきます。
まずは、ｘに０を代入します。

そして、繰り返し処理については、このようなループ端という記号を使います。
繰り返したい処理をこの間に描いていきます。
ループを繰り返す条件をループ記号の上の方に記述します。
今回は変数を1からカウントアップしながら５まで進めるということでiひだりやじるし１２３４５と記述します。
５回繰り返す等と簡略化される場合もあります。

変数ｘに＋１０した値をもう一度ｘに代入するという意味で
ｘひだりやじるしｘ＋１０の処理を記述します。
そして、ｘの値を表示する記号を記述します。

この部分の処理が５回繰り返されます

―――
どんなアルゴリズムでも，処理の流れは，今話した順次，分岐，反復の３つの構造の組み合わせで構成されています。このような処理の流れを制御構造という。

・順次は　1 つ1 つの処理を順番に行うこと
流れ図で表すと、上から下へ記述された順に処理を実行します。。
この図では、処理1 を実行した後に処理2 を実行します。

・分岐は　ある条件に応じて異なる処理を実行することです。
流れ図で表すと、条件により処理を選択する。条件が真のときは処理1 を実行し，偽のときは処理2 を実行するという意味になります。

・反復は、ある条件が満たされている間はその処理を繰り返し実行します。
流れ図で表すと、条件が真の間，処理を繰り返し実行し，偽になるとループ終端の下にある
処理を実行します。

―――

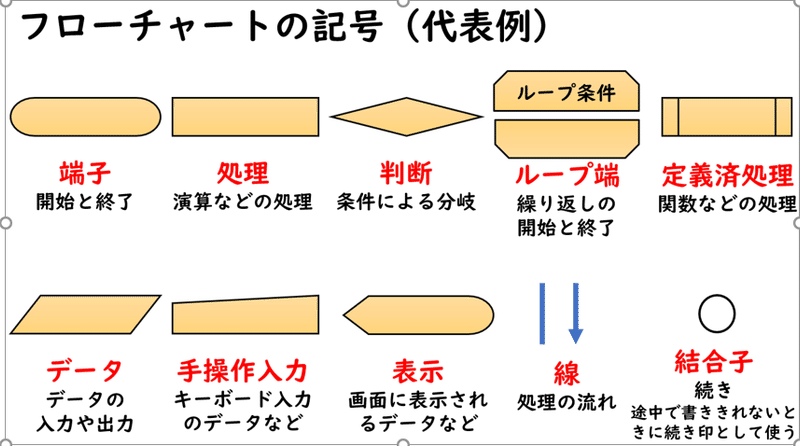
今見てもらったフローチャートで使われる記号は今話したもの以外にも沢山ありますが、
代表的なものを簡単に説明します。

★一覧パワーポイント作成

アルゴリズムを表現する方法は他にもいろいろあります。
今度は給湯ポットの処理を状態遷移図と状態遷移表で表していきます。

給湯ポットにはロック解除ボタンと給湯ボタンがあると仮定します。
状態としては
ロック状態、ロック解除状態、給湯状態があります。
ロック解除状態から再度ロック状態にするには、ロック解除ボタンをもう一度押すか、ロック解除から１分後に自動でロック状態になるものとします。。

はじめの状態を、ロック状態として考えてみます。
まず、ロック解除ボタンを押すと、ロック解除状態となります。

給湯ボタンを押すと　給湯状態となります。
給湯ボタンから手を離すとロック解除状態となります。
そして、１分経過するか　ロック解除ボタンを押すとロック状態となります。

これを、状態遷移表でも表していきます。

まず、ロック解除ボタンはロック状態だったら、ロック解除となり、ロック解除状態だったらロックとなります。給湯状態からの遷移はありません。

１分経過すると、ロック解除状態だったらロックとなります。他の状態からの遷移はありません。

給湯ボタンを押すと、ロック解除状態なら給湯状態となります。
既に給湯状態なら給湯を継続します。
ロック状態だったら、給湯ボタンを押しても何も起こりません

給湯ボタンから手を離すと　給湯中なら給湯停止となります。
他の状態からの遷移はありません。

―――――

今から皆さんが習おうとしている、PythonやJavaScriptやVBAなどは、プログラミング言語やプログラム言語と言われる言語です。
プログラミング言語は、コンピュータに対して動作手順などを適切に指示するために用いられる人工的に構成された言語体系になります。

以前説明しましたが、コンピュータの世界は０と１のビット列を判定します。この０と１のビット列からなる機械語と呼ばれる命令を実行することによって動作します。
ただ、人間にはこの０と１のビット列の機械語を扱うことは難しいために、人間にとって理解しやすい表現で記述できるプログラミング言語が用いられています。

プログラミング言語で記述されたプログラムはコンパイラやインタプリタと呼ばれるソフトウェアで機械語に変換されます。

プログラミング言語には様々な分類方法がありますが、ここでは代表例を説明します。

★分類例　パワーポイント表

――――
プログラミングの工程は、大きく　設計、記述、実行、試験　に分かれます。
設計では先ほどの処理概要やフローチャートのように日本語で行います。
記述はPythonなどのプログラミング言語で行います。
それを、実際にコンピュータ上で動かします。
その実行結果を検証し問題があれば、何が原因かを考え正しい結果が得られるまで同じ手順を繰り返します。
ソフトウェアの不具合（エラー）のことや
プログラムが意図した動きと違う動作をする原因の総称をバグといい、バグを取り除く作業をデバッグと言います。

実行時や結果の検証において様々なエラーが起こります。

たとえばprint(‘こんにちは’)はPythonでこんにちはと表示しなさいの命令ですが、
このようなスペルミスがあった場合、実行時にエラーになります。
このような、文法上のミスによってコンピュータが機械語に変換できないエラーを構文エラーと言います。

また、プログラム実行中に、何らかの誤りが原因でとまることがあります。
たとえば、　変数aに０が代入されていて　100/a　をした場合、実行時に０で割ることができずにエラーとなります。
これを実行時エラーと言います。

プログラム処理が正常終了しても、正しい結果が得られないことがあります。これを論理エラーといいます。

エラーの内容によってプログラムの記述を見直したり、
設計ミスの場合は設計書を修正したあとプログラムを修正する場合もあります。

今回のアルゴリズムとプログラミングの授業は以上になります。
最後までご視聴ありがとうございました。

【解説重要用語】

アルゴリズム、プログラミング、ソース、コード、プログラム、フローチャート、順次、分岐、反復、端子、処理、判断、ループ端、定義済処理、データ、手操作入力、表示、結合子、状態遷移図、状態遷移表、低級言語、高級言語、テキストプログラミング言語、ビジュアルプログラミング言語、コンパイラ型言語、インタプリタ型言語、クライアント型言語、サーバサイド言語、手続き型言語、関数型言語、論理型言語、オブジェクト指向型言語、構文エラー、実行時エラー、論理エラー

★私の目標
「とある男が授業をしてみた」の葉一さん
https://www.youtube.com/user/toaruotokohaichi
※Google社に招待頂いた、「YouTube教育クリエイターサミット2020」で
　葉一さんと文部科学省・Google役員の対談セッションに感銘を受けて、高校情報講座スタートしています。

【参考サイト・参考文献】
文部科学省　「情報Ⅰ」教員研修用教材
https://www.mext.go.jp/a_menu/shotou/zyouhou/detail/1416756.htm

詳細（情Ｉ703　高校情報Ｉ Python）｜情報｜高等学校　教科書・副教材｜実教出版 (jikkyo.co.jp)　検定通過版
https://www.jikkyo.co.jp/book/detail/22023322

令和4年度新版教科書「情報Ⅰ」｜高等学校情報｜日本文教出版 (nichibun-g.co.jp)検定通過版
https://www.nichibun-g.co.jp/textbooks/joho/2022_joho01_1/textbook/

#情報共通テスト #高校情報 #プログラミング言語

高校情報個別指導塾／オブジェクト指向とプログラム設計手法（UML）を徹底解説／共通テスト対策講座／基本情報技術者試験

2021-11-24 17:59:00 | 日記

高校情報個別指導塾／オブジェクト指向とプログラム設計手法（UML）を徹底解説／共通テスト対策講座／基本情報技術者試験

高校情報１　教科書・参考書・問題集・プログラミング・共通テスト

【資料ダウンロード】

PDFの他、パワーポイント、学習指導案等の原本も無料提供しています。

■PowerPoint資料
https://toppakou.com/info1/download/36_A_オブジェクト指向プログラミング/36_A_オブジェクト指向プログラミング.pptx

■簡易学習指導案
https://toppakou.com/info1/download/36_A_オブジェクト指向プログラミング/【学習指導案】36_A_オブジェクト指向プログラミング.docx

【文字おこし】

今回は、オブジェクト指向とプログラムの設計手法について説明していきます。

はじめに１台の車を思い浮かべてみてください。
その車の色は何ですか？
メーカーはどこの車ですか？
車種は普通車ですか？トラックですか？バスですか？

その車にはアクセルやブレーキなどどのような機能がありますか？

ありがとうございます。
私が思い浮かべたのは
メーカーはトヨタ
色は赤
車種は普通車

機能は発進する機能、停止する機能、ハンドル機能です。

私と全く同じ人は少ないと思います。

今話したように一言に車と行っても、色やメーカーや車種などで色んな種類があります。

でも、メーカー、色、車種という属性や発進する、停止する等の処理としては全部の車に共通しますよね。

ということは、メーカー、色、車種はまだ未定だけどそれを入れられる領域と
発進する、停止する等の処理　の車に共通する性質を保持する設計書の様なものがあれば、
皆さんにイメージしてもらったように多種多様な車が簡単に作成できます。

この設計書をもとに生成された車のことをインスタンスやオブジェクトと言います。

オブジェクト指向は、このようにメーカーや色などのデータの属性　と　処理　を一つにまとめた概念になります。
オブジェクトの属性やその値をプロパティと言います。

発進するや停止する等の処理のことをメソッドと言います。

オブジェクトの生成のもととなるオブジェクトの性質を定義した設計書の様なものを、クラスと言います。

車クラスから２台の車オブジェクトを生成していきます。
オブジェクト生成時に名前を決めることができます。
これをオブジェクト名やインスタンス名と言います。
１台目をがっきーの車、２台目をミライの車　というオブジェクト名にします。

１台目のがっきーの車は
メーカー：トヨタ
色：青
車種：普通車
とします。
メソッドは車クラスの発信する機能などがそのまま使えます。

２台目のミライの車は
メーカー：ニッサン
色：オレンジ
車種：普通車
とします。

車クラスから２台の車を作成しましたが、この行為をインスタンス化やオブジェクトの生成と言います。

車種やメーカーなどの属性や発進する、停止するの処理は、カプセルの中に入っているようにひとまとまりになっています。車を使う人にとっては、どのような論理で車が走るのか、停止するのか、データがどんなふうに管理されているのかは必要なく、アクセル踏めば走れば良いですよね。

このように、データとメソッドをオブジェクトに纏めて、オブジェクト内部の状態や構造は隠蔽し、外から見て必要な情報や手続き（処理・メソッド）のみを提供することをカプセル化と言います。

メソッドの呼び出しは、オブジェクト名.メソッド名というように指定すれば呼び出されます。
たとえば、がっきーの車を発進させたければ、がっきーの車.発進する機能　というように呼び出せば、ガッキーの車のオブジェクトだけが発進します。

最高速度の属性を追加してみます。
がっきー車は時速８０キロ、ミライ車は時速２００キロとします。
最高速度で発信というメソッドを呼び出した場合、オブジェクト毎に速度が違うつまり違うふるまいをします。

このように同じメソッドを呼び出しても、オブジェクト毎に振る舞いが異なることを多態性（たたいせい）やポリモーフィズムといいます。

―――
今は１つのクラスで説明しましたが。
クラスには継承という概念があります。
継承とはその名の通り定義されているクラスのプロパティやメソッドを別のクラスに引き継ぐことができます。

たとえば、哺乳類という大きなクラスがあったとします。
哺乳類に共通するプロパティは目の色、毛の色　などがあります。
メソッドとしては食べる、歩く　などがあります。

このクラスを継承して

人間クラスと犬クラスを作ります。
哺乳類クラスのものは引き継げているので、人間だけに存在する　話す　や　仕事するのメソッドを追加することが可能になります。
犬クラスも犬だけで存在するしっぽの太さのプロパティや吠えるなどのメソッドを追加することができます。

上位クラスをスーパークラス、継承先の下位クラスをサブクラスといいます。

このように下位のクラスがもつ共通の特性を抽出して、上位クラスとして定義することを汎化といいます。
逆に、抽象的な上位のクラスをより具体的なクラスとして定義することを特化といいます。
この汎化と特化はis a　関係とも言います。
言い換えると　人間クラス　is a 哺乳類　クラスの関係にあるという意味になります。

――
他には集約と分解と呼ばれるpart of関係というものがあります。

たとえば先ほど車のクラス１つで説明しましたが、車は例えば、エンジンやタイヤやハンドルと言った部品で分解することが可能です。それをそれぞれクラスとして定義することもできます。
つまり下位クラスは上位クラスの一部であるという関係で、下位クラスは上位クラスの性質を分解して定義したものになります。
逆に上位クラスは複数の下位クラスを集約して定義したものになります。

タイヤは車のパーツという意味で
タイヤ　part of 車　から　part of関係と言ったりします。

ここまで、一般的に分かりやすいといわれる入門書などをベースとしたオブジェクト指向の概要を話してきました。
大半の人が、いったい何の役に立つんだ、ただややこしいだけと思っていると思います。
私自身、長年オブジェクト指向を利用した大規模システム設計に携わっていました。
実際に設計に携わる中でオブジェクト指向の凄さというのを体験しました。
実際の業務でどのようなイメージで設計していたかを簡単に説明します。

■
たとえば皆さんが持っているスマートフォンは家電量販店やauやNTTドコモやソフトバンクの様なショップで購入したと思います。

このような携帯電話会社の場合どのようなクラスが必要か考えてみましょう。

まず、契約者に関する情報が必要なので契約者クラスとします。
氏名や生年月日などが存在します。

そして、スマートフォンの端末クラスが存在します。
機種や機器固有の製造番号が存在します。

携帯電話には料金プランやオプションサービスが存在します。
それをサービスクラスとし、サービスの種類が存在します。

たとえば、太郎君がスマートフォンを購入した場合
契約者クラスから太郎君用のオブジェクトが生成され氏名に太郎、太郎君の生年月日が設定されます。
端末オブジェクトに太郎君の買った機種、製造番号、そして加入したサービスの分、サービスオブジェクトが作られます。

花子さんが同じタイミングでスマートフォンを購入した場合も、同様に花子さん用のオブジェクトが生成されます。
多くの場合、オブジェクトに設定されたプロパティ情報はデータベースに登録されます。
数年経過し太郎君が機種変更をしたい場合は、データベースからデータを取得し、太郎君のオブジェクトを再生成し、端末オブジェクトの情報を書き換えたりします。

今は太郎君と花子さん２名の話でしたが、スマートフォンのユーザは数千万人になります。
数千万人の場合でも、契約者クラスも端末クラスもサービスクラスも１つだけで済みます。

このオブジェクト指向はシステム開発の効率化や役割分担の明確化という面でも役に立ちます。
以前、IT業界の真実の動画でも話しましたが、携帯電話会社の様な大規模システム開発の場合は、数百社のシステム会社が多重構造でかかわっています。

契約者クラスはA社とその協力会社担当
端末クラスはB社とその協力会社担当　と言ったように　機能実装の役割分担がやりやすいメリットがあります。
また、システムトラブルのニュースをよく耳にすると思いますが、世の中にリリースした後もシステムにはトラブルがつきものです。
トラブルは０にするのは難しく、トラブルが起こった場合、いかに早く、迅速に対応するかという運用体制の構築が重要になってきます。

このように役割分担しておけば、仮に端末クラスの機能でエラーが発生した場合
まずはB社に調査してもらうことができます。
調査次第では必要に応じて、他の契約者クラスやサービスクラスの会社にB社から調査依頼したりします。

システム業界＝プログラミング＝１人で黙々と行うイメージがある人も多いと思いますが、
ある程度のシステム規模の開発は、打合せも多くチームワークが何よりも重要になってきます。

――――――――――――

次にプログラムの設計手法の概要について説明します。
システム開発では、PythonやJavaScriptなどのプログラミング言語でプログラミングを行う前には、プログラムの流れなどを説明した設計が行われます。
そのアルゴリズムの記述には以前説明したフローチャートや状態遷移図や状態遷移表などがよく使われます。
しかし、複数の処理を同時に実行したり、ユーザの操作に応じて処理を実行したりする複雑な処理を表現するには必ずしも適しているとは言えません。

このような場合にUMLという統一モデリング言語が使われることが多いです。
UMLはデータの構造や処理の流れなどソフトウェアに関連する様々な設計や機能を図示するための表記を定めたものです。
UMLで規定されている図をダイアグラムといい、全部で１３種類あります。
ただ、１３種類全部使っているシステム開発現場は私自身は見たことはありません。
そのシステム開発プロジェクトに適したものを取捨選択しています。

概要だけになりますが、１３種類を簡単に説明します。
UMLは、大きく　構造を表す構造図とふるまいを表すふるまい図にわかれます。

構造図は
　クラス図、オブジェクト図、パッケージ図、コンポーネント図、複合構造図、配置図　があります。

クラス図は、クラスの定義や関連付けなどクラス構造を表します。

オブジェクト図は、クラスを実体化させるインスタンスの具体的な関係をあらわします。

パッケージ図は、クラスなどがどのようにグループ化されているかをあらわします。

コンポーネント図は　処理を構成する複数のクラスを１つのコンポーネントとみなし、その内部構造と相互の関係をあらわします。

複合構造図は、複数クラスを内包するクラスやコンポーネントの内部構造をあらわします。

配置図は、システムを構成する物理的な構造をあらわします。

次に振る舞い図は、
ユースケース図
アクティビティ図
状態遷移図
シーケンス図
コミュニケーション図
相互作用概要図
タイミング図　があります。

ユースケース図は、システムの利用者や外部システムからの要求に対して、システムがどのようにふるまいをするかを表します。
アクティビティ図は、システム実行時における、一連の処理の流れや状態遷移を表します。フローチャートと同じようなものと考えてください。
状態遷移図は、イベントによっておこる、オブジェクトの状態遷移を表します。
シーケンス図は、オブジェクト間のやり取りを、時系列に沿って表します。私の経験上、このシーケンス図はほとんどのシステム開発プロジェクトで利用していました。
コミュニケーション図は、オブジェクト間の関連と、そこで行われるメッセージのやり取りを表します。
相互作用概要図はユースケース図やシーケンス図などを構成要素として、より大枠の処理の流れを表します。
タイミング図はオブジェクトの状態遷移を時系列で表します。

今回のオブジェクト指向とプログラム設計についての授業は以上になります。
最後までご視聴ありがとうございました。

【解説重要用語】

インスタンス、オブジェクト、オブジェクト指向、プロパティ、クラス、メソッド、カプセル化、メッセージ、多態性・ポリモーフィズム、クラスの継承、is-a関係、汎化・特化、集約と分解、part of関係クラス図、オブジェクト図、パッケージ図、コンポーネント図、複合構造図（コポジット構造図）、配置図、ユースケース図、アクティビティ図、状態遷移図（状態マシン図）、シーケンス図、コミュニケーション図、相互作用概要図、タイミング図、UML（統一モデリング言語）

【参考サイト・参考文献】
文部科学省　「情報Ⅰ」教員研修用教材
https://www.mext.go.jp/a_menu/shotou/zyouhou/detail/1416756.htm

詳細（情Ｉ703　高校情報Ｉ Python）｜情報｜高等学校　教科書・副教材｜実教出版 (jikkyo.co.jp)　検定通過版
https://www.jikkyo.co.jp/book/detail/22023322

令和4年度新版教科書「情報Ⅰ」｜高等学校情報｜日本文教出版 (nichibun-g.co.jp)検定通過版
https://www.nichibun-g.co.jp/textbooks/joho/2022_joho01_1/textbook/

#プログラム設計手法 #高校情報 #オブジェクト指向

【高校情報共通テスト対策／学習塾／個別指導】モンテカルロ法（円周率）、確率的・確定的モデル、シミュレーション、物理・論理モデル／教科書完全準拠授業動画

2021-11-20 22:10:10 | 日記

【高校情報Ⅰ参考書・共通テスト】モンテカルロ法（円周率）、確率的・確定的モデル、シミュレーション、物理・論理モデル／教科書完全準拠授業動画

高校情報１　教科書・参考書・問題集・プログラミング・共通テスト

【資料ダウンロード】

PDFの他、パワーポイント、学習指導案等の原本も無料提供しています。

■PowerPoint資料
https://toppakou.com/info1/download/29_モデル化とシミュレーション/29_モデル化とシミュレーション.pptx

■Excel資料
https://toppakou.com/info1/download/29_モデル化とシミュレーション/29_モデル化とシミュレーション.xlsx

■簡易学習指導案
https://toppakou.com/info1/download/29_モデル化とシミュレーション/【学習指導案】29_モデル化とシミュレーション.docx

【文字おこし】

今回は様々なモデルの種類、モンテカルロ法、シミュレーションについて説明していきます。

事物や現象の本質的な形状や法則性を抽象化して，より単純化したものを「モデル」といいます。
そして、事物や現象のモデルを作ることをモデル化といいます。

このモデルを使って、実際には行う事が困難な実験を計算だけで行なったり，複雑
な現象を再現したりするための手段としても活用できたりします。

また、このような問題解決の結果を予測するために同様の条件で模擬動作させてみることをシミュレーションと言います。

モデルにはいくつも種類があります。
今回は代表的なものについて説明していきます。

■物理モデルと論理モデル
物理モデルと論理モデルについて説明していきます。
物理モデルは　実物を模したモデルのことです。
　物理モデルの中でも何種類かあり、例えば、モデルルームの様な実物と同じ形をした実物モデル、　実際より小さく作られたミニカーなどの縮尺モデル、　逆に実際より大きく作成された分子模型などの拡大モデルなどがあります。

論理モデルは　現象や手続きなどを表現したモデルになります。
　論理モデルの中でも何種類かあり、例えば、減少や法則などを数学的に表した数式モデル、
　バスや列車の路線図やトーナメント表などの図的モデルなどがあります。

■静的モデルと動的モデル
次に、静的モデルと動的モデルについて説明していきます。
静的モデルは　時間の経過が他の要素に影響を与えないモデルになります。
　たとえば、　円の半径が分かれば半径の２乗×円周率で円の面積が求められますが、その円の半径と面積の関係などがあげられます。

動的モデルは　時間の経過が他の要素に影響を与えるモデルのことで、
確定的モデルと確率的モデルに分けられます。

■確定的モデルと確率的モデル
確定的モデルは、変動する要素がなく、結果が一つに定まるモデルになります。

たとえば、時速６０キロの車が常に同じ速度で走り続けた場合、１時間で６０キロメートル　２時間で１２０キロメートル、３時間で１８０キロメートルと時間と移動距離が予測できます。

確率的モデルは、変動する要素があり結果が１つにならないモデルになります。
たとえばサイコロを振って出る目はランダムな値になります。
この確率的モデルの中で、ランダムな数である乱数を用いて問題解決する手法にモンテカルロ法があります。

■モンテカルロ法
モンテカルロ法の特徴は対象のモデルに乱数を大量に生成して入力し，近似解を得ようとする手法になります。

分かりずらいと思うので、円周率の例で説明していきます。

まず、円周率は円の直径に対する円周の長さの比率のことになります。
そして、円の面積は　円周率×半径の２乗　になります。
公式で表すと円の面積をS　半径をｒ　円周率をπとした場合
Ｓ＝πｒ２乗になります。

なので、半径を１とした場合　π×１×１＝πとなり。
円周率と円の面積とがイコールになります。

円の中心をX軸　Y軸共に０とした場合
円の上の部分は　Xは０　Yは１　円の右側は　Xは１　Yは０となります。
右斜め上はXは１　Yも１　となります。

その４点を結ぶと、長さが１の正方形が描けます。

つぎに、その正方形の中にランダムに点を打っていきます。
通常はもっと多くの点を打ちますが、分かりやすくするために２０個ランダムに点を打ちます。

その打った点について、円の内部に存在する点を数えます。

今回は２０個のうち　１５個が円の内側に入ったとします。

正方形の面積は１×１で１になります。

その面積に対して、均等に点が打たれたとした場合、
円の面積は　２０分の１５で表されます。

つまり、正方形全体に対する、円の内部の点の割合を円の面積として考えるという意味になります。

今回は円全体に対する面積の４分の１の面積を求めました。
つまり、これを４倍すれば円全体の面積となります。

そして、はじめに話したように、半径１の円の面積が円周率と一致するので
今回の場合は
２０分の１５　×４　が円周率となります。

このランダムに打たれる点の数を増やすほど、精度が上がり、皆が知っている３．１４１５の円周率に近づいていきます。

点が円の内部にあるかどうかは、置いた点のｘとｙの座標を確認して
ｘの２乗プラスｙの２乗の値が１より小さければ、円の内側に点があります。
つまりｘの２乗プラスｙの２乗が１の場合は点が円周上に位置しているということになります。

★確定的モデルのシミュレーション

確定的モデルの簡単なシミュレーションをエクセルを使って行っていきます。

お風呂に水を入れるときに、水を入れた時間と湯船にたまる水の量の関係を表すモデルを作成していきます。

１分当たりに何リットルの水が溜まるかの　水の流入速度
何分ごとに水量を取得するかの　時間間隔　は任意の値を入力できるようにします。

シミュレーションの表は
経過時間と水量の列があり初めの行は０とします。
次の経過時間は時間間隔によって変わってくるので、前のセルの値と時間間隔を合算します。オートフィルを使って数式を下にコピーできるようにするためには、時間間隔の行はずらしたらいけないので、時間間隔の行番号の前にドルマークを付けて絶対参照にします。
オートフィルを使って下に数式をコピーします。時間間隔のセルの値を変更すると、経過時間の間隔も変更されます。

次の水量は経過時間と流入速度に比例するのでそれを掛け合わせます。

これも数式を下にコピーできるようにするために、流入速度の行をずらさないように、流入速度の行番号の前にドルマークを付けて絶対参照にします。
オートフィルを使って下に数式をコピーします。流入速度のセルの値を変更すると、水量の値も変更されます。

今日のモデル化とシミュレーションの授業は以上になります。
最後までご視聴ありがとうございました。

【解説重要用語】

モデル化、シミュレーション、物理モデル、実物モデル、縮尺モデル、拡大モデル、論理モデル、数式モデル、図的モデル、静的モデル、動的モデル、確定的モデル、確率的モデル、円周率、モンテカルロ法

【参考サイト・参考文献】
路線・駅の情報 | 東京メトロ (tokyometro.jp)　：路線図転載
https://www.tokyometro.jp/station/

文部科学省　「情報Ⅰ」教員研修用教材
https://www.mext.go.jp/a_menu/shotou/zyouhou/detail/1416756.htm

詳細（情Ｉ703　高校情報Ｉ Python）｜情報｜高等学校　教科書・副教材｜実教出版 (jikkyo.co.jp)　検定通過版
https://www.jikkyo.co.jp/book/detail/22023322

令和4年度新版教科書「情報Ⅰ」｜高等学校情報｜日本文教出版 (nichibun-g.co.jp)検定通過版
https://www.nichibun-g.co.jp/textbooks/joho/2022_joho01_1/textbook/

【高校情報共通テスト対策／学習塾／個別指導】区間推定・χ２乗検定（カイ二乗検定）・クロス集計・９５％信頼区間教科書準拠

2021-11-20 22:09:09 | 日記

【高校情報Ⅰ学習塾・共通テスト】区間推定・χ２乗検定（カイ二乗検定）・クロス集計・９５％信頼区間教科書準拠

高校情報１　教科書・参考書・問題集・プログラミング・共通テスト

【資料ダウンロード】

PDFの他、パワーポイント、学習指導案等の原本も無料提供しています。

■PowerPoint資料
https://toppakou.com/info1/download/28ADVANCE区間推定とクロス集計/28ADVANCE区間推定とクロス集計.pptx

■Excel資料
https://toppakou.com/info1/download/28ADVANCE区間推定とクロス集計/28ADVANCE区間推定とクロス集計.xlsx

■簡易学習指導案
https://toppakou.com/info1/download/28ADVANCE区間推定とクロス集計/【学習指導案】28ADVANCE区間推定とクロス集計.docx

【文字おこし】

今回は、区間推定、クロス集計、χ（かい）二乗検定について説明していきます。
事前知識として、以前動画解説した母集団と標本とZ検定、ｔ検定についての知識が必要になります。

知識習得が未だの方は概要欄に貼ってあるURLから先に確認頂けると幸いです。

以前、母集団と標本の説明の中で　１０万個のどらやきの母集団の中から、１００個のどら焼きを無作為に抽出する話をしました。

無作為に抽出しても、母平均と標本平均には誤差が発生する可能性があります。
また、１回目の抽出は平均１０１ｇ　２回目は９９ｇと言ったように標本内でも取得するたびに差が出る可能性があります。

標本をもとにして調査し確率的に母集団がどのような値を持っているかを推測することを、推定と言います。
テキスト的な表現だと、「標本における一定の法則を母集団に当てはめて推し量る」ことを推定といいます。
推定には、母平均μ＝１００と言ったように１点で表す　点推定や
９５≦μ≦105　と言ったように推定値に一定の幅を持たせる区間推定があります。

今回は区間推定について掘り下げて説明していきます。

先ほど、標本平均にも誤差が発生すると話しましたが、何度も母集団から抽出しその平均値の発生頻度を調べると標本平均も正規分布となります。

区間推定では、この正規分布の９５％に属する範囲は高い確率で信頼できるとして、その範囲を９５％信頼区間と言います。

Z値になおすと、両端２．５％の位置は１．９６でそれを基準に内側に属する区間になります。

具体的な数式で説明します。
母分散が分かっている場合と分かっていない場合で分かれます。

数式だけだと分かりずらいと思うので具体的な数値を当てはめながら練習問題を解いて行きましょう。
――
★練習問題
母集団の母分散は２５．０ということが分かっている。
この母集団から１００個を標本として無作為に抽出したところ、標本平均は８．６０であった。
母平均μの９５％信頼区間を求めてください。

★パワポ参照

つぎはクロス集計とΧ（かい）２乗検定について説明していきます。

とある高校の１年生と２年生を対象に、学校の校則変更に賛成か反対かのアンケートを取った結果です。
この高校では１年生が２２０人　２年生が１８０人です。
１年生で賛成は１７５人　反対は４５人
２年生で賛成は１２５人　反対は５５人　でした。

賛成の合計は３００人　反対の合計は１００人になります。
　　１年生と２年生の合計人数は４００人になります。

この表をクロス表と言い、このような集計作業をクロス集計と言います。

この結果から　１年生と２年生の回答に有意な差があるといえるかを調べる仮説検定方法にカイ２乗検定があります。χの記号はエックスのように見えますが、χ　かい　と読みます。パソコンで　かい　と入力しても候補として出てきます。

仮説検定なので帰無仮説と立証したい対立仮説が必要になります。

帰無仮説は、１年生と２年生で有意な差は無い
対立仮説は　１年生と２年生で有意な差がある　とします。

χ二乗検定を行う上で期待度数という知識が必要になってきます。

期待度数は、アンケート結果の合計が分かっている状態で、全体の割合から考えて期待される数になります。

たとえば１年生で賛成の人の期待度数は　賛成の合計３００×１年生の合計人数２２０÷全体人数の４００　を計算すると１６５になります。
１年生で反対の人の期待度数は　反対の合計１００×１年生の合計人数２２０÷全体人数の４００　を計算すると５５になります。
２年生も同様に計算すると１３５と４５になります。

χ２乗検定のχ２乗値は　（実測度数―期待度数）　の２乗　÷　期待度数　の値を合計になります。

この式からわかることは・・
• 期待度数と観測度数が完全に一致すれば、χ２乗値はゼロになる
• 逆に、不一致（ずれ）が大きくなれば、χ２乗値は大きな値になる

期待度数に実測度数がどの程度一致しているか調べる検定を適合度検定と言い
　χ二乗検定も適合度検定の１つになります。

１年生の賛成のセルについては　（１７５―１６５）の２乗　÷　１６５の式で計算すると、小数第５位を四捨五入して０．６０６０　となります。

他のセルも同様に計算していき　値を合計したχ２乗値は　5.3869となります。

ここで求めたχ２乗値が今までのｔ値やＺ値に相当するものと思ってください。
有意水準５％のχ２乗分布表はこちらになります。

ここの自由度について説明していきます。
自由度は自由に決められるあたいの数ことで
たとえばこのクロス集計表で合計が既に決まっている状態の表の場合、１つのセルに値を入れると他のセルの値はきまります。
左上に２００をいれると　その右側は合計の２２０―２００で２０となります。
下がわは３００―２００で１００となります。そのとなりは１８０―１００で８０となります。
なので自由に決められる値は１つだけで自由度は１になります。
セルの数が増えるほど自由度は増えますが
（行数―１）×（列数―１）　で簡単に求めることができます。
今回は行数は２　列数も２　なので　計算すると１になり　先ほど説明した数と一致しました。

今回は自由度１なのでχ二乗分布表では限界値は３．８４１となります。
今回求めたχ２乗値の５．３８６９は限界値を上回っているので、帰無仮説を棄却し、１年生と２年生で有意な差があるということになります。

――
今話した計算はエクセルを使って簡単に実施することが可能です
まず右上の期待度数は賛成の合計×１年生の合計／全体合計　で各セルを指定します。
オートフィルを使ってコピーできるようにドルマークを付けて絶対参照にしていきましょう。
賛成の合計は、行は固定なので行の前にドルマークを付けます。
F4キーを何度か押してドルマークの位置を変更できます。
学年の合計は列は固定なので、列の前にドルマークを付けます。
全体合計は列も行も固定なので、すべてにドルマークを付けます。
オートフィルを使ってコピーすると期待度数がすべて埋められました。

次にｐ値を求めていきます。
この結果になる確率になります。これはＣＨＩＴＥＳＴ（カイテスト）関数を使います。
第一引数に実測度数を範囲指定します。
第二引数に期待度数を範囲指定します。
Ｐ値が算出されました。約２％の確率で起こる結果になります。
次にχ２乗値を求めます。これはＣＨＩＩＮＶ（カイ・インバース）関数を使います。
第一引数に先ほど求めたｐ値、第二引数に自由度をしていすると、χ２乗値が算出されます。

今日の区間推定、クロス集計、χ２乗検定の説明は以上になります。
最後までご視聴ありがとうございました。

【解説重要用語】

区間推定、９５％信頼区間、クロス集計、クロス表、χ二乗検定（カイにじょうけんてい）、期待度数、実測度数、χ二乗値、適合度検定、χ二乗分布表、χ二乗検定の自由度、

【参考サイト・参考文献】
数学嫌いのための社会統計学〔第2版〕
https://www.amazon.co.jp/s?k=%E7%B5%B1%E8%A8%88%E5%AD%A6+%E6%95%B0%E5%AD%A6%E5%AB%8C%E3%81%84&ref=nb_sb_noss
※佛教大学　情報科教員養成　基礎統計学のテキスト

予備校のノリで学ぶ「大学の数学・物理」 - YouTube
https://www.youtube.com/channel/UCqmWJJolqAgjIdLqK3zD1QQ

文部科学省　「情報Ⅰ」教員研修用教材
https://www.mext.go.jp/a_menu/shotou/zyouhou/detail/1416756.htm

詳細（情Ｉ703　高校情報Ｉ Python）｜情報｜高等学校　教科書・副教材｜実教出版 (jikkyo.co.jp)　検定通過版
https://www.jikkyo.co.jp/book/detail/22023322

令和4年度新版教科書「情報Ⅰ」｜高等学校情報｜日本文教出版 (nichibun-g.co.jp)検定通過版
https://www.nichibun-g.co.jp/textbooks/joho/2022_joho01_1/textbook/

#区間推定 #高校情報 #統計学

【高校情報共通テスト対策／学習塾／個別指導】相関係数（共分散・偏差積和・最小二乗法）・回帰直線・散布図・時系列分析（移動平均法）についての授業【高校情報Ⅰ大学入学共通テスト】教科書準拠問題集

2021-11-20 22:08:08 | 日記

相関係数（共分散・偏差積和・最小二乗法）・回帰直線・散布図・時系列分析（移動平均法）についての授業【高校情報Ⅰ大学入学共通テスト】教科書準拠問題集

高校情報１　教科書・参考書・問題集・プログラミング・共通テスト

【資料ダウンロード】

PDFの他、パワーポイント、学習指導案等の原本も無料提供しています。

■PowerPoint資料
https://toppakou.com/info1/download/28_時系列分析と回帰分析/28_時系列分析と回帰分析.pptx

■Excel資料
https://toppakou.com/info1/download/28_時系列分析と回帰分析/28_時系列分析と回帰分析.xlsx

■簡易学習指導案
https://toppakou.com/info1/download/28_時系列分析と回帰分析/【学習指導案】28_時系列分析と回帰分析.docx

【文字おこし】

今回は、回帰分析関連の散布図、相関係数、回帰式、最小二乗法そして時系列分析について説明していきます。

これはとあるクラスの情報と数学の試験の点数を情報の点数が低い順に並び替えた表です。
表を見ると何となく、情報の点数が低い人は数学の点数も低い
逆に情報の点数が高い人は数学の点数も高い傾向がある感じがします。
しかし、Dさんのように情報の点数が高くても数学がそれほど高くない場合もあります。

視覚的にその関係性が判断できる散布図というグラフがあります。

横軸Xを情報の点数とします。縦軸Yを数学の点数とします。

情報が５５点　数学が５７点のAさんは、この位置に点を描きます。
同じように他の人も点を打っていきます。

点が右肩上がりになっていることが分かります。

この散布図が右肩上がりの場合は、情報の点数が高ければ数学も点数が高いという、正の関連があります。これを正の相関といいます。
一方散布図が右肩下がりの場合、具体的には情報の点数が高ければ数学の点数は低いという負の関連があります。これを負の相関といいます。

関連には強弱があります。関連が強いほど散布図の点が線上になっていきます。
関連が弱い、又は関連が無いほど散布図の点はまばらになっていきます。

この点数や身長、体重の様な、人や集団によって異なる能力や性質のことを変数と言います。
散布図は教科書的な説明では、二つの連続変数の関連性をグラフで示したものになります。
点の散らばり具合で、２変数の関連性を視覚的に把握するために用いられます。

相関が強い場合は散布図は視覚的に相関関係が分かりやすいですが、例えばこの図の場合、右肩上がりのようには見えますが、相関が無いものと大きな違いが見いだせない人もいる可能性もあります。

そこで散布図での関連性を具体的な数値で判断できるものとして、相関係数というものが使われます。

相関係数はふたつの連続変数の直線的関連性の強さと方向性を示す数値のことになります。

今回の情報の点数を変数X、数学の点数を変数Yとすると、
相関係数はｒXYと表し、―１から＋１までの値をとります。
相関係数ｒｘｙ＝１は　完全な正の相関で、右肩上がり一直線上に並びます。
そして相関係数ｒｘｙ＝―１は完全な負の相関で　右肩下がりの一直線上にならびます。
相関係数ｒｘｙ＝０は無相関になります。

０に近づくほど、散布図からは相関関係が読み取りずらくなってきます。

――
相関関係の強さの世間相場は比較対象などによって違いがあります。
一つの目安として、プラスマイナス０．７を上回れば　比較的強い相関と言われることがあります。
プラスマイナス０．４～０．７までは中程度の相関　それ以下は、弱い相関で散布図上では相関を読み取るのは難しくなります。

今話した目安を示すのが難しい理由について、例えば、心理系の研究が扱う個々人のデータは一般的にあまり強い相関は観察されないことから＋－０．４～＋―０．７の相関でも強いと評価できることが多いです。
しかし、地域別の集計データや理科系の実験データは比較的高い相関が観測されることから＋－０．４～＋―０．７でも弱いと判断されることがあります
このような理由で、相関関係の強さの世間相場は比較対象などによって差が出てきます。

―――
　
今説明した相関係数をどのように求めるか説明していきます。
計算はいくつかの工程が必要で若干ややこしいので、別にエクセルを使って導き出す方法も後ほど説明します。
先に、計算過程の概要を実際に数値を当てはめながら説明していきます。

大きく３つのステップに分かれます。
STEP1は　偏差積和の計算
STEP2は共分散の計算
STEP3は　共分散を標準偏差の積で割り相関係数を求める
という流れです。

サンプルデータとして正の相関がある、情報と数学のテストの結果５人分を使います。
簡単にするため敢えて人数は少なくしています。

まず偏差積和の計算を行います。
偏差は値と平均点との差になります。

情報の平均点は７２点なので、Aさんの情報の偏差は５５－７２　でー１７になります。
数学の平均点は７３点なので、Aさんの数学の偏差は５７－７３でー１６になります。
それぞれの人の情報と数学の偏差を求めます。

次に各個人の求めた情報と数学偏差を掛け合わせます。
たとえばAさんの場合は-17×-16で272となります。

次にその求めた偏差の積を全て足し合わせると６８６になります。
これが偏差積和になります。

―――

次に共分散の計算を行います。
共分散の計算は簡単で先ほど求めた、情報と数学の偏差積和をデータの個数で割ってあげます。
偏差積和の特性上、データの個数が増すと、関連の強さとは無関係に絶対値が大きくなります。
そのため、データの個数で割って調整をします。
この値を共分散と言います。

データ個数は情報と数学を１セットとして考えてください。
今回は　データ個数は５なので　５分の　偏差積和　６８６　で
計算結果は１３７．２となります。

纏めると共分散は偏差積和をN　つまりデータの個数で割ったものになります。。
そしてこの共分散は相関係数の計算や後ほど説明する回帰分析で使われる値になります。

――
次に求めた共分散をもとにして相関係数を求めます。

共分散は、測定する単位によって値が大きく変わってきてしまうデメリットがあります。
たとえば今は１００点満点のテストの話で進めていますが、テストが１０点満点だと値が小さくなります。逆に２００点満点のテストだと値が大きくなり、お互いの相関を比べることは困難になります。

そこで、先ほど話したー１から１までの共通の尺度である相関係数にしていきます。

相関係数は情報と数学それぞれの標準偏差が必要になります。
以前説明した方法で標準偏差を求めると
情報の標準偏差　は１３．４
数学の標準偏差　は１１．８　になります。

情報の標準偏差×数学の標準偏差　分の　先ほど求めた共分散　で相関係数を求めることができます。

計算すると０．８７になり　これが相関係数になります。

★★エクセル解説
共分散や相関係数はExcel関数で簡単に求めることができます。
共分散はCOVARIANCE.P(コバリアンスドット　ピー)関数を使用します。
第一引数に情報の点数を範囲指定します。
第二引数に数学の点数を範囲指定します。
先ほど地道に計算した共分散が算出されました。

相関係数は、CORREL(コリレーション・コエフィシェント)関数を利用します。
第一引数に情報の点数を範囲指定します。
第二引数に数学の点数を範囲指定します。
先ほど地道に計算した相関係数が算出されました。

―――

今説明した散布図の点の分布を貫く一本の直線を実際に描き、それを表現する数式を求めれば、一方の変数の値から他方の変数値を予想することが可能になります。
たとえば、数学と情報の試験結果に強い相関がある場合　数学が５０点の場合　情報が何点かということがある程度予想可能になります。

この散布図の点の分布をつらぬく直線を回帰直線と言います。そして回帰直線を表現する数式を回帰式と呼びます。
また、Xの値でYの値を予測する場合。
Xを独立変数。　Yを従属変数と呼びます。

回帰直線の数式は一般的に　Y＝aX+bという形になります。
aは回帰係数といい、回帰直線の傾きを意味します。
bは切片といい、Xが０の時のYの値を意味します。

では、回帰直線はどのように描けばよいでしょうか。
自由に直線引いたら人によって変わってしまう可能性があります。
回帰直線は一定のルールが決まっており、最も一般的なルールは最小二乗法になります。
この図のように、上手く回帰直線を引いても、各点と回帰直線との間にはズレが出てきます。
最小２乗法は、回帰直線を各点とのＹ軸方向のずれがトータルで最も小さくなるように描く手法になります。
教科書的な表現では、誤差の２乗を合計した値が最小になるように回帰式のaとbを求めることになります。
２乗する理由は＋と－を合計すると相殺されてしまうため、それを防ぐためにプラスの値で出るように２乗しています。

先ほど共分散を求めた情報と数学の５人の試験結果の回帰直線式を求めていきます。

手順は３ステップで
Ｓｔｅｐ１は回帰係数aを求める
Ｓｔｅｐ２は切片bをもとめて回帰式を完成させる
Ｓｔｅｐ３は回帰直線を描くことです。

それぞれについて説明していきます。

まず回帰係数aは　独立変数Ｘの分散　分の　独立変数Ｘと従属変数Ｙの共分散　になります。
つまり、情報の分散　分の　先ほど求めた情報と数学の共分散になります。

これに当てはめると　０.７６３９となります。

そして切片bは従属変数Ｙの数学の平均値　―　（先ほど求めた）回帰係数a×独立変数Ｘの情報の平均値になります。

数学の平均点は７３　―　回帰係数は０．７６３９　×　情報の平均点７２
を計算すると１７．９９９２となります。

求めた値を回帰式に当てはめると　
Y＝0.7639X+17.9992　となります。

これで回帰式が完成したので　後は任意の２点を決めてそれを定規で結べば回帰直線が出来上がります。

たとえば、Ｘが０のときはＹは17.9992　Ｘが５０の時はＹは５６．１９４２となり、それの点を結ぶと回帰直線が描けます。

★★エクセル解説
回帰直線はエクセルのグラフ機能で簡単に描くことができます。
まずは散布図は情報と数学の点数を範囲指定し、グラフの指定で散布図を選ぶと簡単にグラフが作成されます。

どれか１つの点の上で右クリックし、近似曲線の追加を選択します。
線形近似を選択し下の方にあるグラフに数式を表示するを選ぶと先ほどの回帰式が自動計算されて表示されます。
グラフにR2乗値を表示するにチェックして表示される値は回帰直線・回帰式の当てはまりの良さを０～１の数字で表したもので、決定係数といいます。高校情報の教科書ではここまでは言及していないので詳しい説明は割愛します。

―――

気温の変化のように　、時間と共に変動する量を時間順に並べたものを時系列データと言います。
この時系列データを分析することで、全体的な傾向を捉えたり、将来の動きを予測することができます。
時系列データの傾向を調べる方法として、細かな変動を取り除いて主な動きを明らかにするための平滑化などの方法があります。

一定時間範囲のデータの平均値をその範囲の代表値とする方法である、移動平均法について説明していきます。。

この表はある都市の２０００年から２０２０年の各年の平均気温です。

１年ごとなので折れ線グラフはギザギザしています。

５年間を１つの単位とする移動平均を求めていきます。
アベレージ関数を使って２０００年から２００４年の移動平均を求めます。
次に２００１年から２００５年の移動平均を求めます。
オートフィルを使うと５年単位の平均の範囲も１年ずつ移動してくれるので便利です。

求めた移動平均も含めて折れ線グラフで表示します。

線が滑らかになり、気温が上昇傾向にあることが分かりやすくなりました。

今回の授業は以上になります。最後までご視聴ありがとうございました。

【解説重要用語】

散布図、正の相関、負の相関、相関係数、偏差積和、共分散、回帰分析、回帰式、最小二乗法、時系列データ、移動平均法、時系列分析

予備校のノリで学ぶ「大学の数学・物理」 - YouTube
https://www.youtube.com/channel/UCqmWJJolqAgjIdLqK3zD1QQ

文部科学省　「情報Ⅰ」教員研修用教材
https://www.mext.go.jp/a_menu/shotou/zyouhou/detail/1416756.htm

詳細（情Ｉ703　高校情報Ｉ Python）｜情報｜高等学校　教科書・副教材｜実教出版 (jikkyo.co.jp)　検定通過版
https://www.jikkyo.co.jp/book/detail/22023322

令和4年度新版教科書「情報Ⅰ」｜高等学校情報｜日本文教出版 (nichibun-g.co.jp)検定通過版
https://www.nichibun-g.co.jp/textbooks/joho/2022_joho01_1/textbook/

goo blog お知らせ

	ブログを読むだけ。毎月の訪問日数に応じてポイント進呈
	【コメント募集中】「物々交換」したことはありますか？
	gooブロガーの今日のひとこと
	訪問者数に応じてdポイント最大1,000pt当たる！