【高校情報Ⅰ学習塾・共通テスト】母集団と標本/仮説検定(Z検定とt検定)/帰無仮説・有意水準、自由度、t分布、両側検定・片側検定について解説/統計学

高校情報1 教科書・参考書・問題集・プログラミング・共通テスト
高等学校 情報Ⅰ(情報1)の動画教科書・参考書・問題集です。授業・プログラミング対策/定期試験対策に利用可能!大学入学共通テスト「情報1」対...
【資料ダウンロード】
PDFの他、パワーポイント、学習指導案 等の原本も無料提供しています。
情報教育の底上げが目的なので、資料を修正して、学校・塾(営利目的含む)の授業等で利用して頂いて問題ありません。私への連絡不要ですが、利用する際には、YouTubeチャンネル・情報Ⅰ動画教科書・IT用語動画辞典を紹介してもらえると嬉しいです。
■PowerPoint資料
https://toppakou.com/info1/download/27_ADVANCE_母集団と標本・仮説検定/27A_02_母集団と標本/仮説検定.pptx
■簡易学習指導案
https://toppakou.com/info1/download/27_ADVANCE_母集団と標本・仮説検定/【学習指導案】27A_02_母集団と標本/仮説検定.docx
【文字おこし】
今回は、高校情報科目で習う統計学の母集団と標本、推定と検定の概要、Z検定、t検定について説明します。
はじめに母集団と標本について、身近な例と紐づけながら説明していきます。
とある和菓子工場ではどら焼きを1日10万個つくっています。
通常、どら焼きの重さの平均は100グラムとしています。
本当に平均100グラムかを知るためには10万個ぜんぶの重さをはかることですが、現実的ではありません。
そこで、全部の中から無作為に抽出した一定個数の重さを図って、全体を知る手法が用いられます。
具体的な例を統計学の用語と照らし合わせながら説明していきます。
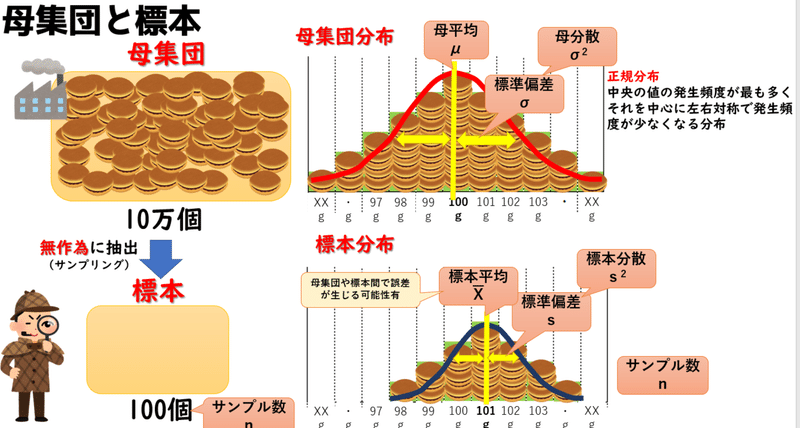
1日に製造するどら焼き10万個が全量として、その調査や観察の対象とする集団全体のことを母集団と言います。
どら焼きの重さのあるべき姿は平均100グラムです。
平均なので、99グラムの物もあれば、101グラムの物もあります。
以前説明したように、世の中の自然現象や社会現象の多くは正規分布となります。
中央の値の発生頻度が最も多く、それを中心に左右対称で発生頻度が少なくなる分布を正規分布と言います。
今回のどら焼きの重さも正規分布になるとします。
左右対称なので中央の一番高い山が平均値となり今回のあるべき姿の場合は100グラムとなります。
この母集団の中の平均値を母平均と言い μミューという記号で表します。
この集団の散らばり具合は、以前説明したように分散や標準偏差であらわします。
母集団の標準偏差はσ(シグマ)という記号で表します。そして母集団の分散は母分散と言い標準偏差の2乗つまりσ(シグマ)の2乗で表すことができます。
10万個のどらやきのおもさを全て図って平均が100グラムになるか、それとも機器の故障の影響でそうではないかを調べるためには10万個すべての重さを調べるのは現実的ではありません。
なのでこの母集団から一定数のどら焼きを抽出してその重さの平均をはかることにします。
その抽出する場合には、無作為に抽出することが重要です。
例えば、99という数字が好きだから99グラムのどら焼きだけ抽出するのはNGです。
中心当たりのどらやきが最も多いので、無作為に抽出すると、確率的に100グラム前後のどら焼きが抽出できる可能性が高くなってきます。
今回は10万個の母集団のなかから無作為に100個のどら焼きをとってきたとします。
この抽出された集団を標本と言い、1組の標本中のデータ数をサンプル数と言いい、nで表します。
標本も母集団と同様に正規分布になり、標本の平均を標本平均といい、エックスバーの記号で表します、標本の標準偏差はsの記号であらわし、分散はsの2乗となります。
サンプル数が母集団の数に近づくほど、母集団の平均や分散に近くなっていきますが、全量調査しているわけではないので、母集団と誤差が生じます。
また、おなじ100個でも1回目で抽出した標本データと、2回目に抽出した標本データの間でも誤差が生じる可能性があります。
――――――――――
多くの場合、母集団の平均値や分散が分かりません。
標本をもとにして調査し確率的に母集団がどのような値を持っているかを推測することを、推定と言います。
テキスト的な表現だと、「標本における一定の法則を母集団に当てはめて推し量る」ことを推定といいます。
推定には、母平均μ=100と言ったように1点で表す 点推定や
95≦μ≦105 と言ったように推定値に一定の幅を持たせる区間推定があります。
――――
標本のデータから、母集団にかんする仮説の真偽を判定する方法のことを仮説検定と言います。
簡単な例で説明していきます。本来数十万とか大きい数ですが簡単にするために、あえて少ない数で説明します。
人口10万人のミライ王国で200人を無作為に選んだところ、女性が130人、男性が70であった。
この標本データからだけ言える事実は「ミライ王国では女性の方が多い」ということです。
ただ、母集団を調べているわけではないので、これは仮説になります。
この仮説に対する反論として、「ミライ王国の男女比は半々のはず。たまたま、女性の方が多く取れただけ。女性が多いのは偶然のいたずらです」という意見がでたとします。
この女性が多いという立証したい仮説を対立仮説といいます。
それに対立する、男女比は半々という意見を帰無仮説と言います。
仮説検定では、「帰無仮説」の方が正しいという前提に立ちます。
つまり男女比が半々という仮説を正として、今回のように200人抽出して130人以上が女性になるという偏った結果になるのはどれくらいの確率で起こり得るのかを計算します。
この確率のことをp値といいます。p値0.05と言ったら百分率で表すと5%の確率という意味になります。
統計学の世界ではこのP値が5%未満だった場合は、めったに起こらないことが起きたとして、対立仮説が正しいと判断します。逆に言えば帰無仮説は正しくないということになります。このことを帰無仮説を棄却すると言います。
このめったに起こらないことを有意性があるともいいます。
この帰無仮説を棄却する5%未満の基準を有意水準といいます。医療問題など慎重な判断が必要な場合は有意水準1%が使われることもあります。
かりに有意水準が5%を上回った場合は、帰無仮説を棄却せず、女性の方が多いという仮説を採択しない流れになります。
頭が混乱していると思うので、ヒストグラムのイメージ図使って説明していきます。
縦軸を確率、横軸を女性の人数とします。
男女比半々という帰無仮説を正しい前提とするので、ヒストグラムの平均つまり最も盛り上がっている部分も全体の半分の100人とします。
全体の面積の5%未満がこの部分で、この境目にあたる女性の人数を限界値と言います。
そして有意水準の領域にある女性人数125人より多い領域を棄却域といいます。
つまり、限界値である125人より多ければ有意水準の5%未満の領域なので、男女比半々という帰無仮説は棄却されます。
今回は有意水準を右の片側5%を基準にしましたが、これを片側検定といいます。
いまは、女性が多いことを実証しましが、
仮に男女比がアンバランスという仮説を検証する場合は、女性が多い場合と男性が多い場合が考えられるので両側に設定する必要があります。
この場合は5%を左右で按分して、2.5%ずつ左右に棄却域を設けることになります。
これを両側検定といいます。
検定は何種類かありますが、母集団の正規分布に従っていて、
母平均と母分散が既に分かっている場合に使われる検定にZ検定があります。
標本平均と母平均が統計的に見て等しいといえるか検定する方法になります。
標本平均に対するZ値を求めて、それが標準正規分布のどこに位置するかで帰無仮説を棄却するか否かを決定します。
Z値は以前の動画で説明しましたが
あるデータxが平均値μからどれだけ離れているかを、標準偏差σを単位として示した値のことになります。
★例題
今のZ検定は、母分散が分かっていましたが、母分散が分からない場合はt検定というものを使います。サンプル数が30未満と少ない標本の場合に使われます。
母集団から抽出した標本平均の分布は正規分布に似た釣り鐘型になります。
この分布をt分布と言います。
これを聞いてZ値を思い出した方も多いと思います。
標準正規分布のZ値に相当する統計量がt値になります。ただしt値、―4~4の範囲より広くなります。
t値を求める上で、母分散の推定値である不偏分散を求める必要があります。
さきに自由度という言葉を説明します。
自由度は、自由に決められる数のことです。
たとえば平均値が既に決まっていた場合で4つの値を入力できる欄があったとします。
平均10とすると 1つめ8、二つ目11、3つめ10とした場合、平均10にするためには、4つめは11にしなければいけません。
この場合、4つのうち3つ自由に決められるので、自由度は3となります。
サンプル数がnとした場合、自由度はn―1で表されます。
今までの知識で、分散を求めるには
データ数分の平均との差の2二乗を足し合わせたものであらわしました。
不偏分散を求める式の分母は サンプル数マイナス1をします。
標本の特性上、元となった母集団の母分散に比べて分散が小さくなる傾向があります。
サンプル数マイナス1をして分母を小さくすれば、得られる値は大きくなります。
サンプル数n―1をして、標本の分散である分散を母分散に近づけるという役割をします。
★t値の公式パワポ
求めたt値が、全体の何パーセントに位置するかを調べるには自由度と有意水準で表される t分布表と突き合わせを行います。
正確には仮説を成り立たせる確率である信頼度というものも存在します。今回は信頼度95%の表になりますが、高校の情報の教科書にはそこまで言及していないので信頼度の詳しい説明は割愛します。
t分布表については、この後行う例題で具体的にどのように見るかを説明します。
それではt検定に関する、例題を解いて行きましょう。
★例題
t検定は、2標本間の有意差を調べる場合にも用いられます。
私用で高校の説明会に何校か行きましたが、話題にでてくるのが、YouTube教育動画についてです。
予習は予備校講師のYouTube動画を使ってもらい、授業はそれが分かっている前提で対面でしかできない内容で行いますや
「先生がYouTuberやってます」とか生徒会長が自慢げに語っている学校もありました。
これは、公立高校の情報教諭のブログ記事ですが、
コロナの影響で授業動画をYouTubeにアップしてそれで勉強してもらったら、テストの平均点が大幅に伸びたという話題です。
いつもの感覚なら平均70点前後のはずが、平均85点くらいだったらしく、わからないところを何度も見直せるなどの利点があったためなどが考えられます。
このような効果の検証にも、t検定は有効です。
立証したい仮説を YouTube動画は成績アップに効果がある。
反対意見の帰無仮説は、 YouTube動画は成績アップに効果はない。平均点に差が出たのはたまたま として
YouTube動画での学習を取り込んだクラスのテスト結果の標本と今まで通りの授業を行った標本からt値を求める方法が考えられます。
t検定は何種類かあります。
対応のあるt検定と対応のないt検定
対応のあるとは、同じ人、同じ物と考えてください。
例として同じクラスの生徒が受験した2つの試験結果の比較などがあげられます。
一方、対応のないとは違う人、違う物と考えてください。
対象が同じでも、同じ分散を持つ標本と異なる分散を持つ標本でわかれます。
同じ分散を持つ標本の例として、A組はYouTube動画で勉強を行った集団。B組はYouTube動画を使わずに勉強を行った集団として、同じテストを受験した2つのクラスを比較する検定が考えられます。
異なる分散を持つ標本の例としては
去年と今年の生徒が受験した異なる2つの試験結果を比較する検定が考えられます。
今日の授業は今まで大学で扱っていた統計学の一部が高校情報Ⅰの教科書にとりこまれていて、かなり難易度が高く感じたと思います。
統計学に関しては、さらに掘り下げた分かりやすいYouTube動画が沢山あるので興味があればさらに知識を深めていきましょう。
今日の授業は以上になります。最後までご視聴ありがとうございました。
【解説重要用語】
母集団、標本、母平均μ、母分散 σ2乗、標準偏差σ、正規分布、標本平均 Xバー、標本分差 sの2乗、サンプル数n、サンプリング、点推定、区間推定、仮説検定、帰無仮説、帰無仮説を棄却する、対立仮説、p値、有意水準、有意性、片側検定、両側検定、Z検定、自由度、t分布表、不偏分散
★私の目標
「とある男が授業をしてみた」 の葉一さん
https://www.youtube.com/user/toaruotokohaichi
※Google社に招待頂いた、「YouTube教育クリエイターサミット2020」で
葉一さんと文部科学省・Google役員の対談セッションに感銘を受けて、高校情報講座スタートしています。
【参考サイト・参考文献】
P値と帰無仮説について専門用語も数式も使わずにざっくりとしたイメージを説明してしまう動画 – YouTube
https://www.youtube.com/watch?v=y0g7OuJpTno
熊野コミチ 統計とお仕事チャンネル – YouTube
https://www.youtube.com/channel/UCxGR5omDLIXBu6yOrvOJ-2w
予備校のノリで学ぶ「大学の数学・物理」 - YouTube
https://www.youtube.com/channel/UCqmWJJolqAgjIdLqK3zD1QQ
都立高校 情報科教諭ブログ
https://inagaki-shunsuke.jp/
数学嫌いのための社会統計学〔第2版〕
https://www.amazon.co.jp/s?k=%E7%B5%B1%E8%A8%88%E5%AD%A6+%E6%95%B0%E5%AD%A6%E5%AB%8C%E3%81%84&ref=nb_sb_noss
※佛教大学 情報科教員養成 基礎統計学のテキスト
文部科学省 「情報Ⅰ」教員研修用教材
https://www.mext.go.jp/a_menu/shotou/zyouhou/detail/1416756.htm
詳細(情I703 高校情報I Python)|情報|高等学校 教科書・副教材|実教出版 (jikkyo.co.jp) 検定通過版
https://www.jikkyo.co.jp/book/detail/22023322
令和4年度新版教科書「情報Ⅰ」|高等学校 情報|日本文教出版 (nichibun-g.co.jp)検定通過版
https://www.nichibun-g.co.jp/textbooks/joho/2022_joho01_1/textbook/













※コメント投稿者のブログIDはブログ作成者のみに通知されます