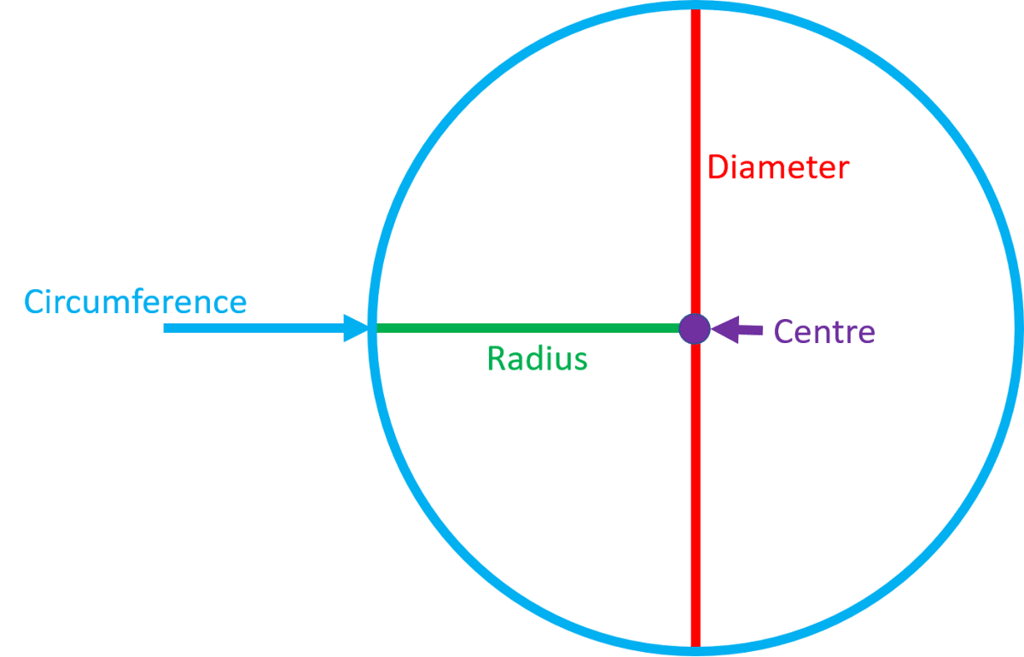
私たちは皆、私たちが円と呼ぶものが丸い形のオブジェクトであることを知っています。それで、円の長さを測定することになると、その丸い形で何をするべきでしょうか?円形体の長さを測定することは可能ですか?
はい、円の長さを測定することは可能ですが、他の真っ直ぐな物体の測定とはかなり異なります。この点で、中点計算機などのオンライン計算機も役立ちます。
円の長さを測定するには、円の円周を調べる必要があります。一方、円の円周を調べるには、円の半径または直径を調べる必要があります。直径または半径とともに別の測定が必要であり、それはπの値です(piとして発音)。幸いなことに、piの値が与えられているため、急いでその値を見つける必要はありません。
円周(円の周りの直線距離または単に円の長さ)を見つけるために必要なことは、円の半径または直径の値を見つけることだけです。
直径または半径の値がないと、円の円周(長さ)を見つけることができません。そのため、ここでこれらの円の長さの測定方法についてご案内します。
円の半径とは何ですか?
円の中心から円の周りの直線距離の任意の点までの距離は、円の半径として知られています。簡単に言えば、円の中心(中点)から円の終わりに向かって直線を引くと、円の半径と呼ばれます。
円の半径を明確に描写するには、次の図をご覧ください。
さあ、あなたの番です!以下に示す図を見て、これらのどれが円の半径に従ってセグメント化されているかを見つけてください。
では、次のコンセプトであるに進みましょう。
円の直径は?
円の直径は、円の中心を通る直線としてマークできます。両側からの直線の端点は、円の円周に接続します。簡単に言えば、直径は円の半径の2倍の長さです。以下の図をご覧ください。
これで、円の半径と直径がわかったので、先に進んで円の円周について説明します。
円の円周とは何ですか?
簡単に言えば、円周は円の周りの直線距離です。これは、円が外側に直線に分割されているため、円の長さであることを意味します。したがって、ここでは円の半径と直径を使用します。半径と直径の両方は、円の線形セグメントの測定値です。したがって、円の円周の値を見つけるには、これらの測定値のいずれかが必要です。
円の円周の公式を見てみましょう。
円周式とは何ですか?
円周の式は次のとおりです。
C =πd
一方、Cは円周を表し、dは直径を表します。
πの値が3.14であり、円の直径が半径の2倍であることはすでにわかっているため、知る必要があるのは円の半径の値だけです。
したがって、円の直径の値を使用して、円の円周を計算できます。行う必要があるのは、piの値に直径の値を掛けることだけです。 πとdの積は、円のCの値になります。
まあ、これは円の円周を測定する手動の方法です。オンライン円周計算機を使用して、円の半径の値を入力するだけで円の円周を測定できます。