すべてのレベルの分析化学では、グラム、モル、および変換を理解する必要があります。どの学年でも教えられる基本的なことは、ほくろです。ほくろとその理解なしでは、化学とその応用の高度な概念を理解することはできません。これらの概念について詳しく見てみましょう。
グラムとは何ですか?
これは、質量単位のメートル法です。これは、氷の融解温度でメートルの100分の1立方メートル[1cm³]に等しい純水の体積の絶対重量として定義されます。
SI基本単位:10-3キログラム
帝国単位米国慣習:0.0353オンス
ユニットシステム:UCUMベースユニットおよびCGSユニット
CGSユニット:1グラム
単位:質量
1 g in:等しい
用途:
一般的には、家庭用非液体成分の計算や世界中の食料品の買い物に使用されます。
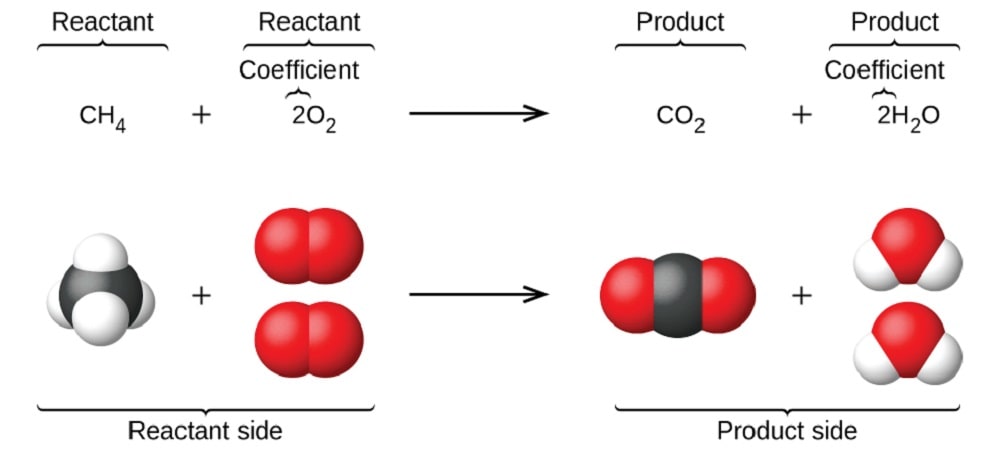
モル基本化学測定ユニット:
それは常に大学で私のお気に入りのトピックであり、さまざまな化合物のモルを計算するのも大好きだと確信しています。これは、測定用の別のユニットにすぎません。モル比を即座に確認するために「モル分数計算機」を使用できます。さらに、以前のユニットが適切でなくなったときに新しいユニットが開発されます。グラムを含む化学計算では、さまざまな化合物や化学物質を測定しながら混乱が生じていました。
あなたが大学生で、計算が難しいと思う場合、オンラインの「モルからグラムへの計算機」がこの問題を大いに助けてくれます。
ほくろも再現可能なもので作られています。モルとは、12グラムの炭素12に含まれる粒子の数が等しいものの量です。その粒子の数は、アボガドロの数、約6.02x1023です。炭素原子のモルは6.02x1023炭素原子です。したがって、6.02x1023の炭素原子の代わりに1つのモルを書くのは非常に簡単です。長い計算をしながら、物事を簡単に変換して理解できます。
モルからグラムの計算
これは最も一般的に使用される化学計算の1つであり、すべての人が正確に計算する必要があります。そうしないと、結果が非常に不正確になります。反応物と試薬のモル比は、「理論収量」を確認した後にのみ使用されます。通常、周期表から取得されるこの変換には原子質量が必要です。基本的な原子質量は、ほとんどすべての化学の学生によって暗記されています。それらがなければ、それらは化学のあらゆる分野でゼロのようです。変換とその式を簡単に理解するのに役立つ簡単な例の1つを見てみましょう。
例:
0.2モルのCO2には何グラムの二酸化炭素が含まれていますか?
今、炭素と酸素の原子質量を見てください。これは、原子のモルあたりのグラム数です。
炭素(C)は1モルあたり12.01グラムです。
酸素(O)は1モルあたり16.00グラムです。
二酸化炭素の1分子には、1つの炭素原子と2つの酸素原子が含まれています。
CO2モルあたりのグラム数= 12.01 + [2 x 16.00]
モルCO2あたりのグラム数= 12.01 + 32.00
CO2モルあたりのグラム数= 44.01グラム/モル
モルあたりのこのグラム数に、最終的な答えを得るために必要なモル数を掛けるだけです。
0.2モルのCO2のグラム= 0.2モルx 44.01グラム/モル
0.2モルのCO2のグラム= 8.80グラム
特定のユニットをキャンセルして、必要なユニットを提供することをお勧めします。この場合、モルは計算からキャンセルされ、グラムが残ります。
グラムをモルに変換することもできます。どちらも相互交換可能であり、それほど難しくありません。これを試して、それがあなたにとって非常に簡単であることを願っています。











 いものであり、このタイプのデータを解釈することは非常に難しい作業です。
いものであり、このタイプのデータを解釈することは非常に難しい作業です。