みなさんは、「開閉サージ」という現象をご存知ですか?電子機器の電源スイッチを入り切りしたときなどに、時々ピカッとスパークが飛ぶことがありますね。あれが開閉サージの仕業です。いったい何であんなことが起こるのでしょう。原因は回路の中のインダクタンス(コイル)にあります。実は、同様のことがコンデンサでも起こります。コンデンサとコイルは相補性のような関係にありますが、電荷を溜めたコンデンサの端子をショートすると、理屈上∞放電電流が流れますね。これは電流サージと言えます。よって、インダクタンスによるサージ電圧を「電圧放電」という人もいます。
さて、電流が流れているインダクタンスは(LI^2)/2のエネルギを蓄えています(コンデンサの場合は(CV^2)/2ですね)。このエネルギが開閉サージの源です。では、サージを検討する準備運動としてLR回路の動作を考えてみましょう。
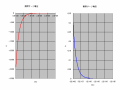
左図の回路で、スイッチが電源から0Vに切り換った場合のi(t)とv(t)の動作を考えます。これは前にやったLR回路の、スイッチの切り換りが逆になっただけですね。
回路の微分方程式は
Ldi(t)/dt+Ri(t)=v(t) ----- ①
(初期条件 i(0)=E/R v(t)=0 )
式①をラプラス変換し
L{sI-i(0)}+RI=V
(初期条件i(0)=E/R v(t)=0 より)
LsI+RI=V+i(0)L LsI+RI=LE/R (Ls+R)I=LE/R
分母分子をLでわって
I=(LE/R)/ (Ls+R) I=(E/R)/ (s+R/L)
[ f(t)=e^at ⇔ F(s)=1/ (s-a) の変換式より ]
逆ラプラス変換すると
i(t)=E/R e^-(R/L) t が得られます。
これがこの回路の方程式です。簡単ですね。さて、では右図の場合はどうでしょう。0VラインにRsが入りました。スイッチが0V側に切り換れば電流i(t)がRsを流れますね。ということは、v(t)=-Rsi(t)になりますね。仮にスイッチが電源につながっているときの回路電流を1Aとし、またRsを100kΩとして、スイッチが0V側に切り換ったらv(t)は何Vになるでしょう。瞬間値としてv(t)=-100kVになります。ものすごい高電圧ですね。これがインダクタンスによる開閉サージです。
これが発生すると同じ電線につながっている他の機器を壊したりするので、サージは一般に悪者扱いされ忌み嫌われます。バリスタなんて素子が考え出されたのも、このサージ電圧をなんとか低減させようとして生まれた産物です。
さてRs=0の場合は左図と同じで回路電流は
i(t)=E/R e^-(R/L) t ですね。
この式のE/R と e^-(R/L) tを分けて考えると
E/Rは回路の最大電流
e^-(R/L) t は時間経過に伴う減衰を意味しています
e^-(R/L) 0 =1、以降tの増加とともに0に近づいていきます。
スイッチが電源側のときはE/Rが電流の最大値であり、Rsはまったく関与しません。スイッチが0V側に切り換ると、RとRsが直列となって減衰に関与することが図から明らかですね。よってこの場合のi(t)の方程式は
i(t)=E/R e^-{ (RL+R) /L} t となります。
サージ電圧v(t)は、このi(t)と-Rsをかけたもの
v(t)=-RsE/R e^-{ (RL+R) /L} t となります。
関連記事:
開閉サージ の考察② 2009-06-17
LCR回路の過渡特性 2009-05-11