フーリエ変換とラプラス変換。
電気回路でのCRフィルタや、「バネ-質量系」の振幅倍率など、周波数特性を知りたい場合にはこの両者は真骨頂とも言える威力を発揮します。LCR回路をラプラス変換した折に、インピーダンス(Ls+R+1/Cs)が現れ、これの逆数1/(Ls+R+1/Cs)を伝達関数といいましたね。実はこの「伝達関数」が周波数特性なのです。
CRのローパスフィルタでやってみましょう。
L[交流電源] =Eo
L[出力電圧] =Ec
インピーダンス =R+1/Cs
とすると
Ec=Eo{(1/Cs) / ( R+1/Cs)} という式になって
Ec/ Eo=(1/Cs) / ( R+1/Cs)
Ec/ Eo=(1/sCR) / ( 1+1/sCR) 分母分子にsCRをかけて
Ec/ Eo=1/ ( sCR+1) ----- ① となります。
これがCRローパスフィルタの伝達関数の式です。右辺がCRローパスフィルタの中身を示しているということですね。
s=δ+jω として、ラプラス変換の式を記述すると
F(s)=∫[0-∞] f(t)・e^-δt ・e^-jωt dt ですが
ここでδ=0とすれば(周波数特性では不要)ラプラス変換の式は
F(s)=∫[0-∞] f(t)・e^-jωt dt となります。
これはフーリエ変換そのものですね。
(t < 0)の範囲で f(t)=0 となる関数の場合、
フーリエ積分の範囲を( 0≦ t ≦∞)としても結果は変わりません。
よって、CRローパスフィルタの伝達関数
Ec/ Eo=1/ ( sCR+1) のsは s=jω としてよいということです。
sをjωに書き換えます。
Ec/ Eo=1/ ( jωCR+1) ----- ②
ここでCRに値を入れましょう。カットオフ周波数をfc=100Hzに決めれば
ωc/2π=100 ωc=100・2π 1/(CR)=628.32 CR=1.6m
Ec/ Eo=1/ ( jω1.6m +1 ) ----- ②-2
複素数の絶対値を求めます。
[Ec/ Eo]=1/√{1+(ω1.6m)^2}
これが振幅特性です。
位相を求めます。
絶対値[Ec/ Eo]=1/√{1+(ω1.6m)^2} より
∠(Ec/ Eo)=-tan(-1)ω1.6m
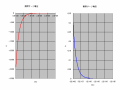
以上の計算によって求めた振幅比と位相の周波数特性は図のようになります。つまり、周波数特性を求める場合は、伝達関数のsをjωに置き換えればよいということですね。
関連記事:
周波数変換(フーリエ変換)2009-07-12
フーリエ変換とラプラス変換 2009-06-20
電気回路でのCRフィルタや、「バネ-質量系」の振幅倍率など、周波数特性を知りたい場合にはこの両者は真骨頂とも言える威力を発揮します。LCR回路をラプラス変換した折に、インピーダンス(Ls+R+1/Cs)が現れ、これの逆数1/(Ls+R+1/Cs)を伝達関数といいましたね。実はこの「伝達関数」が周波数特性なのです。
CRのローパスフィルタでやってみましょう。
L[交流電源] =Eo
L[出力電圧] =Ec
インピーダンス =R+1/Cs
とすると
Ec=Eo{(1/Cs) / ( R+1/Cs)} という式になって
Ec/ Eo=(1/Cs) / ( R+1/Cs)
Ec/ Eo=(1/sCR) / ( 1+1/sCR) 分母分子にsCRをかけて
Ec/ Eo=1/ ( sCR+1) ----- ① となります。
これがCRローパスフィルタの伝達関数の式です。右辺がCRローパスフィルタの中身を示しているということですね。
s=δ+jω として、ラプラス変換の式を記述すると
F(s)=∫[0-∞] f(t)・e^-δt ・e^-jωt dt ですが
ここでδ=0とすれば(周波数特性では不要)ラプラス変換の式は
F(s)=∫[0-∞] f(t)・e^-jωt dt となります。
これはフーリエ変換そのものですね。
(t < 0)の範囲で f(t)=0 となる関数の場合、
フーリエ積分の範囲を( 0≦ t ≦∞)としても結果は変わりません。
よって、CRローパスフィルタの伝達関数
Ec/ Eo=1/ ( sCR+1) のsは s=jω としてよいということです。
sをjωに書き換えます。
Ec/ Eo=1/ ( jωCR+1) ----- ②
ここでCRに値を入れましょう。カットオフ周波数をfc=100Hzに決めれば
ωc/2π=100 ωc=100・2π 1/(CR)=628.32 CR=1.6m
Ec/ Eo=1/ ( jω1.6m +1 ) ----- ②-2
複素数の絶対値を求めます。
[Ec/ Eo]=1/√{1+(ω1.6m)^2}
これが振幅特性です。
位相を求めます。
絶対値[Ec/ Eo]=1/√{1+(ω1.6m)^2} より
∠(Ec/ Eo)=-tan(-1)ω1.6m
以上の計算によって求めた振幅比と位相の周波数特性は図のようになります。つまり、周波数特性を求める場合は、伝達関数のsをjωに置き換えればよいということですね。
関連記事:
周波数変換(フーリエ変換)2009-07-12
フーリエ変換とラプラス変換 2009-06-20