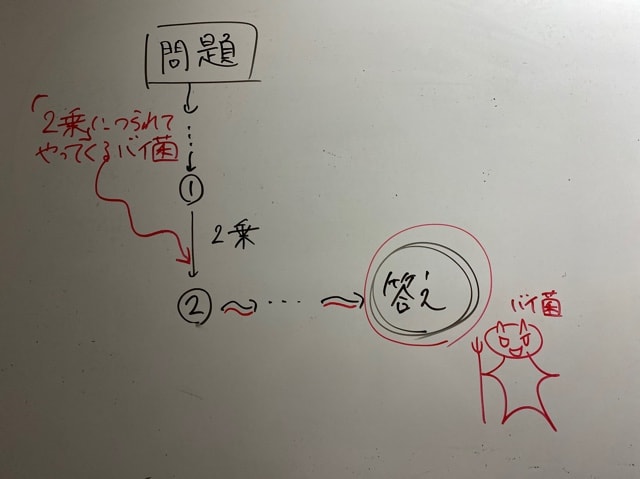
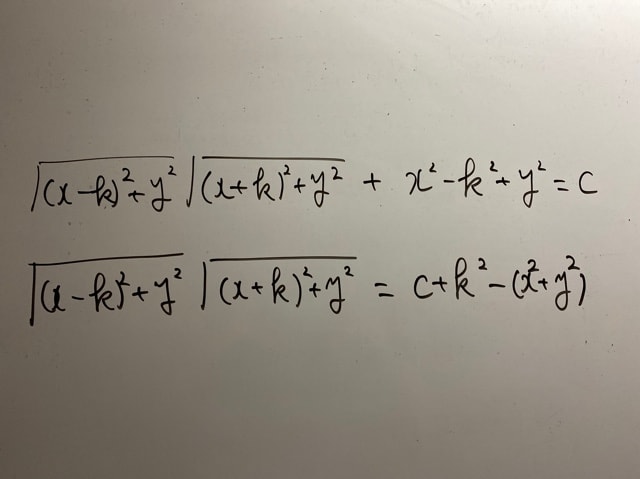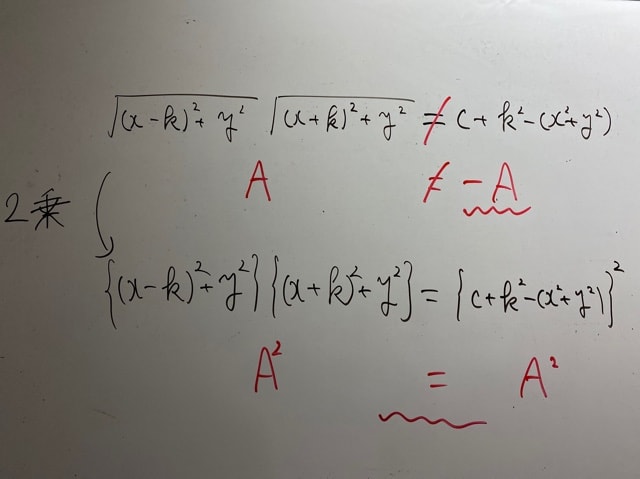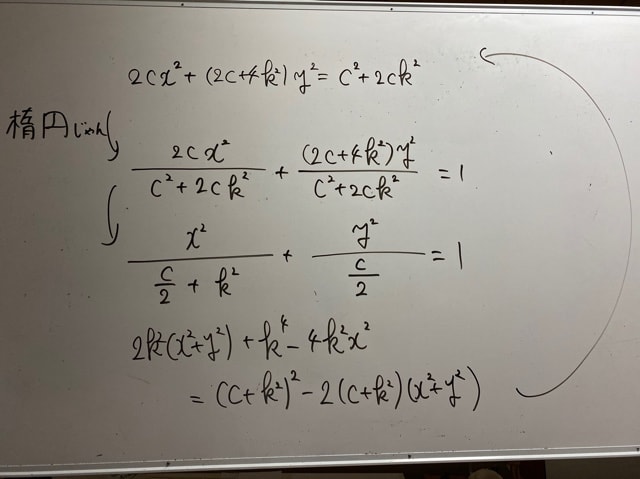死に戻り…………



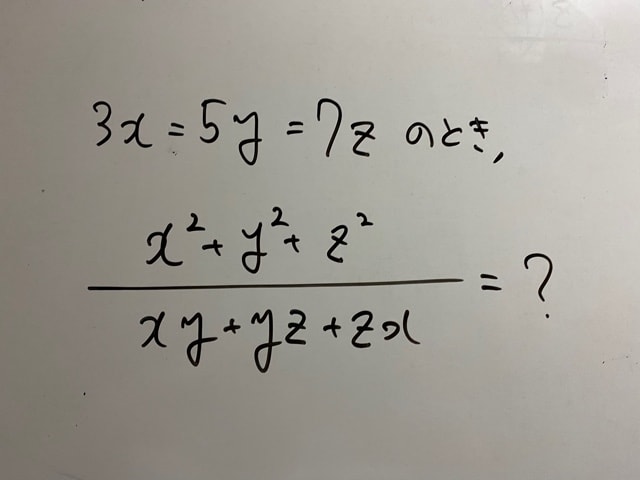


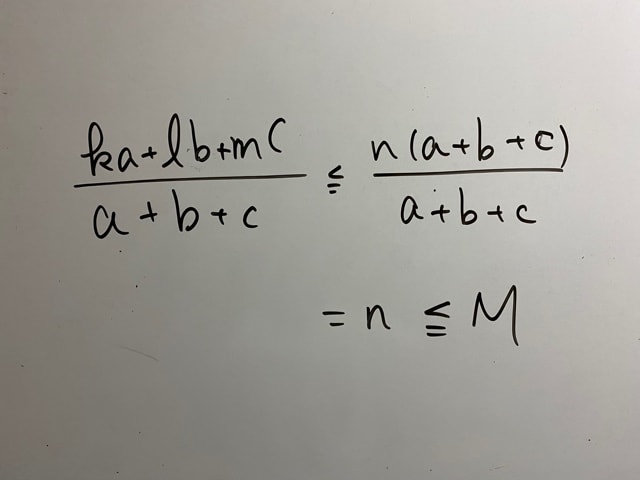
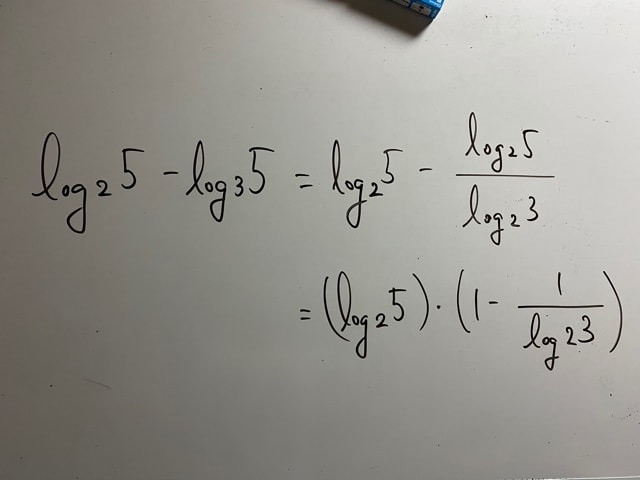
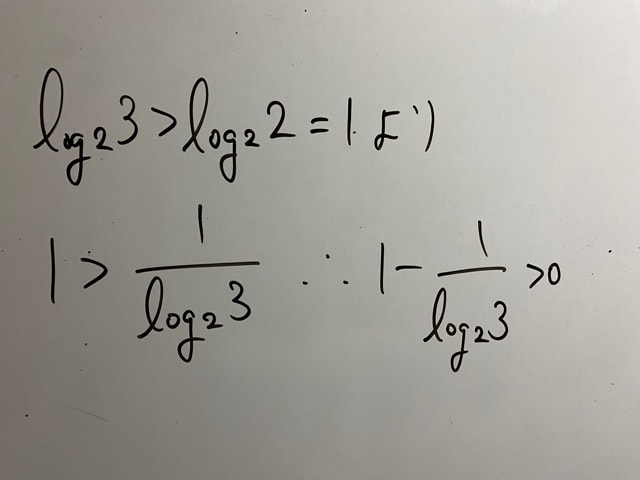

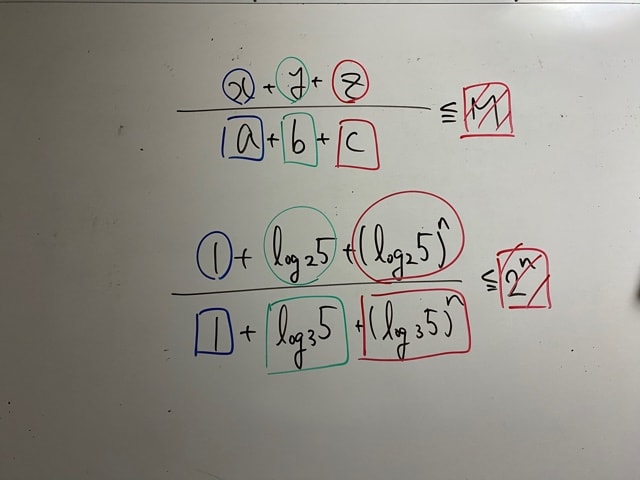
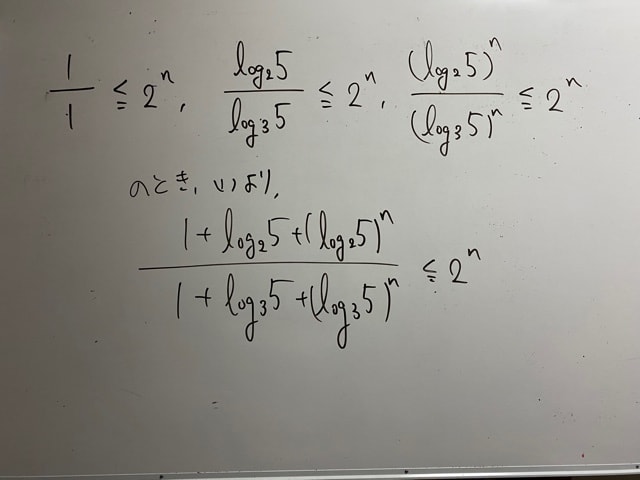
(答案にいきなりこれ書いたらダメですよ!これはメモ!なぜなら…)



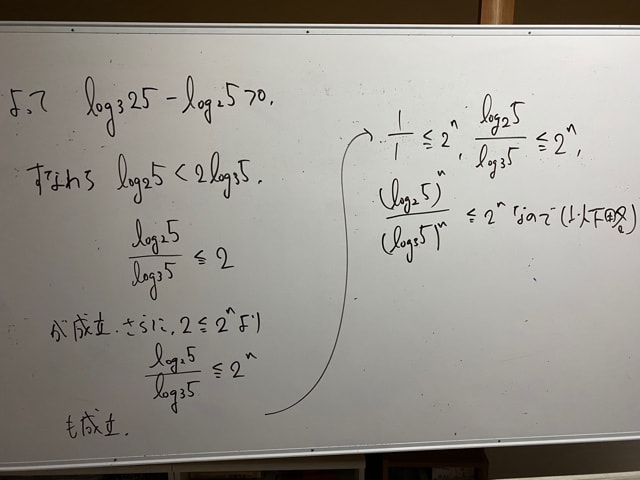
実はこれを書く前に3000字ほど書いてたんですが、何があったかわからないのですが一瞬にして全て消えてしまいました。
コロナウイルスでオンライン実習なこと、病院にコロナウイルスを持ち込んではいけないこと、色々書いてたのですが全て消え去り、かなり悲しくなりました。これからは下書き保存します。
今度気が向いたときにもう一回書くことにして数学します。
本日は2019年筑波大学理系数学の2番。

(1)の式と(3)の式はなんか似てますね、形が。
(2)の数字は(3)に使われてますね。
(1)〜(3)は繋がっていそうです。
では、(1)をさっそく攻略しましょう。
不等式の証明ですが、基本は
[大とされているもの]-[小とされているもの]
の式を作り、これが0以上(もしくは0より大きい)を示すんですよね。例に漏れず、これもそうしちゃいましょう。

さて、この分数を計算します。

そしたら、こんなふうに0以上と示されます!x/a,y/b,z/cは全てM以下、a,b,cは正の実数なので!!(記述はちゃんと書いてくださいね)
あっけないので、別の解き方も少し探してみましょう。
この問題、x+y+z/a+b+cですが、こんな繋がった分数を見ると、あの問題を思い出します。
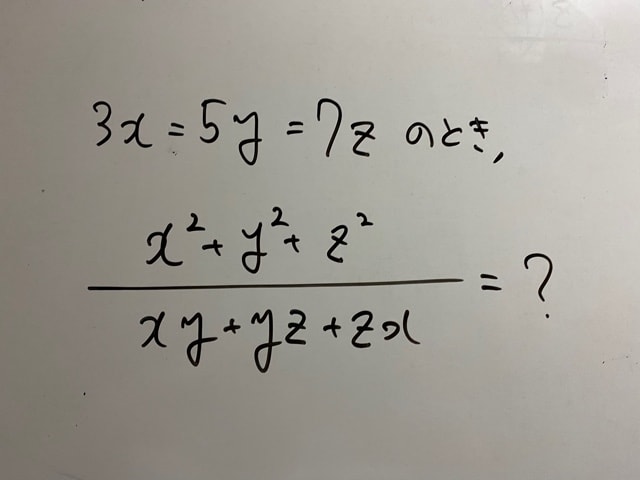
分母が0にならないよう問題はx,y,zに配慮しないといけないんですが、今は置いておいて。
解法を知っている方は、
「=kとおく」
という方針が打ち立てられると思います。
そしてx=k/3、y=k/5、z=k/7として、代入です。
僕はこれに似た方針をこの筑波の問題に取り込みました。

同じように、x=ka、y=lb、z=mcとして、代入してみましょう。

k,l,mのなかで1番大きなものに注目してください。k,l,mのどれが1番大きいかはわかりませんが、それをnとすると、
ka+lb+mc≦na+nb+nc=n(a+b+c)
という計算ができます。
nはk,l,mのいずれかなので、n≦Mが成立していることを考えると、
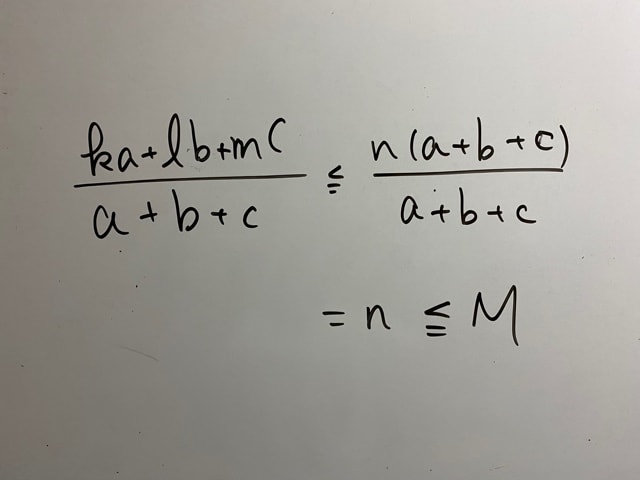
このとおり、≦Mが示せます。
不等式証明の基本である大-小からは外れてしまいますが、一応これを別解としておきましょう。
次に(2)です。見ただけで「いや、そりゃ底の小さいほうでしょう!」と言いたくなりますが、問題となっているからには説明しないといけませんね。だからといって「底の小さいほうが大きいです」とか言うのはなんか違います。
まあこれも不等式ですし、一応引き算くらいして証明しましょう。大きいとされるほうは問題には明記されてませんが、底が小さいほうだっていうのは問題を解いている皆さんがもうご存知ですよね?
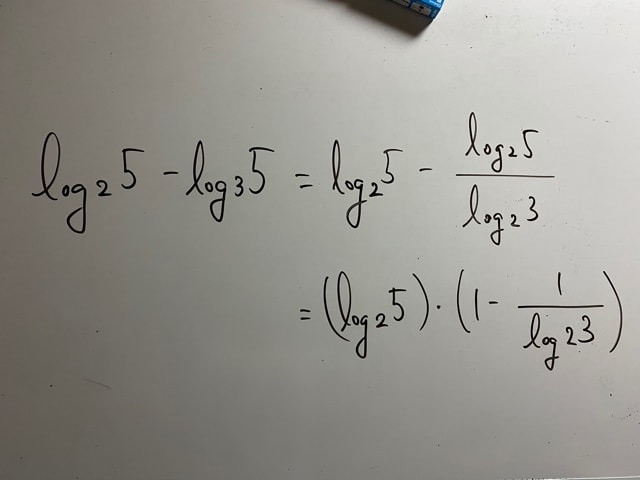
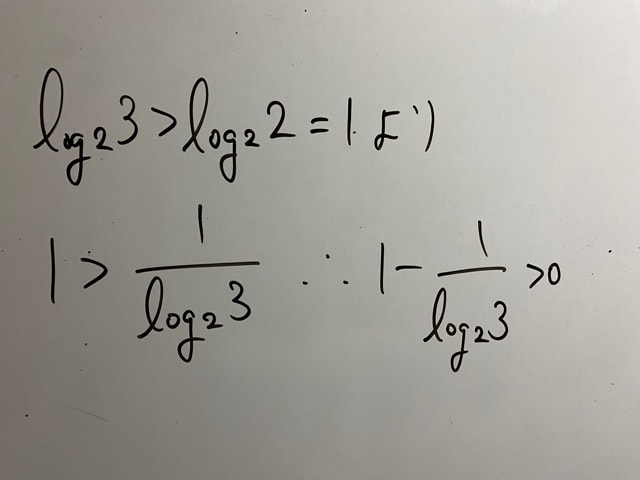
よって、元の式は>0なので……的なので良いでしょう。
これもとんでもなくあっけないですね。別解探しましょう。
一瞬「は?そんな当たり前のことを…何を今更…」って思った人は、背理法を考えたのではないでしょうか?証明しにくい問題は背理法やら待遇やらで解けという話がありますが、これも背理法で解けます。

こんなふうに解くの僕は好きです。本番なら引き算しますけど。
眠いので(3)に入ります(深夜3時半)。
ラスボス的風貌ですよね。この問題だけで出されたら、受験生はもしかしたら見た目の厳つさに捨ててしまうかもしれません。しかし、我々には(1)、(2)という強い味方がいるのです。さっそく攻略にかかりましょう。
(1)の形と(3)の形を比べてください。どこの文字がどの数字に対応しているのかを把握しましょう。
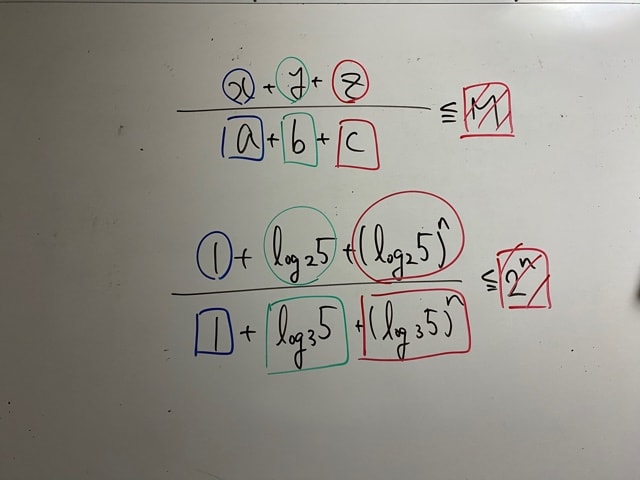
対応を見つけてしまったら簡単です。
(3)の数字で、(1)に倣えばいいのです。
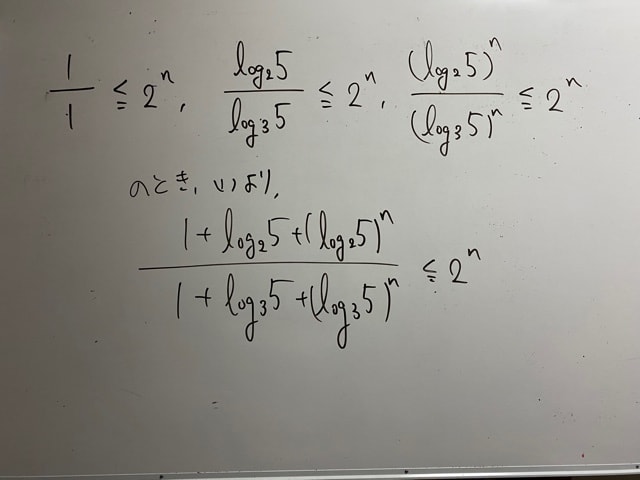
(答案にいきなりこれ書いたらダメですよ!これはメモ!なぜなら…)
あとは、上の3つの不等式のうち、右2つを証明すれば下の不等式が成り立つと言えます。
(まだ示していない式があるからです!示してからこの答案を書いて行きましょう!!)
1番右上の不等式ですが、全部がn乗ですよね。なので、n乗根をとったものを大小比較してあげればそれでよいです(眠いので説明が雑)。
ちょっと誰でも簡単に発想できる解法が思いつかなかったので少し難易度上げますが…

青文字の通りですよね。
(ちょっとlog○○の書き方が分からないので全部ホワイトボードに書いて誤魔化してるんです。写真ばっかりですが許してください)
で、大小を比較するその2数ですが、大体どれくらいの値なんでしょう?
両方ともに2を超えていることはわかります。でもどちらも3より小さい。
しかし、左の真数が25のやつのほうが、右の真数5のやつよりも3に近いと思いませんか??右の真数が5のやつのほうが2に近いと思いませんか??
だって、25は9に比べたらはるかに27に近いんです。底が3の対数は3に近いでしょう。5は8に比べたら4に近いんです。底が2の対数は2に近いでしょう。(あ く ま で 感覚です!!)

このような予想です。じゃあ、これを証明するならどうしましょう?
間の5/2をとってきて、それぞれと5/2の大小を考えてみるのが良さそうじゃないですか??

完璧ですね。
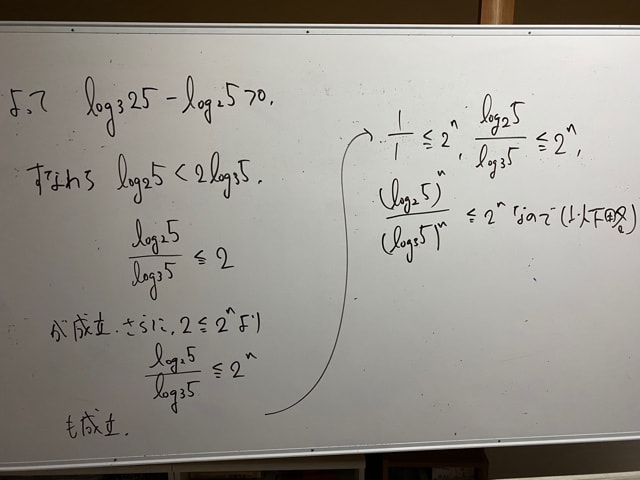
続きは4つ前?にあげた画像の通り。
さて、これで問題おーわり!!ではなくて、なんか問題にはもう片方に変なのついてましたよね。
1より大きいことを示さなければいけないんだとか。全然大したことありません。(2)で示したことをつかえば、分子の方が大きいことは簡単に証明できると思います(眠いので略)。
この問題では、大小をどうやって示すかをたくさん問われました。基本に従って引き算をするのもありですが、(2)のように当たり前すぎて引き算さえ思いつきにくいもの、(3)の途中に出てきたあの2数のように間に何か挟んでやるとやりやすいものなど、色々です。
(2)は引き算をしなくても、はたまた背理法をしなくても、底と真数をひっくり返して(つまり逆数にして)評価する方法とかもありますし、(3)は間に数字入れなくても(2)同様に底と真数をひっくり返したもの(つまり逆数にしたもの)を引き算して評価するなど、本当に色々です。
いっぱい勉強しましょう。いろんな見え方すると、楽しいですよ。
4時半です。おやすみなさい。
アクセント…………調べる根気が………