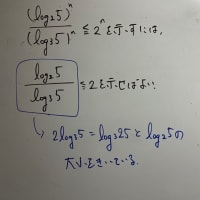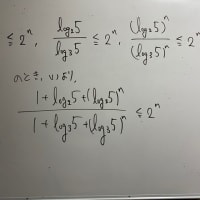書きたいときに書きたいことを書くスタンスを取ると、どうしても頻度は少しずつ減っていきますよね…だいたい指数関数的減少だと思っています。いや、それじゃあすぐ0になってしまうじゃないですか、不吉な。

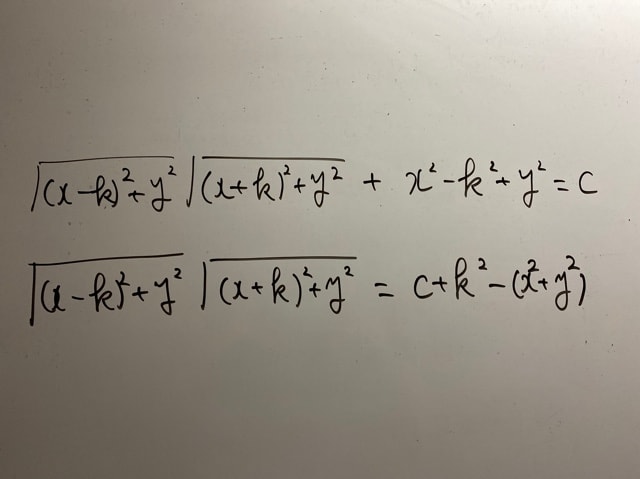

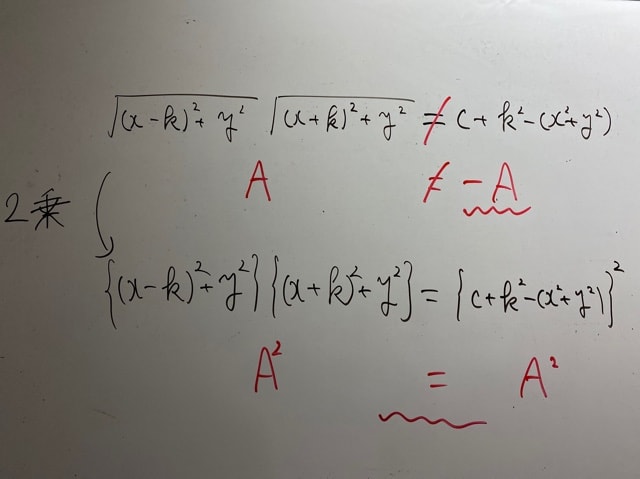





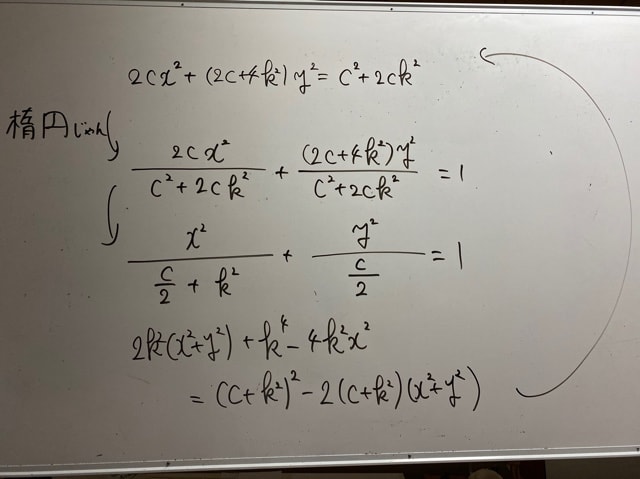

今日は数学しちゃおっかなぁ〜と思って、1つ問題を抜き出してきました。
1999年京都大学入学試験より
平面上に2定点A,Bをとる。cは正の定数として、平面上の点Pが
|PA||PB|+→(PA)・→(PB)=c
を満たすとき、点Pの軌跡を求めよ。
表記がわからなかったので……→(○)は「ベクトル○」を表していると思ってください。
あんまり各地で取り上げられることはない問題かと思います。かくいう僕も、「うわぁ!めっちゃいい問題ジャーン!」とはならないなぁ…。
"軌跡を求めよ!"の文言を見ただけでゲロを吐く方は本当に多いと思います。それもこれも媒介変数を絡めた問題たちのせいなのですが、この問題はそういった謎の数字は今のところ見あたらなさそうですね。解いているうちに出てくるかもしれませんが、そんな問題には僕は出会ったことないかも…(忘れてるだけかも)
この問題、Pの軌跡を求めるというわけですから、P(x,y)と置いてこのxとyの関係を見つけてあげたらいいと考えます。そこで問題になるのが、「え、でもAもBも座標で表されてないじゃないですか!」というもの。
座標が書いてないなら置いちゃえばいいじゃない!!
AとBは定点という条件しか与えられていませんので、全然具体的じゃないなぁと思うかもしれません。しかし、
A(k,0)、B(-k,0) (kは正の実数)
と置くだけで一般性を失わずに座標にのせることができます。具体的な縛りはなくものすごく自由な点たち(だからといってPのようにチョロチョロ動き回らない)です、「距離が100離れている」だったり「あるところから斜め45°むいて500離れてる」だったりするんです。それが直線ABを軸に、ABの中点を原点に置く座標系を考えてしまえば、全てのケースをA(k,0)、B(-k,0)などというたった1行で表現できてしまうだなんて神秘!とは思われませんか。
すごく話が逸れましたが、あとはバリボリ計算をしていければと思います。

整理しましょう。
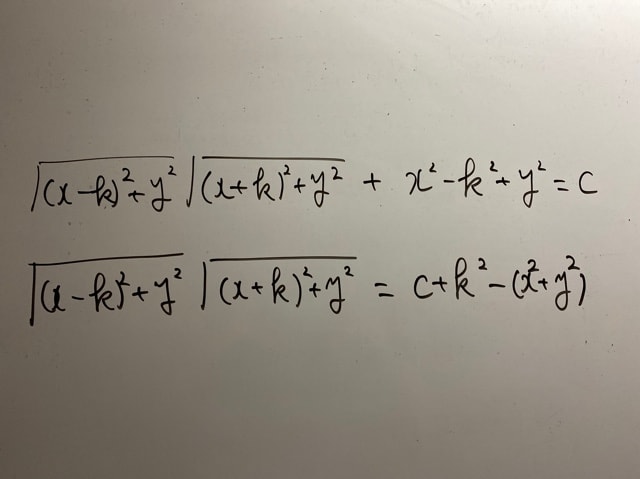
最後の式、明らかにルートだけ片方に残しています。目的は分かりますよね?もう2乗することしか頭にありません。
しかしここの2乗の操作の前に、xとyに条件が付きます。(ちょっとここから長い)
最後の式ですが、左辺が0以上の実数で計算されるはずですから、右辺も0以上の実数にならないといけないはずです。よって、c+k²≧x²+y²という条件が必要になります。
これがないとどうなるか…説明することが難しいんですけれど、トライしてみたいと思います。
仮に、さっきの写真の最後の式の左辺・右辺がともにAという数字(わかりにくければ8でも10でもなんでもどうぞ)になるようなx,yがあるとします。左辺は必ず0以上の実数ですから、A≧0です。
すると、2乗してももちろん両辺で=が成立することは問題ないでしょう。

次に、左辺がA、右辺が-Aとなるようなx,yがあると考えてください。A≠0のとき、もちろんこれはイコールが成立しません。(A=0は実は
k=0の場合のみで起こりうるもので、k=0は2定点A,Bが同一点になってしまいますから、今回は省くことにします。)
しかし、両辺を2乗すると、両辺ともA²となり、=が成立してしまいます。
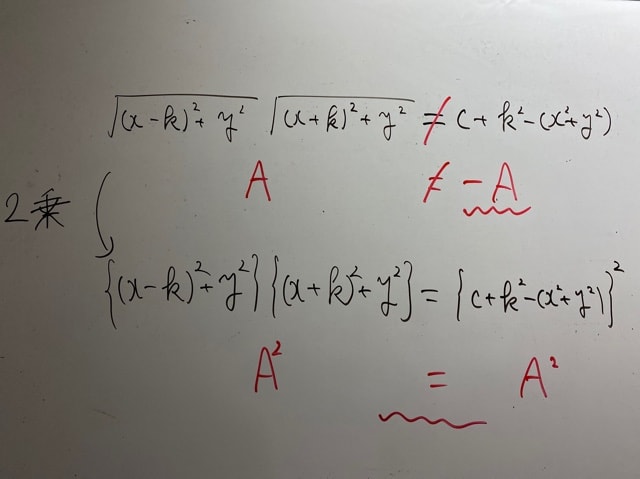
一体何が問題なんですか?それは、答えがどの式から導出されるかに関わります。

この2つの式ですが、①は問題の条件から立てられた式、②はそれを2乗し、今から整理して答えの形を暴くぞ!の式です。我々は②から答えを見出そうとしているのです。
しかし、②の式だけであれば、さっき見たように「①は成立しないけど②は成立するようなx,y」も許してしまうことになります。
これはまずいことです。②を弄って「やったぁ!答えだ!」と出た式は、①を成立させない(x,y)を答えに含めてしまっているのです。つまり、問題の条件に合わない(x,y)を答えていることになる…もう0点でしょう。
なので、②だけでなく、①が成立するための(x,y)の条件が必要なのです。その条件により、問題文に沿う答えが出てくるのです。
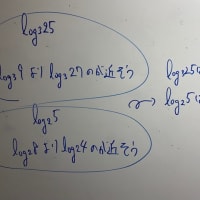
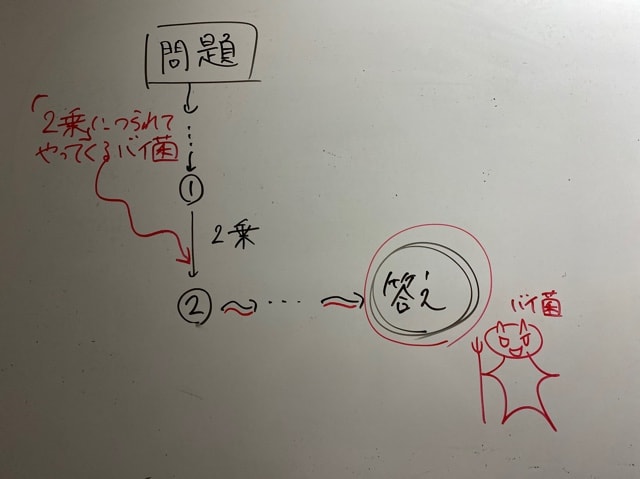
言葉の説明だけだとなんかアレなので、僕のイメージ図描きます。

どんな問題でも、香ばしい式変形のところでバイ菌が入ってくるんですよ。そのまま進めば、我々は感染した答えを出すことになります。そしてこの答えは、問題文の意図する条件だけでなく、バイ菌たる「問題の意図とは違う条件」のものまで映し出してしまうのです。
この問題においてバイ菌は「①では成り立たないけど②では成り立つ(x,y)」です。そして、バイ菌の侵入を許さない消毒液が、今回の問題にあたってはc+k²≧x²+y²という条件なのです。
じゃあ今度は、その消毒液によってバイ菌を断てたことをどう判断しましょうか?
それは、②から①へ戻るときにバイ菌コースが消えていることを確認すれば良いのです。

上は消毒液によるバイ菌コースぶっ壊しのイメージ図です。
本問題では、こういうことでしょう。

②から①に戻ろうとするとき、②だけではバイ菌コースがまだ残っているのです。
これを…

消毒液たるc+k²≧x²+y²で、バイ菌コースを壊すのです。この条件があれば、バイ菌コースの先にあるあの式は左辺が正、右辺が負となり必ず成立しないことになります。遡ろうとすれば、②の式から①すなわち問題の条件へ戻ることが確定となったのです。バイ菌退治!!
問題を解く上では、こうやって条件→答えの逆をしたときに1本道で答え→条件に戻ってこれるかどうかを意識するのが大事です。途中で分岐点があれば、出した答えは問題の条件以外のものまで含んでしまいます。(そもそもが「○○ならば……」を示す問題なら話はまた別ですが)
本筋に戻しましょう、計算をゴリっとな!

もちろんむやみに展開してなんかいませんよ!!多少の工夫を考えながら開いています!!
まだまだぁ!!!
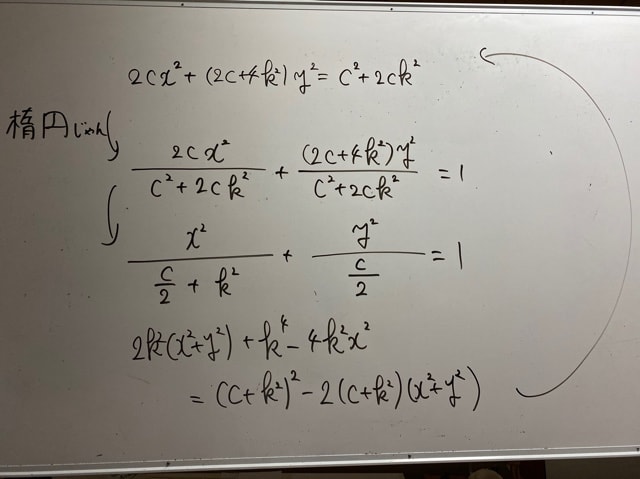
はい、計算としてはゴールインです!!
楕円でしたね!それもx軸方向に少し伸びた形のやつです。
この楕円は、さっきのc+k²≧x²+y²を満たすのでしょうか…?式で考えるのも大変なので、図を描きましょう。

青の斜線のところが、消毒液ゾーンです。この楕円は消毒液で守られているゾーンに完全に浸かっています。セーフです!
では!この楕円を答えて終いだ!!
と安心するのは少し早く…
我々は問題に与えられていない"座標"という道具を使うことで楕円を暴きました。しかし、問題では座標を使っていないため、答えるには座標に頼らない答え方をする必要があります。
そこで、定点A,Bに活躍してもらいましょう。こいつらを使って、この楕円を上手く表現できないかを考えます。
この楕円の焦点を計算してみてください。(±k,0)となりませんか??……そうつまりA,Bはこの楕円の焦点なのです!!
よっしゃ!じゃあ「軌跡はA,Bが焦点の楕円」でどうや!!!
それもまだ早いです。楕円は焦点だけで決まりません。楕円の定義にこんなものがあったのを思い出してください。
「楕円とは、平面上のある2定点から距離の和が一定となるような点の集合から作られる曲線である。」(Wikipedia様より)
そう、楕円を決めるのは2定点(焦点)と"距離の和"なのです。我々は今2つの焦点について説明しましたが、まだ距離の和がいくらになっているか??については説明していません。距離の和…どこに現れるのでしょうか……??
勉強している方なら知っているはずです。距離の和は長軸の長さに一致するんですよね!今回の問題では長軸の長さは
2√((c+2k²)/2)=√(2c+AB²)
と計算できます。
今度こそ…!
答えは
「A,Bを焦点とする、2点A,Bからのそれぞれの距離の和が√(2c+AB²)となる楕円」
(もしくは「A,Bを焦点とする、長軸の長さが√(2c+AB²)となる楕円」でも楕円は一つに定まります)
でどうでしょう!!
はーしんどかったでございます。
こんな計算をしなくても解ける解法があって、そっちの解法はなんかベクトル方程式チックなんですけど、最後の式の形に言及して「いやーこの楕円の定義と双曲線の定義の距離の和距離の差の話、たまーにポッと出てきて受験生の心を殺していくよね〜」的な話をしようと思ってたんですけど、書いてるうちに予定が完全に変わってしまいました。
皆さんも、バイ菌の侵入を防ぐことを頑張りましょう!そしていっぱい点数稼いでください!!!!(ちなみに上の僕の答案でバイ菌を防ぎ切ったとは言ってません。ミスがあれば謝罪します。)
誰向けの日記なんやこれは…
長いですが、さいごまでありがとうございました。アクセントの元気はありません。