Edith Piaf - La Vie En Rose
宗教学(初級59):大乗仏教(仏教の新たな展開) ~ 竹下雅敏 講演映像
「即非の論理」とは、般若教典の一つである「金剛般若経」における代表的な表現として、「Aは非Aにして、ゆえにAといわれる」・「Aは非Aであり、それによってまさにAである」と言われるものです
「即非の論理」とは、般若教典の一つである「金剛般若経」における代表的な表現として、「Aは非Aにして、ゆえにAといわれる」・「Aは非Aであり、それによってまさにAである」と言われるものです
現代仏教塾「日本仏教がチベット仏教に学ぶもの」Vol.3(3/6)
Discovering Buddhism Module 1 - Mind and its Potential




仏教の本質 哲学者「中村元」




仏教の本質 哲学者「中村元」
http://www.mech.cst.nihon-u.ac.jp/studies/okano/studies/phys/butsurist.html

速度(そくど、英語:velocity)は、単位時間当たりの物体の位置の変化である。
日常語としての速度(スピード、speed)は、大抵の場合一定時間あたりに進む距離のことを指す。これは [移動距離] ÷ [経過時間] で求めることができ、時速、分速などの単位が用いられる。

①変位
物体が移動したときの位置の変化を変位という。
変位は、大きさと方向・向きをもったベクトル量である。
http://ja.wikipedia.org/wiki/%E5%A4%89%E4%BD%8D
変位(へんい、英語: displacement)とは、元の位置からのずれのこと。変位の対象は、古典力学での質点の位置の「ずれ」

②速度と速さ
単位時間当たりの変位を速度という。
時間t〔s〕の間の変位が〔m〕であるとき、
この間の速度は
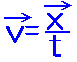
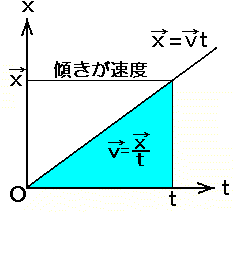

http://www.wakariyasui.sakura.ne.jp/3-1-0-0/3-1-1-1hennitosokudotokasokudo.html
より
物体が運動して位置が変わったとき、その位置の変化量を変位といいます。

運動のスピードを速度といいます。

左図の物体は途中から加速しています。加速の度合いを加速度といいます。
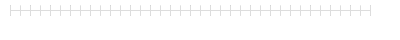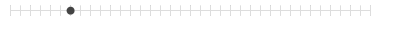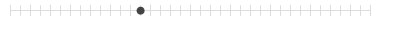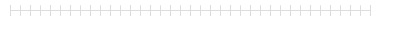
ベクトル(英: vector)
http://www.cfv21.com/math/vector.htm
より
ベクトルとは
大きさと向きを考える量をベクトルと言う。
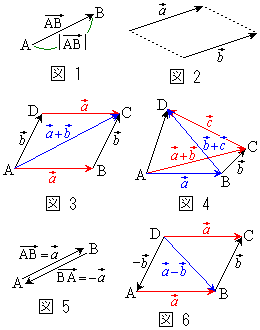
右図1のように、ベクトルは、大きさを線分の長さで示し、向きを矢印のついた線分(有向線分)で表す。
点Aと点Bを両端とする有向線分の向きがAからBに向かう向きのとき、この有向線分の表すベクトルをとする。このとき、ベクトルの出発点になっているAを始点、ベクトルの行き先になっているBを終点と言う。
ベクトルを単に1文字で、というように表すこともある。
ベクトル,の大きさを、,と表す。
2つのベクトル,があるとき、右図2のように、この両者の大きさも向きも等しいときに、2つのベクトル,が等しいと言い、と書く。
1つのベクトルを平行移動しても、大きさも向きも変化しないので、ベクトルとしても変わらない。
右図3のように3点A,B,Cがあるとき、をとの和と言い、と表す。
右図3で、四角形ABCDが平行四辺形であるとき、なので、でもある。
右図3で、,とすると、,
∴ (交換法則)
右図4で、,,として、,より、,
∴ (結合法則)
右図5で、として、をの逆ベクトルと言い、 ()と書く。となるが、は大きさ0のベクトルで向きを考えることができない。大きさ0のベクトルを零ベクトルと言い、と書く。即ち、
右図6で、をと考えることにする。,として、
kを正数として、に対して、向きを変えずにベクトルの大きさをk倍するときに、と書く。
kが負数のときには、と平行逆向きで大きさを倍とするベクトルをと書く。
のときには、ベクトルの大きさが0となるので、とする。
ベクトルの計算は、ベクトルを文字と見なして通常の文字計算と全く同様に行えばよい。
【微分・積分】
変位 →(微分)→ 速度 →(微分)→ 加速度
変位 ←(積分)← 速度 ←(積分)← 加速度
a.wikipedia.org/wiki/微分積分学
微分積分学(びぶんせきぶんがく, calculus)とは、解析学の基本的な部分を形成する数学の一分野である。微分積分学は、局所的な変化を捉える微分と局所的な量の大域的な集積を扱う積分の二本の柱からなり、分野としての範囲を確定するのは難しいが、大体多変数実数値関数の微分と積分に関わる事柄(逆関数定理やベクトル解析も)を含んでいる。
微分は、ある関数のある点での接線、或いは接平面を考える演算である。数学的に別の言い方をすると、基本的には複雑な関数を線型近似して捉えようとする考え方である。従って、微分は線型写像になる。(但し多変数関数の微分を線型写像として捉える考え方は 20世紀に入ってからのものである)。微分方程式はこの考え方の自然な延長にある。
対して積分は、幾何学的には、曲線、あるいは曲面と座標軸とに挟まれた領域の面積(体積)を求めることに相当している。ベルンハルト・リーマンは(一変数の)定積分の値を、長方形近似の極限として直接的に定義し、連続関数は積分を有することなどを証明した。彼の定義による積分をリーマン積分と呼んでいる。
微分と積分はまったく別の概念でありながら密接な関連性を持ち、一変数の場合、互いに他の逆演算としての意味を持っている
Milena Plebs y Ezequiel Farfaro - Ilusion de mi vida (HD)
Aurora Lubiz y Luciano Bastos at La Marshall in Buenos Aires (Maipo 444) - 3
Vantangofest 2011 - Nick Jones & Diana Cruz Performance 1 of 2




http://eb-cat.ds-navi.co.jp/jpn/jtekt/tech/eb/info/info1.html
軸受
http://mori.nc-net.or.jp/EokpControl?&event=TE0001
技術の森
Roberto Herrera y Silvana Capra 2008 at the Taipei Tango Festival - La Cumparsita


Indesign CS5 Tutorial: Basic Rundown of Design Tools

速度(そくど、英語:velocity)は、単位時間当たりの物体の位置の変化である。
日常語としての速度(スピード、speed)は、大抵の場合一定時間あたりに進む距離のことを指す。これは [移動距離] ÷ [経過時間] で求めることができ、時速、分速などの単位が用いられる。

①変位
物体が移動したときの位置の変化を変位という。
変位は、大きさと方向・向きをもったベクトル量である。
http://ja.wikipedia.org/wiki/%E5%A4%89%E4%BD%8D
変位(へんい、英語: displacement)とは、元の位置からのずれのこと。変位の対象は、古典力学での質点の位置の「ずれ」

②速度と速さ
単位時間当たりの変位を速度という。
時間t〔s〕の間の変位が〔m〕であるとき、
この間の速度は
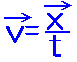


http://www.wakariyasui.sakura.ne.jp/3-1-0-0/3-1-1-1hennitosokudotokasokudo.html
より
物体が運動して位置が変わったとき、その位置の変化量を変位といいます。

運動のスピードを速度といいます。

左図の物体は途中から加速しています。加速の度合いを加速度といいます。
ベクトル(英: vector)
http://www.cfv21.com/math/vector.htm
より
ベクトルとは
大きさと向きを考える量をベクトルと言う。
右図1のように、ベクトルは、大きさを線分の長さで示し、向きを矢印のついた線分(有向線分)で表す。
点Aと点Bを両端とする有向線分の向きがAからBに向かう向きのとき、この有向線分の表すベクトルをとする。このとき、ベクトルの出発点になっているAを始点、ベクトルの行き先になっているBを終点と言う。
ベクトルを単に1文字で、というように表すこともある。
ベクトル,の大きさを、,と表す。
2つのベクトル,があるとき、右図2のように、この両者の大きさも向きも等しいときに、2つのベクトル,が等しいと言い、と書く。
1つのベクトルを平行移動しても、大きさも向きも変化しないので、ベクトルとしても変わらない。
右図3のように3点A,B,Cがあるとき、をとの和と言い、と表す。
右図3で、四角形ABCDが平行四辺形であるとき、なので、でもある。
右図3で、,とすると、,
∴ (交換法則)
右図4で、,,として、,より、,
∴ (結合法則)
右図5で、として、をの逆ベクトルと言い、 ()と書く。となるが、は大きさ0のベクトルで向きを考えることができない。大きさ0のベクトルを零ベクトルと言い、と書く。即ち、
右図6で、をと考えることにする。,として、
kを正数として、に対して、向きを変えずにベクトルの大きさをk倍するときに、と書く。
kが負数のときには、と平行逆向きで大きさを倍とするベクトルをと書く。
のときには、ベクトルの大きさが0となるので、とする。
ベクトルの計算は、ベクトルを文字と見なして通常の文字計算と全く同様に行えばよい。

【微分・積分】
変位 →(微分)→ 速度 →(微分)→ 加速度
変位 ←(積分)← 速度 ←(積分)← 加速度
a.wikipedia.org/wiki/微分積分学
微分積分学(びぶんせきぶんがく, calculus)とは、解析学の基本的な部分を形成する数学の一分野である。微分積分学は、局所的な変化を捉える微分と局所的な量の大域的な集積を扱う積分の二本の柱からなり、分野としての範囲を確定するのは難しいが、大体多変数実数値関数の微分と積分に関わる事柄(逆関数定理やベクトル解析も)を含んでいる。
微分は、ある関数のある点での接線、或いは接平面を考える演算である。数学的に別の言い方をすると、基本的には複雑な関数を線型近似して捉えようとする考え方である。従って、微分は線型写像になる。(但し多変数関数の微分を線型写像として捉える考え方は 20世紀に入ってからのものである)。微分方程式はこの考え方の自然な延長にある。
対して積分は、幾何学的には、曲線、あるいは曲面と座標軸とに挟まれた領域の面積(体積)を求めることに相当している。ベルンハルト・リーマンは(一変数の)定積分の値を、長方形近似の極限として直接的に定義し、連続関数は積分を有することなどを証明した。彼の定義による積分をリーマン積分と呼んでいる。
微分と積分はまったく別の概念でありながら密接な関連性を持ち、一変数の場合、互いに他の逆演算としての意味を持っている
Milena Plebs y Ezequiel Farfaro - Ilusion de mi vida (HD)
Aurora Lubiz y Luciano Bastos at La Marshall in Buenos Aires (Maipo 444) - 3
Vantangofest 2011 - Nick Jones & Diana Cruz Performance 1 of 2




http://eb-cat.ds-navi.co.jp/jpn/jtekt/tech/eb/info/info1.html
軸受
http://mori.nc-net.or.jp/EokpControl?&event=TE0001
技術の森
Roberto Herrera y Silvana Capra 2008 at the Taipei Tango Festival - La Cumparsita


Indesign CS5 Tutorial: Basic Rundown of Design Tools









