知恵袋: https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13308789293
▶解説
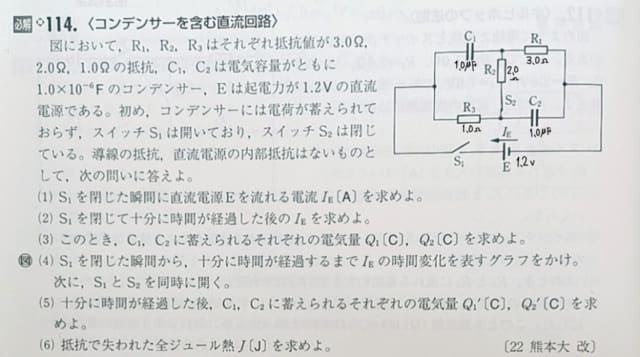
(1)、S1閉じた瞬間(経過時間t=0秒の瞬間において)t=0なので電荷は未だ動いていないのでC1,C2の極板間電位差=0v(つまりC1,C2の電圧降下=0v、つまりC1,C2は導通と同じみなせる状態)なので
電源に流れるIE=E/R2=1.2/2.0=0.6 [mA] …(答え)
(2)、S1閉じてじゅうぶん時間が経過するとコンデンサは満たん(満充電、充電完了)になりC1,C2に電流は流れなくなるので
電源に流れる電流IE=E/(R1+R2+R3)=1.2/(3.0+2.0+1.0)=1.2/6.0=0.2 [mA] …(答え)
(3)、C1は(R2+R3)と並列、C2は(R1+R2)と並列で、C1,C2には電荷Q1,Q2が溜まっているので(公式 V=Q/C より)それぞれV1=Q1/C1, V2=Q2/C2の電圧が現れており、そのV1,V2は(分圧の法則より)
V1=E×(R2+R3)/{R1+(R2+R3)}=1.2×(2.0+1.0)/(3.0+2.0+1.0)=1.2×3.0/6.0=0.6v、←向き電圧
V2=E×(R1+R2)/{(R1+R2)+R3}=1.2×(3.0+2.0)/(3.0+2.0+1.0)=1.2×5.0/6.0=1.0v、←向き電圧
ゆえにC1,C2に蓄えられる各電気量(電荷量)Q1,Q2は
Q1=C1V1=1.0×0.6=0.6μC=6.0×10^-5 [C] …(答え)
Q2=C2V2=1.0×1.0=1.0μC=1.0×10^-6 [C] …(答え)
(4)、グラフ図(未)
(5)、直前においてS2閉, S1閉でじゅうぶん時間が経過しているので(コンデンサに電流は流れないので)IE=E/(R1+R2+R3) =1.2/(3.0+2.0+1.0) =1.2/6.0 =0.2mA
ゆえに
Q1=C1×(R2+R3)×IE =1.0×(2.0+1.0)×0.2 =1.0×3.0×0.2 =0.6μC
Q2=C1×(R1+R2)×IE =1.0×(3.0+2.0)×0.2 =1.0×5.0×0.2 =1.0μC
S1,S2を同時に開きじゅうぶん時間が経過した時 (孤立部分における電荷量の保存則より)
(0.6μC+1.0μC)=C1V’+C2V’=1.0V’+1.0V’=2.0V’
V’を求めると V’=1.6/2.0=0.8v
ゆえに(電荷量の公式Q=CVより)
∴Q1’=C1V’=1.0×0.8=0.8μC=8.0×10^-7 [C] …(答え)
∴Q2’=C2V’=1.0×0.8=0.8μC=8.0×10^-7 [C] …(答え)
▶(5)の別解
S2,S1閉でじゅうぶん時間が経過すると (コンデンサに電流は流れないので 分圧の法則より)
Q1=C1×E×(R2+R3)/(R1+R2+R3) =1.0×1.2×(2.0+1.0)/(3.0+2.0+1.0) =1.0×1.2×3.0/6.0 =0.2×3.0 =0.6μC、←向き電圧0.6v
Q2=C2×E×(R1+R2)/(R1+R2+R3) =1.0×1.2×(3.0+2.0)/(3.0+2.0+1.0) =1.0×1.2×5.0/6.0 =0.2×5.0 =1.0μC、←向き電圧1.0v
S1,S2を同時に開くと (C2の電圧1.0v)−(C1の電圧0.6v)=0.4vにより 閉回路を時計回り方向に電流(➕️電荷Q)が流れ、じゅうぶん時間が経過した時 (キルヒホッフの第2法則より) 0.4v=Q/C1+Q/C2 =Q/1.0+Q/1.0 =2Q/1.0
Qを求めると Q=0.4/(2/1.0)=0.2μC
この0.2μCの電荷量が 閉回路を時計回り方向へ流れるので
C1に溜る電荷量Q1’=0.6+0.2=0.8μC=8.0×10^-7 [C] …(答え)
C2に残る電荷量Q2’=1.0−0.2=0.8μC=8.0×10^-7 [C] …(答え)















