▶第3の解き方
S1閉じ定常状態後のQ1,Q2は
(同じ電荷量Qなので、キルヒホッフの第2法則、電荷の公式V=Q/Cより)
30=V1+V2=Q/C1+Q/C2=Q×(1/1+1/2)=2Q/3より
Qを求めるとQ=Q1=Q2=30/(3/2)=20[μC]
S1開き、S2閉じ定常状態後のQ2,Q3は
(C2,C3は同じ電圧V[V]で定常状態になるので、孤立部分における電荷の保存則、電荷の公式Q=CVより)
Q=20=Q2+Q3=C2V+C3V=(2×V)+(3×V)=5×V [μC]より
(公式V=Q/Cを使ってVを求めると)V=20/5=4[V]
∴Q2=2×4⁼8μC、∴Q3=3×4=12μC
S2開き、S1閉じ定常状態後のQ1,Q2を求めると
(S1閉じる直前のC1,C2の電圧20V,4V
なので30Vとの電位差は) 30-20-4=6V
この6VによりC1,C2に新たに充電される電荷をQ’とすると
Q’=1×6×2/(1+2)=4[μC] (又は Q’=2×6×1/(1+2)=4[μC])
(この時、C1,C2は直列だから、この電荷量Q’=4μCが新たに追加されるので)
∴Q1=20+4=24[μC]
∴Q2=8+4=12[μC]
↑
こんな解法もありますよ、(^o^)ノ
▼つなぎ替え2

(1)、
- 賢者の解答だったので備忘録として残します。
【知恵袋】https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14290921579

▶nura-rihyonさんの解答より
対称性から図2右上の電源による電流は0
真ん中の電源から流れ出る電流はIbcで、
半分がbc間に流れるのでIbc/2
それぞれと元の電流を足して3Ibc/2
▶nura-rihyonさんの解答を踏襲すると下図

▶賢者の解答だったので備忘録として残します。
知恵袋:https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q10291893330
【問題】図(a)から図(b)の回路に変換する際、R1を流れるI1とR2を流れるI2が図(a)と図(b)でそれぞれ変化しないようにしたい。 これを達成できるExとRxをそれぞれE、R3およびR4を用いて示せ。

≫fried_turnipさんの回答を元にした、私なりの解答です↓
▼等価性より(相反性?) 図(a)、図(b)においてVa=Vbが成立する為には、図1=図2であればよい。

▼ミルマンの定理で解く R1を流れるI1とR2を流れるI2が図(a)と図(b)でそれぞれ変化しない様にしたい。と云う事はVa=Vbである必要がある。つまりVa=Vbが条件なので、この条件を下に解析し易い様に変形すると…

▼等価性 Va=Vbなら、回路の等価性より (a-3)=(b-2) と云える。つまり(a-3)と(b-1)を入れ替えて元の回路に戻してもI1,I2に影響を与える事がないので(a-3)と(b-1)は等価交換できる、と云う事です。

▶電気回路の等電位間(電位差=0)に電流は流れない。故に、等電位間は
①、切り離しても
②、短絡しても
③、抵抗など繋いでも
その等電位の間に電流は流れない。
▶ブリッジ回路が平衡状態の時
▶事例
知恵袋➜ https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13291870063
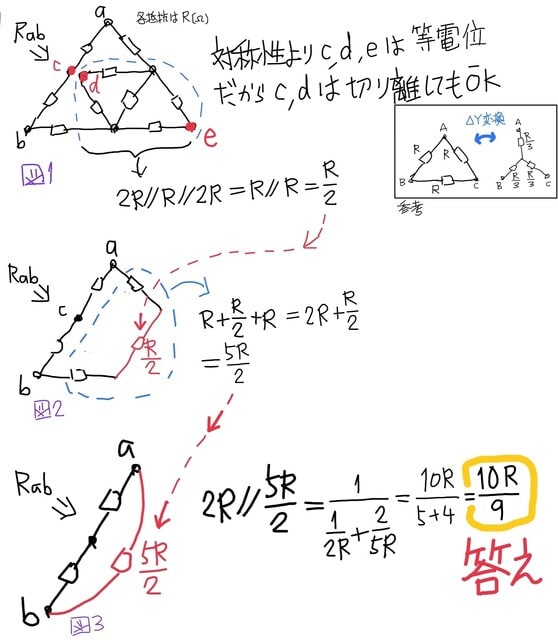
参考:ΔY変換、YΔ変換
知恵袋での質問者はΔY変換による回答が欲しいのだろーと思われるのですが、ここでは計算がも最も楽かなーと思われる解法を提示します。 この回路はceを中心軸として対称な回路なのでce軸を中心に180°回転すると、元の回路と全く同じです。 ゆえに対称性より下図の様に等価変換して解けます。