自然界に現れる数字の頻度に関してベンフォードの法則(ウィキペディアの説明を参照してください)というのがあるそうですが、それを会計数値に適用して、不正発見に役立てる方法を説明した記事。エクセルを使ってできるそうです。
コンピュータの乱数で作った数字や、キーボードの数字キーを適当に打って入力した数字がデータの中にあると、この法則に当てはまらないので、異常だとわかるそうです。また、例えば、500ドル以上とか1000ドル以上を承認を要する小切手金額としている場合には、不正があれば、4や9がベンフォードの法則による頻度よりも多く出現すると考えられます。
ベンフォードの法則を使った分析だけで、不正の有無を決定できるわけではありません。さらに、分析的手続を行ったり、内部統制を点検したりする必要があります。そもそも、不正がなくても、この法則が当てはまらないような場合もあります。
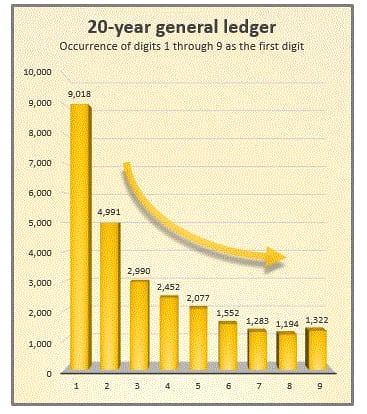
この記事の筆者の総勘定元帳データを分析した結果。たしかに、法則にほぼ当てはまっています。
↓
ベンフォードの法則(ウィキペディア)
「ベンフォードの法則(ベンフォードのほうそく、英語: Benford's law)は、自然界に出てくる多くの(全てのではない)数値の最初の桁の分布が一様ではない、ある特定のものになっているというものである。この法則によれば、最初の桁が1である確率はほぼ3分の1にも達し、大きな数値ほど最初の桁に現れる確率は小さくなり、9になると最初の桁に現れる確率は20分の1よりも小さくなる。数理的には、数値が対数的に分布しているときは常に最初の桁の数値がこのような分布で出現する。...
この直感に反するような結果は、電気料金の請求書、住所の番地、株価、人口の数値、死亡率、川の長さ、物理・数学定数、冪乗則で表現されるような過程(自然界ではとても一般的なものである)など、様々な種類の数値の集合に適用できることがわかっている。」
この記事にもベンフォードの法則が登場しています。
↓
デジタル分析入門(タビスランド)
