Quaternion の回転式の展開[Blender 3DCG]の続き
今回は肩のねじれを防ぐ Y=0 の Quaternion(W,X,0,Z) を求める。
もう少し具体的に説明すると
肩を y≠0 の Quaternion(w,x,y,z)で回転させた時と
肩を Y=0 の Quaternion(W,X,0,Z)で回転させた時で、
腕の方向が一致するような W,X,Z を w,x,y,z から求める。
( 英文字の小文字と大文字の違いに注意 )
腕の方向は、肩の Bone の Y軸方向(0,1,0) と同じなので、
(0,1,0)を回転させた結果が一致する場合について考える。
前回求めた Quaternion(w,x,y,z) の回転式の展開結果に
(p,q,r)=(0,1,0) を代入すると、qの項目のみ残るので以下となる。
(w,x,y,z)(0,0,1,0)(w,-x,-y,-z)=(0,2xy-2wz,ww-xx+yy-zz,2yz+2wx ) …①
同様に Quaternion(W,X,0,Z) の回転結果は以下となる。
(W,X,0,Z)(0,0,1,0)(W,-X, 0,-Z)=(0, -2WZ,WW-XX -ZZ, 2WX ) …②
②=①なので
-2WZ = 2xy-2wz …③
WW-XX-ZZ = ww-xx+yy-zz …④
2WX = 2yz+2wx …⑤
回転に用いる Quaternion は各項目の2乗和が 1 になるので
WW+XX +ZZ-1=0 …⑥
ww+xx+yy+zz-1=0 …⑦
④左と⑥より
WW-XX-ZZ
= WW-XX-ZZ + WW+XX+ZZ-1
= 2WW-1 …④左'
④右と⑦より
ww-xx+yy-zz
= ww-xx+yy-zz + ww+xx+yy+zz-1
= 2ww+2yy-1 …④右'
④左'=④右'を解き W を得る。( ^ はべき乗 )
2WW-1=2ww+2yy-1
2WW =2ww+2yy
WW = ww+ yy
W = (ww+ yy)^0.5 … ⑧
次に ③ と W から Z を得る。
-2WZ = 2xy-2wz
2WZ = 2wz-2xy
WZ = wz- xy
Z = (wz- xy)/W = (wz- xy)/((ww+yy)^0.5)
次に ⑤ と W から X を得る。
2WX = 2yz+2wx
WX = yz+ wx
X = (yz+ wx)/W = (yz+wx)/((ww+yy)^0.5)
まとめると以下となる。
( X の wx と yz の順は Z に合わせて入れ替えた。)
W= (ww+yy)^0.5
X=(wx+yz)/((ww+yy)^0.5)
Z=(wz-xy)/((ww+yy)^0.5)
Blenderのpythonで、アクティブなボーンのQuaternionのYを0にするコードは以下。
w,x,y,z = bpy.context.active_pose_bone.rotation_quaternion
W = (w*w+y*y)**0.5
X = (w*x+y*z)/((w*w+y*y)**0.5)
Y = 0.0
Z = (w*z-x*y)/((w*w+y*y)**0.5)
bpy.context.active_pose_bone.rotation_quaternion = Quaternion((W,X,Y,Z))
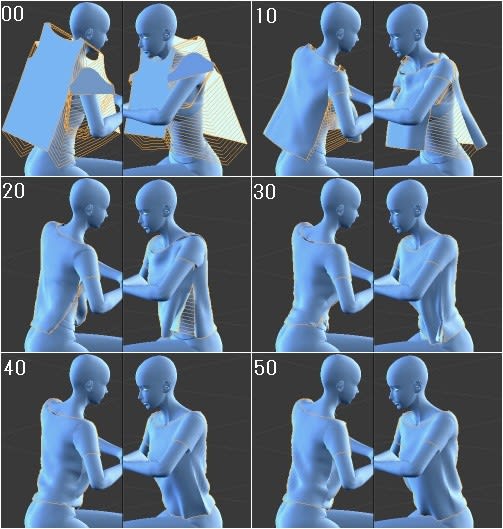
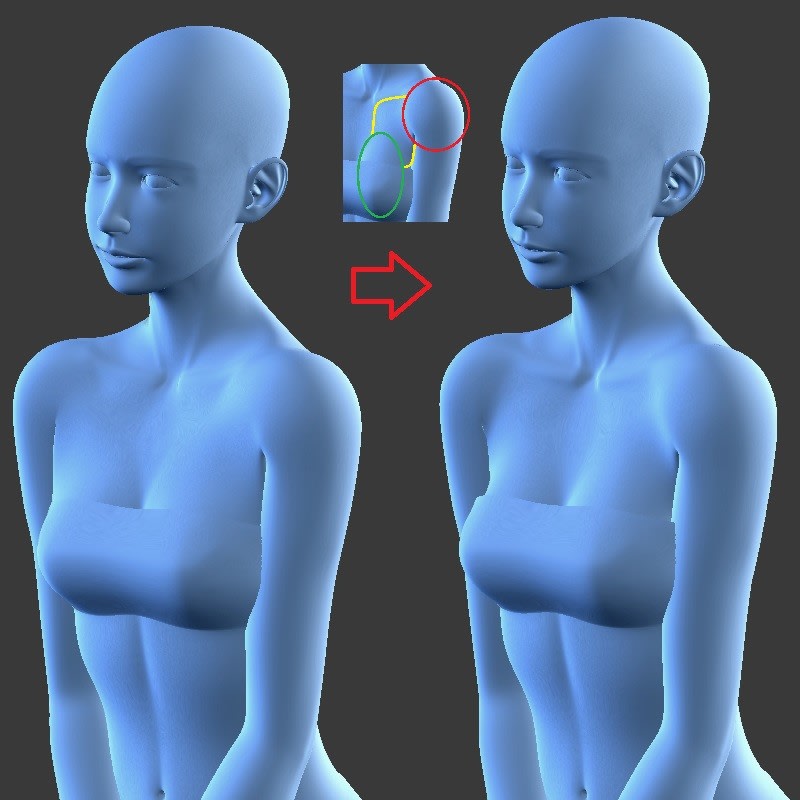
これを使用したのが
肩のポージングは難しい[Blender 3DCG] と 以下の絵。

わきの下の皺に悩まされずにポージングできるようになった。
「これで肩だしにも自信が持てます!」
(なんだかエステの体験談みたいだ^^;)
最後に…
T字型の基本姿勢(腕を真横に伸ばした基本姿勢)でしか試したことがないため、
その他の基本姿勢でうまくいくかどうかは定かではない^^;