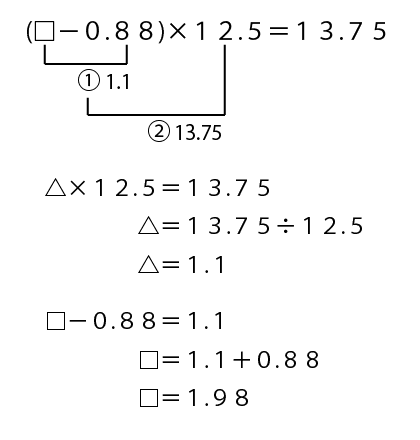
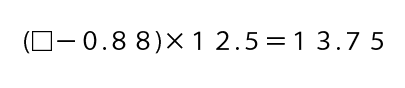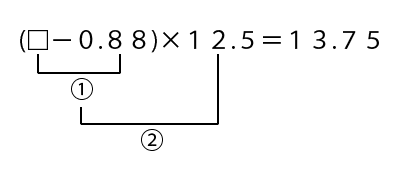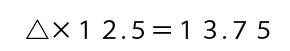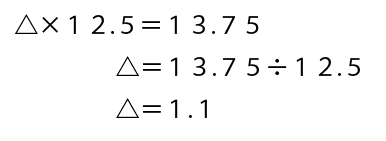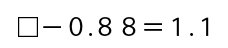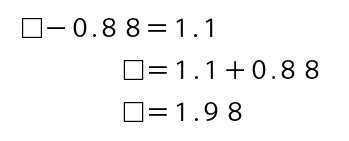前回に引き続き、以前紹介したこちら→逆算の計算の仕方 だいぶ複雑なもの を別のやり方で解いていきます。
同じこの計算式で解いていきましょう。
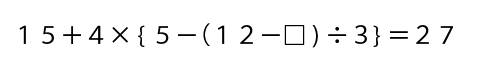
面倒臭そうですね!
まず計算の順序を書きます。
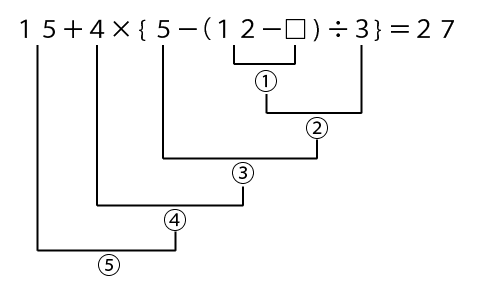
一番目の計算、①に□があって解けないので、最後の⑤から解いていきます。
⑤は最後の計算ですね。よって答えは27ですので、⑤の横に書き込みます。
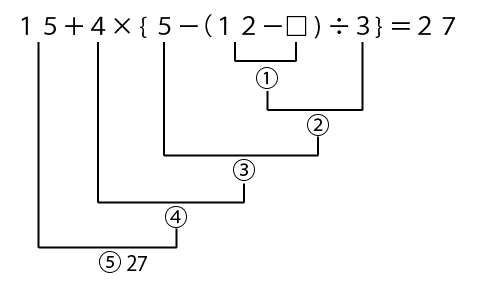
こんな感じ。
15+「④の計算の答え」が27になるということですね。④の計算の答えはわからないので△とおくと
こういう計算式ができます。
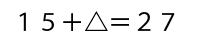
基本の逆算の形ですので、このまま解いていきましょう。
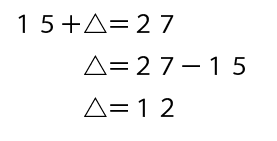
△、つまり④の計算の答えが12とわかりました!
元の式の④のところに書き込みましょう。
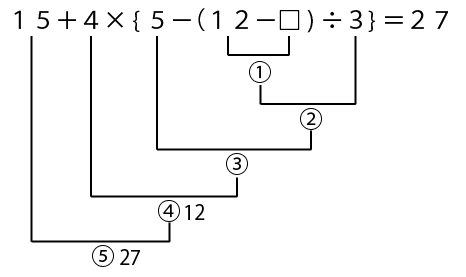
こんな感じですね。
4×「③の計算の答え」が12、ということがわかりましたので、次は③の計算の答えを△と置いて
式を立てます。
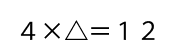
こうなりますね。解いていきましょう。
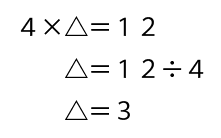
△、つまり③の計算の答えが3とわかりましたので、これも元の式に書き込みます。
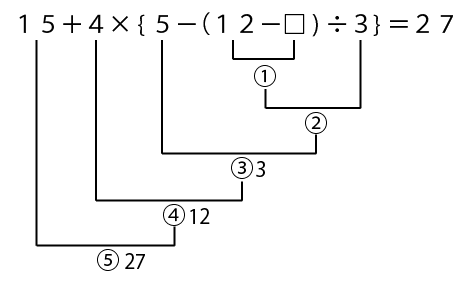
だいぶぜまってきましたね!
次は5−「②の計算の答え」が3とわかりましたので、同じように②の計算の答えを△と置いて
式を立てて計算をしましょう。
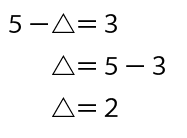
こうですね!
②の計算の答えが2とわかりましたので、元の式に書き込みます。
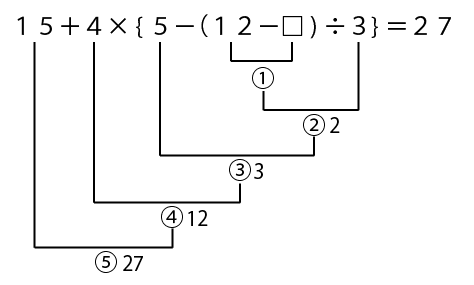
あと少しですね!
「①の計算の答え」÷3の答えが2と分かりましたので、①の計算の答えを△と置き、式を立てて計算をしましょう。
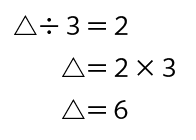
△、つまり①の計算の答えが6とわかりました!
元の式に書き込みましょう。
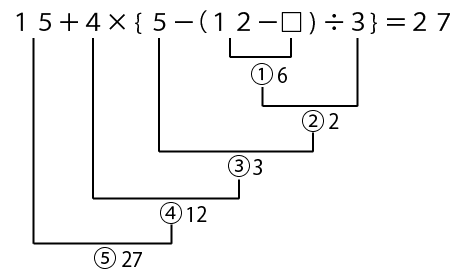
ということで、とうとう最後の①の計算の答えがわかったので、式を立てて計算をします。
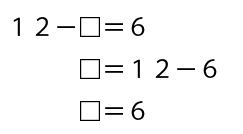
□に当てはまる数は6でした!
解いた全体像はこんな感じになりました。
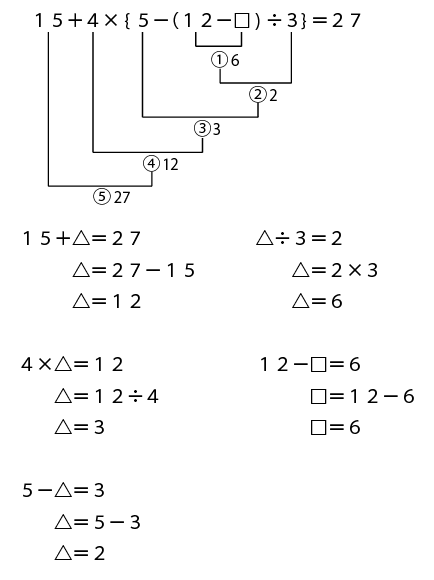
このやり方で解くときのポイントは、出した答えを元の式に書き込んでいくことでしょうか。
どちらのやり方でもやっていることは同じなのですが、
大きい□、という考え方がちょっとなじまない人はこちらのやり方のほうがやりやすいようです。
同じこの計算式で解いていきましょう。
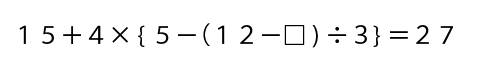
面倒臭そうですね!
まず計算の順序を書きます。

一番目の計算、①に□があって解けないので、最後の⑤から解いていきます。
⑤は最後の計算ですね。よって答えは27ですので、⑤の横に書き込みます。

こんな感じ。
15+「④の計算の答え」が27になるということですね。④の計算の答えはわからないので△とおくと
こういう計算式ができます。
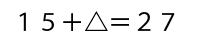
基本の逆算の形ですので、このまま解いていきましょう。
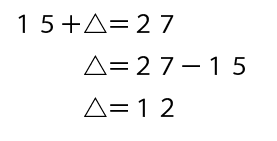
△、つまり④の計算の答えが12とわかりました!
元の式の④のところに書き込みましょう。

こんな感じですね。
4×「③の計算の答え」が12、ということがわかりましたので、次は③の計算の答えを△と置いて
式を立てます。
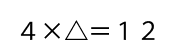
こうなりますね。解いていきましょう。
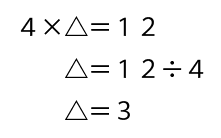
△、つまり③の計算の答えが3とわかりましたので、これも元の式に書き込みます。

だいぶぜまってきましたね!
次は5−「②の計算の答え」が3とわかりましたので、同じように②の計算の答えを△と置いて
式を立てて計算をしましょう。
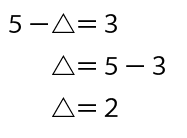
こうですね!
②の計算の答えが2とわかりましたので、元の式に書き込みます。

あと少しですね!
「①の計算の答え」÷3の答えが2と分かりましたので、①の計算の答えを△と置き、式を立てて計算をしましょう。
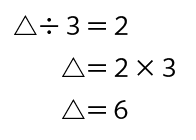
△、つまり①の計算の答えが6とわかりました!
元の式に書き込みましょう。

ということで、とうとう最後の①の計算の答えがわかったので、式を立てて計算をします。
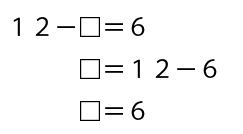
□に当てはまる数は6でした!
解いた全体像はこんな感じになりました。

このやり方で解くときのポイントは、出した答えを元の式に書き込んでいくことでしょうか。
どちらのやり方でもやっていることは同じなのですが、
大きい□、という考え方がちょっとなじまない人はこちらのやり方のほうがやりやすいようです。