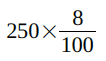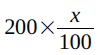前回出した例題を解いてみましょう。
例題
8%の食塩水があります。ここに3%の食塩水を200g混ぜると6%の食塩水になりました。
8%の食塩水は何gありましたか。
方程式は、求めるものをxとしてたてるのでしたね。
8%の食塩水の重さをx gとします。
食塩水の問題は、溶けている食塩の重さの式を考えるとよいので、
この問題ですと
8%の食塩水に溶けている食塩の重さ+3%の食塩水に溶けている食塩の重さ=6%の食塩水に溶けている食塩の重さ
となりますね。
それぞれを式に表しましょう。
溶けている食塩の重さは食塩水全体の重さ×濃度
でしたね。
8%の食塩水に溶けている食塩の重さは
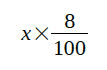
3%の食塩水に溶けている食塩の重さは

6%の食塩水に溶けている食塩の重さは

よって方程式は

となります。
計算しましょう。
両辺に100をかけて整数の式にしてから計算します。
8x+200×3=(x+200)×6
8x+600=6x+1200
8x−6x=1200−600
2x=600
x=300
ということで、8%の食塩水の重さは300gでした!
食塩水の問題は、
溶けている食塩の重さに目をつける
溶けている食塩の重さは食塩水全体の重さ×濃度
を理解していれば、
0%の食塩水300gと1%の食塩水を何gかをよく混ぜて、そこに食塩を20g入れ、さらにそこから水を70g蒸発させたら6%の食塩水になりました。
1%の食塩水は何gですか。
5%の食塩水に食塩を50g入れて、そのあと水を200g加え、さ らに1%の食塩水を400g加えてよくかき混ぜたら、6%の食塩水ができました。
5%の食塩水は何gですか。
などのややこしい問題も楽勝ですね!
中1の人は、たくさんの問題にあたって、基礎をしっかりと固めましょう!
例題
8%の食塩水があります。ここに3%の食塩水を200g混ぜると6%の食塩水になりました。
8%の食塩水は何gありましたか。
方程式は、求めるものをxとしてたてるのでしたね。
8%の食塩水の重さをx gとします。
食塩水の問題は、溶けている食塩の重さの式を考えるとよいので、
この問題ですと
8%の食塩水に溶けている食塩の重さ+3%の食塩水に溶けている食塩の重さ=6%の食塩水に溶けている食塩の重さ
となりますね。
それぞれを式に表しましょう。
溶けている食塩の重さは食塩水全体の重さ×濃度
でしたね。
8%の食塩水に溶けている食塩の重さは
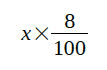
3%の食塩水に溶けている食塩の重さは

6%の食塩水に溶けている食塩の重さは

よって方程式は

となります。
計算しましょう。
両辺に100をかけて整数の式にしてから計算します。
8x+200×3=(x+200)×6
8x+600=6x+1200
8x−6x=1200−600
2x=600
x=300
ということで、8%の食塩水の重さは300gでした!
食塩水の問題は、
溶けている食塩の重さに目をつける
溶けている食塩の重さは食塩水全体の重さ×濃度
を理解していれば、
0%の食塩水300gと1%の食塩水を何gかをよく混ぜて、そこに食塩を20g入れ、さらにそこから水を70g蒸発させたら6%の食塩水になりました。
1%の食塩水は何gですか。
5%の食塩水に食塩を50g入れて、そのあと水を200g加え、さ らに1%の食塩水を400g加えてよくかき混ぜたら、6%の食塩水ができました。
5%の食塩水は何gですか。
などのややこしい問題も楽勝ですね!
中1の人は、たくさんの問題にあたって、基礎をしっかりと固めましょう!