*中和の考え方1・2はこちら→1 2
中和の問題にはグラフがよく出て来ます。
例えばこんな感じ。
問:次のグラフは、ある濃さの水酸化ナトリウム水溶液と塩酸を混ぜ合わせて
完全に中和したときの体積を表したグラフです。

グラフを見るときは、
①何を表しているグラフなのか
②縦軸と横軸はそれぞれ何か
③縦軸と横軸の単位はそれぞれ何か
④縦軸と横軸の目盛りはそれぞれいくつか
を、まず読み取ります。
当たり前のことなんですが、見ていない生徒は実は非常に多いです。
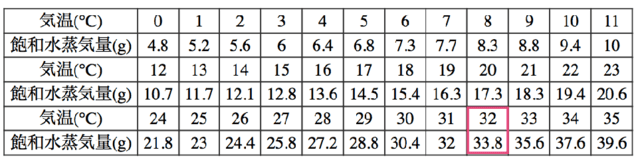
このグラフの場合、
①ある濃さの水酸化ナトリウム水溶液と塩酸が中和するときのそれぞれの体積
②縦軸は水酸化ナトリウム水溶液の体積、横軸は塩酸の体積
③縦軸、横軸ともに㎤
④縦軸、横軸ともに1目盛5㎤
ですね。
そしてグラフを読み取るのですが、目盛りの線とグラフの線が
ちょうどぴったり合っているところを見ます。
このグラフでしたら、

ここか

ここですね。
下のグラフの方が見やすいので、こちらで読み取りますと

水酸化ナトリウム水溶液は40㎤、

塩酸は30㎤
で混ぜ合わせると中和することが分かります。
つまりこの問題文の濃さの水酸化ナトリウム水溶液と塩酸は
40:30=4:3の体積で混ぜ合わせると中和することが
グラフから読み取れました。
読み取れたところで、教え子が間違えてしまった問題がこちらです。
塩酸の濃さはそのままで水酸化ナトリウム水溶液の濃さを2倍にすると、
グラフはどのようになりますか。下のア〜エから選び、記号で答えなさい。

教え子は
元の水溶液は水酸化ナトリウム:塩酸=4:3で中和していて
水酸化ナトリウム水溶液を2倍の濃さにしたから、4×2=8で、8:3になるから
水酸化ナトリウム水溶液と塩酸が8:3になっているのはイだから答えはイ
としました。
うん、2倍っていうのは濃さが2倍なんだよ、と言ってもピンときていません。
これは中和の意味があんまり頭に入っていないな、ということで
もう一度中和の考え方をやり直しました。
濃さが2倍とは、大雑把に言えば、同じ量の水に溶けている水酸化ナトリウムの量が2倍、
ということですね。
そうすると、中和の相手の塩化水素の量も2倍でないと中和できません。
元の濃さで中和していた4:3の体積ですと、塩酸に溶けている塩化水素の量が
足りないということになります。
ということは、塩酸の量を2倍にしてやれば、溶けている水酸化ナトリウムの量と塩化水素の量は
ちょうどぴったり合いますね。
ですので式は 3×2=6 となり、4:6=2:3の体積で中和することがわかります。
水酸化ナトリウム水溶液:塩酸=2:3 になっているグラフはウですので
答えはウとなります。
問題をたくさんやっていくと、グラフが出てきたらここの部分を使えばいい、
計算はこういう計算式に数字を当てはめてやればいい、というような所謂
「やり方」だけをマスターしてしまいがちですが
やはり基礎をしっかりと理解した方が後々困らなくてすみますね。
中和の問題にはグラフがよく出て来ます。
例えばこんな感じ。
問:次のグラフは、ある濃さの水酸化ナトリウム水溶液と塩酸を混ぜ合わせて
完全に中和したときの体積を表したグラフです。

グラフを見るときは、
①何を表しているグラフなのか
②縦軸と横軸はそれぞれ何か
③縦軸と横軸の単位はそれぞれ何か
④縦軸と横軸の目盛りはそれぞれいくつか
を、まず読み取ります。
当たり前のことなんですが、見ていない生徒は実は非常に多いです。
このグラフの場合、
①ある濃さの水酸化ナトリウム水溶液と塩酸が中和するときのそれぞれの体積
②縦軸は水酸化ナトリウム水溶液の体積、横軸は塩酸の体積
③縦軸、横軸ともに㎤
④縦軸、横軸ともに1目盛5㎤
ですね。
そしてグラフを読み取るのですが、目盛りの線とグラフの線が
ちょうどぴったり合っているところを見ます。
このグラフでしたら、

ここか

ここですね。
下のグラフの方が見やすいので、こちらで読み取りますと

水酸化ナトリウム水溶液は40㎤、

塩酸は30㎤
で混ぜ合わせると中和することが分かります。
つまりこの問題文の濃さの水酸化ナトリウム水溶液と塩酸は
40:30=4:3の体積で混ぜ合わせると中和することが
グラフから読み取れました。
読み取れたところで、教え子が間違えてしまった問題がこちらです。
塩酸の濃さはそのままで水酸化ナトリウム水溶液の濃さを2倍にすると、
グラフはどのようになりますか。下のア〜エから選び、記号で答えなさい。

教え子は
元の水溶液は水酸化ナトリウム:塩酸=4:3で中和していて
水酸化ナトリウム水溶液を2倍の濃さにしたから、4×2=8で、8:3になるから
水酸化ナトリウム水溶液と塩酸が8:3になっているのはイだから答えはイ
としました。
うん、2倍っていうのは濃さが2倍なんだよ、と言ってもピンときていません。
これは中和の意味があんまり頭に入っていないな、ということで
もう一度中和の考え方をやり直しました。
濃さが2倍とは、大雑把に言えば、同じ量の水に溶けている水酸化ナトリウムの量が2倍、
ということですね。
そうすると、中和の相手の塩化水素の量も2倍でないと中和できません。
元の濃さで中和していた4:3の体積ですと、塩酸に溶けている塩化水素の量が
足りないということになります。
ということは、塩酸の量を2倍にしてやれば、溶けている水酸化ナトリウムの量と塩化水素の量は
ちょうどぴったり合いますね。
ですので式は 3×2=6 となり、4:6=2:3の体積で中和することがわかります。
水酸化ナトリウム水溶液:塩酸=2:3 になっているグラフはウですので
答えはウとなります。
問題をたくさんやっていくと、グラフが出てきたらここの部分を使えばいい、
計算はこういう計算式に数字を当てはめてやればいい、というような所謂
「やり方」だけをマスターしてしまいがちですが
やはり基礎をしっかりと理解した方が後々困らなくてすみますね。











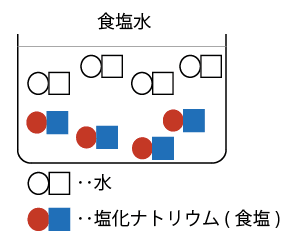
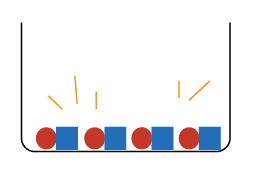



 と
と
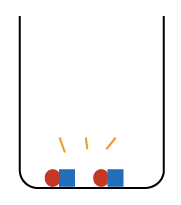

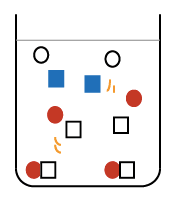
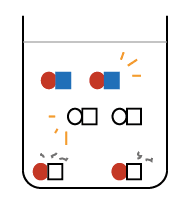






 の数で、濃さが変わると考えてください。
の数で、濃さが変わると考えてください。



 と
と