ソースをGItHubで公開しましたので、中身について詳しく見てみたい方はそちらのcalc.asmをご覧下さい。モニタープログラム、通信、I/O周りで1KB、電卓部分が1KBぐらいになってます。
ちなみに、Intel 4004 — 50th Anniversary Projectには、Busicom 141-PFのプログラムをリバースエンジニアリングしたソースコード(Busicom-141PF-Calculator_asm_rel-1-0-1.txt)があり、それを見るとJIN(レジスタ値へのジャンプ)命令を駆使して疑似命令(pseudo instruction code)で書いたプログラムを実行するという手法が使われています。この手法は、メモリ効率やデバッグ効率等いろいろ利点がありそうなのですが、事前に疑似命令の設計をきちんとやる必要がありそうです。
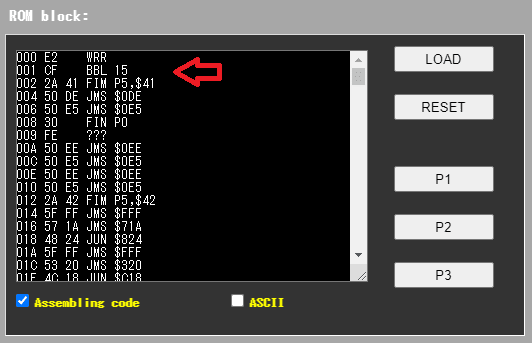
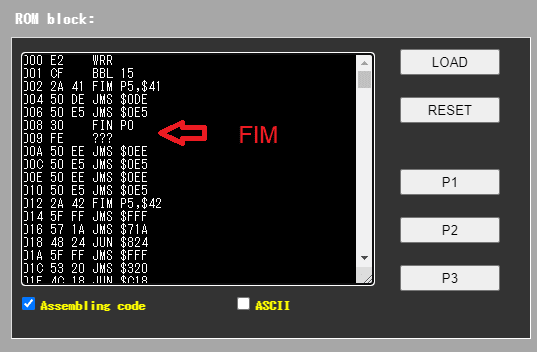
今回はとりあえず作ってみようと書き始めたので、ネイティブな命令を並べてJMS(サブルーチンコール)で呼ぶという普通の書き方をしています。
苦労した点がいろいろありました。主なのは、
(a) スタックが4段しか無い
(b) CPUのレジスタが4bit x 16個(8bit x8個で使うことが多い)しかないのに退避が出来ない
(c) 条件分岐が同一ページ(256byte単位)内にしか飛べない
あたりかな。
(a)のせいで、サブルーチンがちょっと深くなるだけで暴走します。メインルーチンから3段までしかサブルーチンを呼べません。サブルーチンコールをジャンプで置き替えが可能であれば置き替える等で対処しました。
(b)については、サブルーチンを呼んだときに壊されるレジスタを常に意識する。
(c)については、かたまり毎にorg命令で明示的に配置する。ページ境界には分岐しないルーチンを置く。
というようなことを意識しながらプログラムを書きました。
電卓の作成における主な作業項目と労力の割合はこんな感じ。
(1) 数値表現方法の検討 (30%)
(2) 入力処理 (20%)
(3) 加算 (25%)
(4) 減算(0%)
(5) 乗算 (10%)
(6) 除算 (10%)
(7) 平方根 (5%)
順を追って説明します。
まず「(1)数値表現方法の検討」です。プログラム自体のコーディング作業はありませんが、それより面倒な仕様検討の作業です。今回はCPUの能力、命令セット、メモリ等が強い制約条件になっているので、それらを考慮して実装しやすさ優先で決めました。
まずは整数だけで我慢するか、固定小数点にするか、浮動小数点にするかというあたりですが、簡易的な浮動小数点にしました。
整数と固定小数点はほぼ同じことです。クルタ式計算機やタイガー計算機のような機械式計算機ぐらいの計算能力が実現できます。
浮動小数点というと一見難しそうですが、単に整数相当の仮数部に、桁数を表わす指数部をつけたものです。加減算時の桁数揃え、乗除算時に指数部の加減算が付くぐらいなので、実はそんなに難しくありません。
フォーマットはIEEE 754風にしようかと思ったのですが、bit演算どころか論理演算の命令も無い4004には実装しにくそうなのでやめました。
内部表現を10進数にするか、2進(16進)数にするかという選択肢は10進数(BCD)にしました。4004は電卓を作るために開発されただけあって、10進数の加減算のための補正命令(DAA, TCS)があったので。入出力時に10進←→2進の変換が不要になるというメリットがあります。
調べていたら、IntelのMCS-4アセンブラマニュアルに浮動小数点に関する記述を発見。

これ使えるじゃん!と思って作り始めたのですが、指数部分が符号付き2桁なのは地味に面倒。あと、この図では上位の桁が左(若番)のキャラクタに格納されていますが、逆の方がいいです。別のページにある整数の格納の図では下位の桁が左になっていて、整数の加減算のサンプルコードも示されています。これ、マニュアル書いた人も浮動小数が表現できるよと示しただけで、実装してなかったんじゃないかなあ。
指数部は4bitの符号無し整数にしました。昔の「可変長の小数はあるけど指数表示は無い」電卓が扱うレベルの数値が表現できます。実装したフォーマットとRAMレジスタへの格納方法はこんな感じ。
(+/-)D.DDDDDDDDDDDDDDD*(10^E)
データキャラクタ0~15: 各4bitのBCD, D15が上位桁、D0が下位桁。
ステータスキャラクタ0: 指数部(4bit, 0~14) (15になるとオーバーフロー)
ステータスキャラクタ1: 符号(0000:+, 1111:-) 符号に4ビット使う贅沢仕様(CMA命令で反転したいので)
ステータスキャラクタ2: エラーフラグ(bit0: overflow bit1: divide by zero, 2bit未使用)
D15は普段は0になるように正規化しておきます。これは、掛け算や足し算の計算中の桁上がりで数字を入れる余地を残しておくためです。
最初は、「(+/-).DDDDDDDDDDDDDDDD*(10^E)」のようにしていたのですが、桁上がり時の処理が面倒だったので、1桁犠牲にしてプログラムを簡略化しました。
次に「(2)入力処理」です。入力された数値や演算子の処理です。
演算子の入力方法は逆ポーランド方式を採用しました。入力された次点で演算ルーチンに飛べばいいので実装が楽なのです。
数値入力は一見簡単なのですが、冒頭の「0」の扱いや、桁のオーバーフロー、「.」が複数回押されても無視する、演算直後の数値入力時にスタックに自動的に自動的にプッシュする、等々、例外的な事項をいろいろ気にしなくてはならなくて雑多に面倒でした。CPUのレジスタに余裕が無いこともあり、フラグやレジスタをどこにどう割り当てるかというあたりで結構と苦労しました。
いよいよ演算ルーチンです。まずは「(3)加算」。
数値表現の方法に、符号は使わずにマイナスの数は補数にするという方法があります。そうすると、加算、減算、負の数の加減算も全部単に加算するだけで済むので簡単です。しかしながら、出力時や乗除算時に「正数+符号」への変換が必要で、そちらが面倒になります。
今回は「符号+BCD16桁」という内部表現を採用したので、加算時には符号による場合分けが必要になります。
X+Yの計算の概略フローは次の通り。
・XとYの符号を調べる
→符号が同じなら|X|+|Y|を計算して符号はそのまま。
→符号が違う場合は、max(|X|, |Y|) - min(|X|, |Y|)を計算して符号は絶対値が大きい方の符号にする。
・仮数部の加減算を、大きい方の桁数にあわせてから(小さい方をシフトしてから)行う。
・仮数部が0でない場合、D15=0, D14!=0になるように仮数部と指数部を正規化する。
以上です。
BCD16桁の加算は下記のような簡単なループで実行できます。
ADD_FRA_LOOP:
SRC P7
RDM
SRC P6
ADM
DAA
WRM
INC R13
ISZ R15, ADD_FRA_LOOP
ADD_FRA_EXIT:
BBL 0 BCD 16桁の減算はこんな感じ。
SUB_FRA_LOOP:
TCS
SRC P7
SBM
CLC
SRC P6
ADM
DAA
WRM
INC R13
ISZ R15, SUB_FRA_LOOP
BBL 0これで加算ができました。「(4)減算」はX-Y = X + (-Y)なので上記ルーチンを呼ぶだけです。
次は「(5)乗算」。下記のように、被乗数(Y)を右にシフト(10で割ることに相当)しながら乗数(M(Xのコピー))の各桁(1桁)の数字を掛け算して結果レジスタ(X)に加算していきます。(実装の都合で、M=X*Yではなく、X=Y*Mになっています)。1桁の掛け算は足し算のループで実行します。機械式計算機で掛け算するときと同じですね。
本当は倍の長さの桁を用意しないといけないのでしょうが、下の方の桁はどうせ捨てられるのでサボっています。ソースに書いたコメントを貼っておきます。(これで伝わるかなあ)
;;; sum up folloings and store to FRA_X
;;; FRA_Y
;;; 0EDCBA9876543210 * 0 FRA_M(=FRA_X)
;;; 0EDCBA987654321 * E
;;; 0EDCBA98765432 * D
;;; 0EDCBA9876543 * C
;;; 0EDCBA987654 * B
;;; 0EDCBA98765 * A
;;; 0EDCBA9876 * 9
;;; 0EDCBA987 * 8
;;; 0EDCBA98 * 7
;;; 0EDCBA9 * 6
;;; 0EDCBA * 5
;;; 0EDCB * 4
;;; 0EDC * 3
;;; 0ED * 2
;;; 0E * 1
;;; 0 * 0次は「(6) 除算」です。基本的に筆算で割り算するときと同じです。仮数部の桁をあわせてから、引けるかどうか大小比較して引ければ引くということを繰り返し、何回引けたかを結果レジスタに記録していきます。引けなくなったら除数を右にシフトして次の桁に進みます。
最初に実装してみたら、結果の桁が"A"(10)になってしまうことが稀に発生して謎だったのですが、100/109で引けなくなったときに次の桁では100/10のように除数が丸められてしまうのが原因でした。とりあえず、10回以上引くことがないように乱暴に対処しましたが、ちゃんとした電卓を作るときはこういうところをちゃんと処理しなきゃいけないんだろうなあ。
最後に「(7) 平方根」です。
Busicom-141PF-Calculator_asm_rel-1-0-1.txtには、"Square root implementation"という記述があり、なにやら複雑な計算方法の説明と疑似コードが載っているのですが、四則演算が出来るならニュートン法で計算できるよね?と思い、ニュートン法を使った計算を実装してみました。ニュートン法による開平計算の漸化式は
X_i+1 = (X_i + A/X_i)/2
のように書けます。
逆ポーランド記法でスタックが4段あれば、この式は
0.5 ↑ X ↑ A ↑ X / + *
又は、
2 ↑ X ↑ A ↑ X / + /
のようにかなり簡単に書けます。今回の実装では2で割るより0.5を掛ける方がたぶん速いので上の方を採用しました。
(3)~(6)の四則演算ルーチンをちゃんとしたサブルーチンに整備したり、逆ポーランドのスタックを4段に拡張したり、若干の修正が必要でしたが比較的簡単に実装できました。
これで電卓作りの目標にしていたsqrt(sqrt(2143/22))(円周率の近似値)の計算が出来ました。
次は言語的なものを実装してマンデルブロ集合を計算させようと思っています。マンデルブロ集合の計算だけなら機械語で書く方が簡単だろうけど、できれば高級言語で実装したいな。





























 (3)
(3)