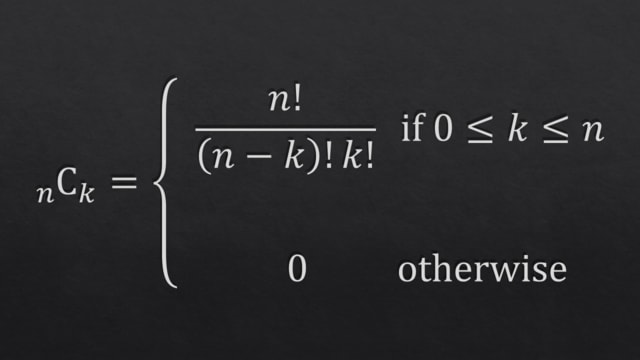先日の記事では,"乗法公式" を用いて【二項係数の漸化式】を導きました:

今回は,同じ恒等式を【組合せ】のアイディアに基づいて導いてみたいと思います:
直感的なので個人的にはお気に入りの証明です.
次回は,「二項展開における係数」という本来の【二項係数】の定義に従って,母関数の考え方で別証明を試みたいと思います!
注1.【組合せの総数】と【二項係数の関係】
(0) nCk は,「異なるn個のものからk個を選ぶ方法の総数」(k-組合せの総数)を表します.
(1) (1+ X)^n を二項展開した際の X^k の項の係数を「二項係数」と言い,nCkと一致します.
(2) したがって,組合せの総数と二項係数を同一視できます.
注2.(再掲)集合の考え方に基づく【組合せ】の定義
(3) S を濃度が n (⋖ ∞) の集合とします(つまり要素が n 個の有限集合とします).
(4) 組合せ論では, S の部分集合のうち濃度が k であるものを「S の k-組合せ」と呼びます.
(5) またS の k-組合せ全体から成る集合を P_k(S) と書くとき,この集合の濃度 |P_k(S)| を nCk と表記します.